


The two techniques discussed provided most of the existing data on the Sunyaev-Zel'dovich effect until very recently. Both techniques are excellent for large-scale surveys of clusters of galaxies which are well matched to the beam-switching technique being used, but provide only modest angular resolutions on the sky (although higher-resolution and two-dimensional bolometer arrays are now becoming available) and hence are suitable only for simple mapping (as in Figs. 17 and 19). Radio interferometry is a powerful method for making detailed images of Sunyaev-Zel'dovich effects. Such images are valuable for making detailed comparisons with X-ray images, and can also measure accurate Sunyaev-Zel'dovich effects while avoiding some of the systematic difficulties of the other techniques. Perhaps for these reasons, interferometry is the most rapidly-growing area for observation of the Sunyaev-Zel'dovich effects (Table 3).
| Paper | 
|  p p
| B | Telescope |
| (GHz) | (arcmin) | (m) | ||
| Partridge et al. 1987 | 4.9 | 9 | 35-1030 | VLA |
| Jones et al. 1993 | 15 | 6 | 18- 108 | RT |
| Grainge et al. 1993 | 15 | 6 | 18- 108 | RT |
| Jones 1995 | 15 | 6 | 18- 108 | RT |
| Saunders 1995 | 15 | 6 | 18- 108 | RT |
| Liang 1995 | 8.8 | 5 | 31- 153 | ATCA |
| Carlstrom et al. 1996 | 29 | 4 | 20- 75 | OVMMA |
| Grainge 1996 | 15 | 6 | 18- 288 | RT |
| Grainge et al. 1996 | 15 | 6 | 18- 288 | RT |
| Jones et al. 1997 | 15 | 6 | 18- 108 | RT |
| Matsuura et al. 1996 | 15 | 6 | 18- 108 | RT |
Note. -  is the central
frequency of observation. is the central
frequency of observation.  p is the corresponding FWHM of the beam
provided by the primary antennas of the interferometer. B is the
range of baselines that were used in the work.
The telescopes are the Very Large Array (VLA), Ryle
Telescope (RT), Australia Telescope Compact Array (ATCA), and Owens
Valley Radio Observatory Millimeter Array (OVMMA). p is the corresponding FWHM of the beam
provided by the primary antennas of the interferometer. B is the
range of baselines that were used in the work.
The telescopes are the Very Large Array (VLA), Ryle
Telescope (RT), Australia Telescope Compact Array (ATCA), and Owens
Valley Radio Observatory Millimeter Array (OVMMA).
| ||||
The extra resolution that is available using interferometers is also a handicap. Interferometers work by measuring some range of Fourier components of the brightness distribution on the sky: the correlation of signals from a pair of antennas produces a response which is (roughly) proportional to a single Fourier component of the brightness of the source. For ``small'' sources, observed with narrow bandwidths and short time constants, the measured source visibility is
where B(
Most interferometers were originally designed to achieve high angular
resolution. The finiteness of interferometer measurements means that
not all (u,v) values are sampled: in particular, the design for high
resolution means that the antennas are usually placed so that their
minimum separation is many wavelengths (and always exceeds the antenna
diameter by a significant factor). The Fourier relationship
(92) means that the short baselines contain
information about the large angular scale structure of the source, and
so there is some maximum angular scale of structure that is sampled
and imaged by interferometers. The Sunyaev-Zel'dovich effects of clusters of
galaxies have angular sizes of several arcminutes - most
interferometers lose (``resolve out'') signals on these or larger
angular scales, and hence would find extreme difficulty in detecting
Sunyaev-Zel'dovich effects.
Figure 21 illustrates this effect for model Very
Large Array (VLA) observations of cluster CL 0016+16 at
Smaller interferometers would allow the Sunyaev-Zel'dovich effects to be
measured. What is needed is an array of antennas whose individual
beam-sizes are significantly larger than the angular sizes of the
cluster Sunyaev-Zel'dovich effects, so that many antenna-antenna
baselines can be
arranged to be sensitive to the effects. A first attempt to customize
a telescope for this experiment was the upgrade of the 5-km
telescope at Cambridge, UK into the Ryle telescope
(Birkinshaw & Gull
1983b;
Saunders 1995).
In its new configuration, the five central
12.8-m diameter antennas can occupy a number of parking points which
provide baselines from 18 m to 288 m. At the prime operating
wavelength of 2 cm, the maximum detectable Sunyaev-Zel'dovich effect signal is
about -1.3 mJy, and several baselines should see effects in excess
of -0.1 mJy.
The choice of operating wavelength for mapping the Sunyaev-Zel'dovich effect is
constrained to some extent by confusion, in the same way that the
radiometric observations are affected. Some clusters of
galaxies (particularly clusters of galaxies with strong Sunyaev-Zel'dovich
effects;
Moffet & Birkinshaw
1989)
contain cluster halo sources, with similar angular size to the cluster
as a whole and whose non-thermal radio emission can swamp the
Sunyaev-Zel'dovich effects at low
frequencies (although their non-thermal Sunyaev-Zel'dovich effects are probably
small; Sec. 5). Such sources
have steep spectra, and so are avoided by working at higher
frequencies. Clusters of galaxies also contain a population of radio
sources, many of which are extended (the wide angle tail sources,
narrow angle tail sources, etc.). These extended sources are also
avoided by working at high frequency, where their extended emission is
minimized and where the small-scale emission can be recognized by its
different range of Fourier components. Background, flat-spectrum,
radio sources can also affect the data, but can be
recognized by their small angular size.
Interferometers with a wide range of baselines are useful in this
respect: the longer baselines are sensitive to the small-angular scale
radio sources which dominate the radio confusion signal (and which
affect the radiometric data: see
Fig. 15), while the shorter
baselines contain both the radio source signal and the
Sunyaev-Zel'dovich effect
signal. Thus the longer-baseline data can be analysed first to locate
the confusing radio sources, and then these sources can be subtracted
from the short-baseline data, so that a source-free map of the sky can
be constructed and searched for the Sunyaev-Zel'dovich effect. Furthermore, by
tuning the range of baselines that are included in the final map, or
by appropriately weighting these baselines, a range of image
resolutions can be produced to emphasize any of a range of angular
structures.
Of course, this technique depends on there being a good separation of
angular scales between the radio sources and the Sunyaev-Zel'dovich
effects in the
clusters: extended, cluster-based, radio sources cannot be removed
reliably using this technique, and there are a number of clusters in
which no good measurements of (or limits to) the Sunyaev-Zel'dovich
effects can be obtained without working at a higher frequency with a smaller
interferometer (to avoid resolving out the Sunyaev-Zel'dovich effect). A
good choice
of operating frequency might be 90 GHz, with antenna baselines of a
few metres: a design which also commends itself for imaging primordial
fluctuations in the background radiation.
Since many of the brightest radio sources at the frequencies for which
interferometers are used are variable (with timescales of months being
typical), the subtraction technique must sometimes be applied to
individual observing runs on a cluster, rather than to all the data
taken together. The brightest sources may also subtract imperfectly
because of dynamic range problems in the mapping and analysis of the
data: generally interferometric or radiometric observations of
clusters are only attempted if the radio source environment is
relatively benign. Any source contamination at a level
Although the interferometric technique is extremely powerful, in
taking account of much of the radio source confusion, and in allowing
a map of the Sunyaev-Zel'dovich effect to be constructed, it does suffer
from some
new difficulties of its own. First, the range of baselines over which
the Sunyaev-Zel'dovich effect is detected may be highly restricted, so that the
``map'' is little more than an indication of the location of the most
compact component of the Sunyaev-Zel'dovich effects. This problem can
only be solved
by obtaining more short baselines, which may not be possible because
of excessive antenna size (as with the VLA, for example).
The source subtraction may also cause problems, since strong sources
outside the target clusters
often lie towards the edges of the primary beam of the antennas of the
interferometer. Small pointing errors in the antennas can then cause
the amplitude of these sources to modulate significantly, adding to
the noise in the map and reducing the accuracy with which the
contaminating source signal can be removed from the Sunyaev-Zel'dovich effect.
The problem is worst for sources lying near the half-power point
of the primary beam, but significant difficulties can be caused by
sources lying even in distant sidelobes, although this extra noise
does not usually add to produce a coherent contaminating signal at the
map center, where the Sunyaev-Zel'dovich effect is normally expected.
Careful attention must also be paid to the question of correlator
errors, which can produce large and spurious signals near the
phase-stopping center (see
Partridge et
al. 1987).
In order to avoid
excessive bandwidth smearing for contaminating sources which must be
identified and removed successfully, it is also normal to observe using
bandwidth synthesis methods (which split the continuum bandpass of the
interferometer into a number of channels). The combination of these
individual channel datasets back into a continuum map of the Sunyaev-Zel'dovich
effect may sometimes be complicated by steep (or strongly-inverted)
sources on the image which have different fluxes in the
different channels.
One major advantage of using an interferometer is that the effects of
structures in the atmosphere are significantly reduced. Emission from
the atmosphere is important only in its contribution to the total noise power
entering the antennas, since this emission is uncorrelated over
baselines longer than a few metres and does not enter into the
(correlated) visibility data. Furthermore, there are no background
level problems: an interferometer does not respond to a constant
background level, and so a well-designed interferometer will not
respond to constant atmospheric signals, the uniform component of the
microwave background radiation, large-scale gradients in galactic
continuum emission, or ground emission entering through the telescope
sidelobes.
The first cluster for which interferometric techniques were used
successfully is Abell 2218, which had been shown to have a strong
Sunyaev-Zel'dovich
effect with a small angular size using single-dish measurements
(Birkinshaw, Gull &
Hardebeck 1984).
Jones et al.
(1993)
used the Ryle interferometer at 15 GHz, with baselines
from 18 to 108 m, to locate sources and to map the diffuse
Sunyaev-Zel'dovich effect. The images that they obtained are shown in
Fig. 22. Using baselines from 36 to 108 m, and 27
12-hour runs, a high signal/noise map of the cluster radio sources was
made (Fig. 22, left). Using only the 18-m baseline,
and subtracting the signals from
these sources, a map with effective angular resolution about 2 arcmin
was then made (Fig. 22, right). This clearly shows a
significant negative signal, of
-580 ± 110 µJy, centered at
16h 35m 47s +66° 12' 50" (J2000). The
corresponding value for the central Sunyaev-Zel'dovich effect in the
cluster cannot
be determined without knowing the shape of the efficiency curve
(e.g., Fig. 21, which is effectively a visibility
curve) on baselines
less than those that were observed. The Ryle interferometer data
could be fitted with models of the form (66), with a
parameter space extending from
Much analysis of the Sunyaev-Zel'dovich effect can usefully be carried
out in the data, rather than the map, plane - by fitting the model
V(u,v) to the measured
visibilities. Indeed, the most
reliable indication of the reality of a Sunyaev-Zel'dovich effect may be its
presence first in visibility plots (like Fig. 21),
and such plots are invaluable for assessing the extent of the missing
visibility data in (u,v), and hence the fraction of the full
Sunyaev-Zel'dovich
effect of a cluster that is being detected by the interferometer. Of
course, similar calculations are needed for radiometric and bolometric
observations of the Sunyaev-Zel'dovich effects, but the efficiency
factors
More recently, excellent imaging data on the clusters CL 0016+16 and
Abell 773 has been published by
Carlstrom et al. (1996).
These authors used the Owens Valley Millimeter Array (OVMMA) at 1 cm: by
equipping an array designed for operation at 3 mm and shorter
wavelengths with cm-wave receivers, they were assured of
accurate pointing and a relatively large primary beam, so that the
interferometer should not over-resolve the Sunyaev-Zel'dovich effects on short
baselines. The total negative flux
density of CL 0016+16 in this operating configuration is near -13 mJy
if the cluster has a central decrement of -1 mK,
so that the cluster should be relatively strong (negative) source. With the
OVMMA,
Carlstrom et
al. (1996)
detected a total negative flux density
of -3.0 mJy after 13 days of observation: their map of the cluster
is shown in Fig. 23.
The power of radio interferometric mapping of a cluster is apparent in
Carlstrom et al.'s map of
the Sunyaev-Zel'dovich effect from CL 0016+16. The Sunyaev-Zel'dovich decrement
is extended in the same position angle as the X-ray
emission (Fig. 2)
and the distribution of optical galaxies (and close to the
position angle from the cluster to a companion cluster;
Hughes et al. 1995).
The small-scale structure seen in this
image is close to that predicted from the X-ray image, and corresponds
closely with the predicted amplitude based on earlier radiometric
detections of the Sunyaev-Zel'dovich effect of the cluster
(Uson 1986;
Birkinshaw 1991).
The success of recent interferometric mapping campaigns, which have
produced results such as Fig. 24 has
amply justified demonstrated the potential
of this technique to improve on single-dish
observations of the Sunyaev-Zel'dovich effect. The critical elements of this
breakthrough have been the development of small interferometers
dedicated to Sunyaev-Zel'dovich effect mapping over long intervals, and the
existence of stable, low-noise receivers with exceptionally wide
passbands.
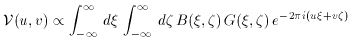
 ,
,  ) is the brightness
distribution of the sky,
G(
) is the brightness
distribution of the sky,
G( ,
,  ) represents the polar
diagram of the antennas of the
interferometer, (u,v) are the separations of the antennas, measured
in wavelengths, (
) represents the polar
diagram of the antennas of the
interferometer, (u,v) are the separations of the antennas, measured
in wavelengths, ( ,
,  ) are direction cosines
relative to the
center of the field of view, and the constant of proportionality
depends on the detailed properties of the interferometer (see
Thompson et al. (1986)
for a detailed
explanation of the meaning of this expression and the assumptions that
go into it). An image of the sky brightness distribution,
B(
) are direction cosines
relative to the
center of the field of view, and the constant of proportionality
depends on the detailed properties of the interferometer (see
Thompson et al. (1986)
for a detailed
explanation of the meaning of this expression and the assumptions that
go into it). An image of the sky brightness distribution,
B( ,
,  ), can be recovered from
the measurements
V(u,v), by a back Fourier
transform and division by the polar
diagram function: alternatively, estimation techniques can be used to
measure B(
), can be recovered from
the measurements
V(u,v), by a back Fourier
transform and division by the polar
diagram function: alternatively, estimation techniques can be used to
measure B( ,
,  ) directly from the
V(u,v).
) directly from the
V(u,v).
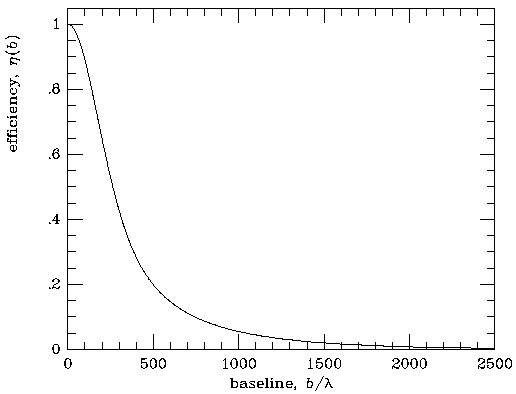
Figure 21. The interferometer response that
would be expected from a 6-cm VLA observation of the Sunyaev-Zel'dovich
effect from
cluster CL 0016+16, normalized to the effect with zero baseline. The
minimum separation of VLA antennas is 650 wavelengths, but projection
effects mean that the minimum observable baseline is roughly equal to
the antenna diameter, or about 420 wavelengths. Thus on the shortest
one or two baselines, for a brief interval, the VLA can observe about
25 per cent of the total available Sunyaev-Zel'dovich effect (which
corresponds to
about -0.9 mJy if the central Sunyaev-Zel'dovich effect is about -1 mK).
Consequently, the VLA is a poor
instrument for observing the Sunyaev-Zel'dovich effect in this cluster.
 = 6 cm. Since the VLA antennas shadow one another at baselines less
than the antenna diameter (of 25 m), no information about the
amplitude or shape of the
visibility curve can be recovered at baselines less than
420
= 6 cm. Since the VLA antennas shadow one another at baselines less
than the antenna diameter (of 25 m), no information about the
amplitude or shape of the
visibility curve can be recovered at baselines less than
420 . Most of the VLA baselines are much larger than the
minimum baseline, even in the most compact configuration
(D array). Hence the VLA's effective sensitivity to the
Sunyaev-Zel'dovich effect in
CL 0016+16 is low. But CL 0016+16 is a cluster at redshift 0.5455,
has a small angular size, and so represents one of the best candidate
clusters for observation with the VLA - the VLA is therefore not a
useful instrument for measuring the Sunyaev-Zel'dovich effects of any clusters
unless those clusters contain significant small-scale substructure in
the Sunyaev-Zel'dovich effect, or the clusters can have significantly smaller
angular sizes and substantial Sunyaev-Zel'dovich effects.
Thus, for example, the VLA observations of
Partridge et
al. (1987)
suffered from this effect: in their data
the Sunyaev-Zel'dovich effect signal from Abell 2218 was strongly suppressed because of
the excessive size of the array.
. Most of the VLA baselines are much larger than the
minimum baseline, even in the most compact configuration
(D array). Hence the VLA's effective sensitivity to the
Sunyaev-Zel'dovich effect in
CL 0016+16 is low. But CL 0016+16 is a cluster at redshift 0.5455,
has a small angular size, and so represents one of the best candidate
clusters for observation with the VLA - the VLA is therefore not a
useful instrument for measuring the Sunyaev-Zel'dovich effects of any clusters
unless those clusters contain significant small-scale substructure in
the Sunyaev-Zel'dovich effect, or the clusters can have significantly smaller
angular sizes and substantial Sunyaev-Zel'dovich effects.
Thus, for example, the VLA observations of
Partridge et
al. (1987)
suffered from this effect: in their data
the Sunyaev-Zel'dovich effect signal from Abell 2218 was strongly suppressed because of
the excessive size of the array.
 10 mJy is likely to be excessive, and to cause difficulties in
detecting the Sunyaev-Zel'dovich effects, let alone mapping them reliably.
Nevertheless, interferometric work has the advantage over radiometric
work that the sources (in particular the variable, and hence small
angular size sources) are monitored simultaneously with the Sunyaev-Zel'dovich
effect, and so interferometer maps should show much better source
subtraction.
10 mJy is likely to be excessive, and to cause difficulties in
detecting the Sunyaev-Zel'dovich effects, let alone mapping them reliably.
Nevertheless, interferometric work has the advantage over radiometric
work that the sources (in particular the variable, and hence small
angular size sources) are monitored simultaneously with the Sunyaev-Zel'dovich
effect, and so interferometer maps should show much better source
subtraction.

 0.6,
0.6,  c
c
 0.9 arcmin,
0.9 arcmin,
 T0
T0
 -1.1 mK, to
-1.1 mK, to

 1.5,
1.5,
 c
c
 2.0 arcmin,
2.0 arcmin,
 T0
T0
 -0.6 mK. The random error on the
detection of an Sunyaev-Zel'dovich effect is, therefore, much smaller than the
systematic error in
the central measurement of the effect - a better range of baselines,
and a detection of the Sunyaev-Zel'dovich effect on more than a single
baseline, would be needed to improve this situation.
-0.6 mK. The random error on the
detection of an Sunyaev-Zel'dovich effect is, therefore, much smaller than the
systematic error in
the central measurement of the effect - a better range of baselines,
and a detection of the Sunyaev-Zel'dovich effect on more than a single
baseline, would be needed to improve this situation.
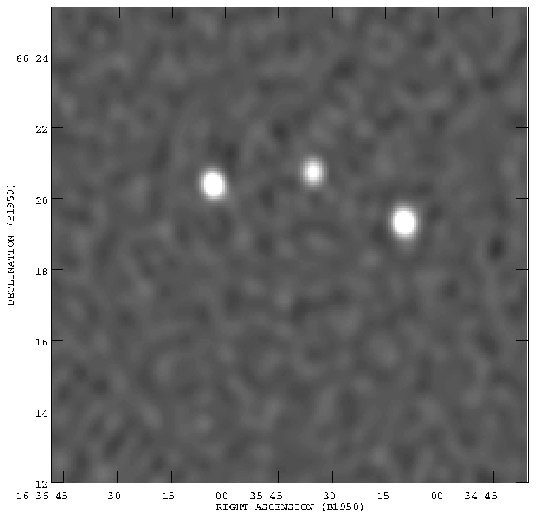
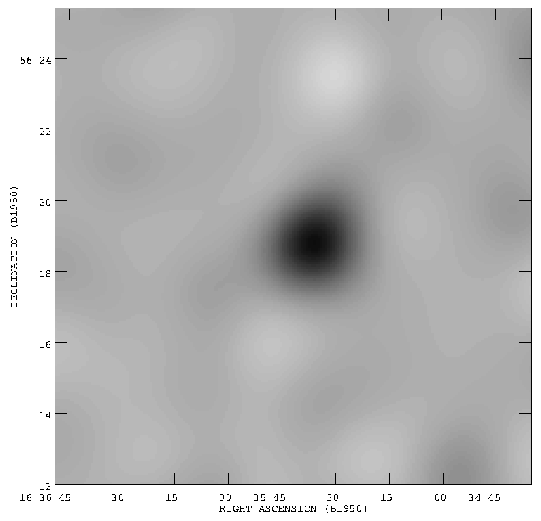
Figure 22. Interferometric maps of Abell 2218, made
with the Ryle telescope of the Mullard Radio Astronomy
Observatory
(Jones et al.
1993).
Left: an image made with the longer-baseline
data, which is sensitive chiefly to small angular scales. Three faint
radio sources dominate the image. Right: an image made with the
short-baseline data, after subtraction of the sources detected on the
long-baseline image. Here the image is dominated by the
Sunyaev-Zel'dovich effect from the cluster.
 (b)
are often lower in interferometric work, and so the sampling of the
full Sunyaev-Zel'dovich effect is more critical to its interpretation.
(b)
are often lower in interferometric work, and so the sampling of the
full Sunyaev-Zel'dovich effect is more critical to its interpretation.
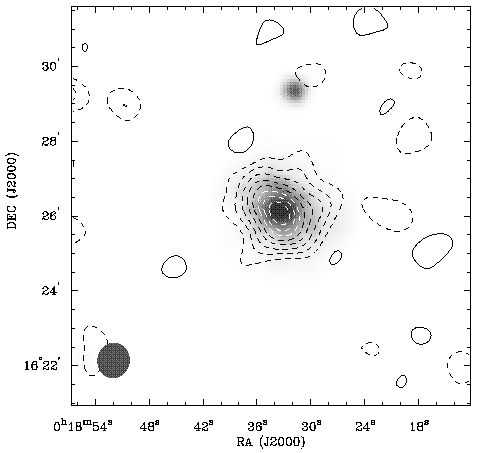
Figure 23. An interferometric map of CL 0016+16,
from
Carlstrom et al. (1996),
superimposed on a grey-scale
representation of the X-ray emission of the cluster (from the ROSAT
PSPC). The radio data on which this image is based
were taken with the Owens Valley Radio Observatory Millimeter Array
operated at 1 cm, contain antenna baselines from 20 to 75 m, and have
a synthesized beam of about 55 arcsec (as shown in the lower left
corner).
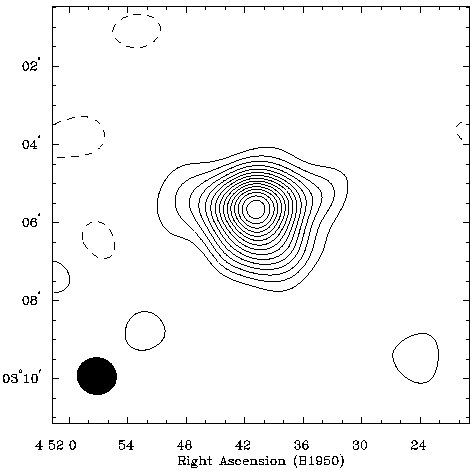
Figure 24. An image of the Sunyaev-Zel'dovich effect from the
cluster MS 0451.6-0305 at
z = 0.55, as measured by Joy et al. (in preparation) using
the OVMMA. The
beamshape of the image is shown in the lower left
corner. This cluster was first detected in the Einstein
Medium-Sensitivity Survey
(Gioia et al. 1990b),
and therefore can be
regarded as a part of an X-ray complete sample.