


The techniques discussed in Section 8 have been
used to search for the
thermal and kinematic Sunyaev-Zel'dovich effects towards a large number
of clusters, and the non-thermal Sunyaev-Zel'dovich effects towards a
few radio galaxies. Over
the past few years this work has been increasingly successful, because
of the high sensitivity that is now being achieved, and the careful
controls on systematic errors that are used by all groups. The most
impressive results are those obtained from radio interferometers,
which are producing images of the cluster Sunyaev-Zel'dovich effects
that can be
compared directly with images of cluster X-ray structures. In the
present section I collect all published results on Sunyaev-Zel'dovich
effects of which I am aware, and review the reliability of the measurements.
9.1.
Cluster data
Table 4 contains the final
result measured in each series of observations for each of the
clusters that has been observed in the Sunyaev-Zel'dovich effect. Not all
papers in Tables 1,
2, and
3 are represented in
Table 4, since
I have excluded interim reports where they have been superseded by later
work (which often involves improved calibrations and assessments of
systematic errors). The column marked ``O/C'' reports whether the
quoted value of  TRJ is as observed or as deconvolved, by
the observers, into some central estimated Sunyaev-Zel'dovich effect. As
explained in
Secs 8.2 and 8.3,
model-fitting to produce a
central decrement is commonly used when only a small fraction of the
central decrement can be recorded by the telescope.
TRJ is as observed or as deconvolved, by
the observers, into some central estimated Sunyaev-Zel'dovich effect. As
explained in
Secs 8.2 and 8.3,
model-fitting to produce a
central decrement is commonly used when only a small fraction of the
central decrement can be recorded by the telescope.
The overall set of clusters for which Sunyaev-Zel'dovich effects have been sought does not constitute a well-defined sample in any sense. Early work on the Sunyaev-Zel'dovich effects concentrated on clusters with strong X-ray sources, or for which the radio source contamination was known to be small. Abell 426 (the Perseus cluster) is an example of a cluster observed for the first reason, despite its strong radio sources (Lake & Partridge 1980). Abell 665, on the other hand, was observed principally because it was known to be largely free of strong radio sources, but also because it is the richest cluster in the Abell catalogue (Birkinshaw et al. 1978a). With more sensitive X-ray surveys, X-ray images, and X-ray spectroscopy, several clusters with exceptional X-ray properties have also been observed. Examples are the high-luminosity cluster CL 0016+16 (Birkinshaw et al. 1981a), and the high-temperature cluster Abell 2163 (Holzapfel et al. 1997b).
More recently, there has been some effort to observe complete samples of clusters of galaxies selected on the basis of their X-ray or optical properties, since the interpretation of cluster Sunyaev-Zel'dovich effects in cosmological terms may be biased by the use of the ad hoc samples that have been assembled to date. Initial steps in these directions have been taken by, for example, Myers et al. (1997). At present, though, it is not possible to use the sample of clusters contained in Table 4 to make reliable statistical statements about the effects of clusters on the CMBR. Attempts to normalize a Sunyaev-Zel'dovich effect cluster luminosity function (e.g., Bartlett & Silk 1994a) based on these clusters may not be safe.
Extreme care is needed in interpreting the results given in this
table. First, the datum that is recorded,  TRJ, is the
measured Sunyaev-Zel'dovich effect from the cited paper at the most significant
level observed (code O), or the central Sunyaev-Zel'dovich effect in the
cluster,
as fitted based on some model of the cluster gas (code C), and which
would be seen in the Rayleigh-Jeans limit if the cluster were observed
with infinitely good angular resolution. That is, for C codes,
TRJ, is the
measured Sunyaev-Zel'dovich effect from the cited paper at the most significant
level observed (code O), or the central Sunyaev-Zel'dovich effect in the
cluster,
as fitted based on some model of the cluster gas (code C), and which
would be seen in the Rayleigh-Jeans limit if the cluster were observed
with infinitely good angular resolution. That is, for C codes,
It is not simple to convert from the measured effects to the central
effects, since proper account must be taken of the method used to
observe the cluster and the efficiency factor
Many of the observations made with bolometers express their results in
terms of y0, the central value of y through the target
cluster. In those cases (e.g.,
Holzapfel et
al. 1997b),
I have converted the results to central decrements using
(93). In cases where the peak beam-averaged
value of
For the interferometric data, the measured flux densities on
the most appropriate (usually lowest-resolution) maps have been
converted into measured brightness temperatures using the synthesized
beamsize quoted. That is, it is assumed that the synthesized beam is
an elliptical Gaussian, with solid angle
which in convenient units, becomes (95)
In the case of the
Partridge et
al. (1987)
data, I
have estimated the error on the central Sunyaev-Zel'dovich effect from their
visibility curves, taking rough account of the systematic errors in
the data caused by correlator offsets.
For the radiometric results, which are the bulk of the entries in
Table 4, the values of
In many cases the radiometric data have been adjusted for the effects
of cluster and background radio sources. These adjustments are not
necessarily consistent between the different papers: as further radio
work has been done on the clusters, some have shown that substantial
radio source corrections are needed (see, for example,
Abell 2507). Sometimes the detections of these radio
sources led to
the cluster observations being abandoned (e.g., for Abell 426). For
other clusters, later work may have used better source corrections and
is often more reliable on these grounds alone. Many of the clusters
with radiometric Sunyaev-Zel'dovich results reported here have had
little supporting work on the radio source environment. This makes it
difficult to assess the extent to which the results are affected by
radio source contamination.
A number of trends are clear in Table 4. Early
observations were dominated by single-dish radiometers (e.g.,
Birkinshaw et
al. 1981b).
More recently, the bolometric technique has been used, specially because of the
interest in detecting the effect near 190 GHz, where the kinematic
effect is more obvious (e.g.,
Holzapfel et
al. 1997b).
Finally, the completion of the Ryle array and the use of the
OVMMA and
BIMA for
Sunyaev-Zel'dovich effect measurements has produced a
series of sensitive maps of clusters (e.g.,
Jones et al.
1993;
Carlstrom et
al. 1996),
where some evidence of the cluster structure is seen (e.g., for CL 0016+16;
Carlstrom et
al. 1996;
Sec. 8.3).
Despite the increasing use of these new techniques, single-dish
radiometry is still used - principally for survey work,
to locate target clusters with significant Sunyaev-Zel'dovich effects
that might be
the subjects of detailed mapping later. Thus observations at OVRO
with the 40-m telescope at present are concentrating on a sample of
clusters selected because of their excellent exposures by the ROSAT PSPC.
Myers et al.
(1997)
are making a survey of another sample of clusters with the OVRO 5.5-m
telescope.
The results in Table 4 span more than 20 years of work
on the Sunyaev-Zel'dovich effect, and involve a number of different
techniques with
different observing characteristics. Thus it is difficult to compare
the results of different groups for any one cluster without taking
detailed account of the structure of the cluster and the details of
the method used. This causes the apparent disagreements between
different groups' results to be accentuated. Nevertheless, there are
clusters for which the data (particularly the more recent data) are
largely in agreement, and clusters for which the situation is less clear.
Consider, for example, the cluster Abell 2218, for which a
particularly large number of measurements are available. First,
consider the history of results for Abell 2218 obtained by the group
with which I have been working. The published results from 1976 to
1996 are given in Table 5. These results are not
independent: later results from the Chilbolton 25-m telescope included
the data used in earlier papers, and the OVRO 40-m results
also changed as more data were accumulated, and as the radio source
corrections and data calibrations were better understood.
The internal consistency of the early data is clearly poor. The final
result based on the Chilbolton data is only marginally consistent
with the first published result, suggesting that the
later data were quite inconsistent with the earlier data. Since a
number of changes in the configuration of the Chilbolton system
occurred during the period that data were taken, it is likely
that this inconsistency arose from unrecognized systematic
errors, possibly involving strong ground signals entering through
distant sidelobes.
Later data, from the OVRO 40-m telescope, appear more consistent -
the 10.7-GHz result and the 20.3-GHz results seem to be indicating
that the value of
If it is assumed that the atmosphere of Abell 2218 follows the model
(64), and is isothermal, then the structural parameters
Another effect that can be seen in Table 5 is
the strong variation in the errors quoted for the 20.3-GHz data as a
function of time. The smallest error (± 0.03 mK, in
Birkinshaw & Moffet 1986)
represents the error on the data
accumulated at that time if all the data are considered to be drawn
from a single, static, Gaussian distribution. The largest error, ±
0.13 mK, in
Birkinshaw & Gull (1984),
is based on the
smallest amount of data, under the same assumptions. On the other hand, the
entry for
Birkinshaw (1986)
is based on substantially
more data than in
Birkinshaw & Moffet
(1986),
but
includes a generous allocation for possible systematic errors. Later
entries in the Table include further data, and were derived with
detailed analyses for systematic errors. It should be noted that the
final result in the table, -0.40 ± 0.05 mK, contains no
contribution from the background CMBR anisotropies, so that the error
represents the reproducibility of the measurement rather than the
external error that would be achieved if Abell 2218 could be observed
against another patch of the background radiation.
Of course, Table 5 illustrates principally the
difficulty in measuring the Sunyaev-Zel'dovich effect signals in the
presence of
systematic errors with unknown characteristics: reductions in the error are
principally achieved by stronger controls against
systematic errors (for example by observing multiple regions of blank
sky, performing checks for radio source contamination, and so
on). More rigorous controls against systematic error are obtained by
comparing the results from different groups who observe the same
cluster in different ways. The most frequently-observed cluster is
Abell 2218, and Table 6 lists the central
decrements for Abell 2218 deduced from 16 independent measurements
using the same model atmosphere as in discussion of
Table 5.
It is at once apparent from Table 6 that the
individual results are inconsistent: the early data are often
scattered with dispersion
several times their nominal error about the later data. In some of the
early papers, large parasitic signals from ground spillover have been
removed (e.g.,
Perrenod & Lada 1979),
but there
remains a suspicion that residual systematic errors are present in the
data. Overall, the later data are in much better agreement. A notable
exception is the result of
Klein et al.
(1991),
where
the measured decrement is consistent with predictions based on other
data, but its location on the sky is far from the X-ray center of the
cluster so that the implied central decrement in Table 6 is
unrealistically large. If an average is taken over these data, and the most
obviously discordant results are excluded, then the central decrement in
Abell 2218 is found to be -0.74 ± 0.07 mK. The error here has been
increased to take some crude account of the remaining discordance in
the data (the value of
The Sunyaev-Zel'dovich effect results for Abell 2218 are generally in better
agreement now than they were for the first few years of reported
measurements. This suggests that several groups are now able to
measure reliable Sunyaev-Zel'dovich effects, and based on this
conclusion, I have collected into Table 7 the set of
all Sunyaev-Zel'dovich effects that I believe are both significant (at
> 4
Detections at lower significance exist for more objects, including the
lines of sight towards two high-redshift quasars (PHL 957,
Andernach et al.
1986;
PC 1643+4631,
Jones et al.
1997).
These detections may
arise from distant clusters of galaxies along the lines of sight, or
from the host clusters of the quasars themselves, or from some other
cause. However, if the Sunyaev-Zel'dovich effects arise from
line-of-sight objects,
then observations towards ``blank'' sky regions should show Sunyaev-Zel'dovich
effects as often as observations towards the quasars - it is not yet
clear whether this is the case, so the interpretation of these
Sunyaev-Zel'dovich effects and the limits from observations of other quasars
(Jones et al.
1997)
or blank fields
(Richards et
al. 1997)
is at present obscure.
Further complications in the interpretation of these results have
arisen as deep optical and X-ray followups have been made. Thus for
the PC 1643+4631 field,
Saunders et al.
(1997)
find no
cluster that might be responsible for a Sunyaev-Zel'dovich effect in
deep optical images, and Kneissl, Sunyaev & White (1998) find no
X-ray emission associated
with hot gas. The interpretation of the CMBR anisotropy as a
Sunyaev-Zel'dovich
effect has become difficult because of the high redshift needed for a
relatively massive cluster that could hold a detectable amount of hot
gas
(Bartlett et al. 1998).
Alternative models involving kinematic effects from colliding
QSO winds
(Natarayan &
Sigurdsson 1997),
extreme Rees-Sciama effects, etc. are being considered, but seem
implausible. Independent observational confirmation of the reality of
these microwave background structures is therefore a priority: early
results are yielding a mixed verdict.
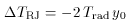
 (see
Fig. 14, for example). For some
observations, for
example with multichannel bolometer systems, it may have been
necessary for the observers to undertake a significant fitting
exercise to extract the central
(see
Fig. 14, for example). For some
observations, for
example with multichannel bolometer systems, it may have been
necessary for the observers to undertake a significant fitting
exercise to extract the central  TRJ,
TRJ,  TRJ0, with the result
depending on the model of the cluster gas adopted
(Sec. 8.2). Clusters with only poor X-ray images are
therefore difficult to assess, but in cases in which there is good
X-ray data this fitting step is relatively reliable. Thus it can be
shown, for example, that recent results for Abell 2218 are in much
better agreement than is apparent from Table 4 (see
later).
TRJ0, with the result
depending on the model of the cluster gas adopted
(Sec. 8.2). Clusters with only poor X-ray images are
therefore difficult to assess, but in cases in which there is good
X-ray data this fitting step is relatively reliable. Thus it can be
shown, for example, that recent results for Abell 2218 are in much
better agreement than is apparent from Table 4 (see
later).
 TRJ
is stated (e.g.,
Chase et al.
1987),
that value is preferred in the table.
TRJ
is stated (e.g.,
Chase et al.
1987),
that value is preferred in the table.
 ab (calculated from the full widths to
half-maximum in two directions, h a x
h b), and the brightness temperature is obtained from
ab (calculated from the full widths to
half-maximum in two directions, h a x
h b), and the brightness temperature is obtained from
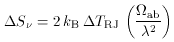
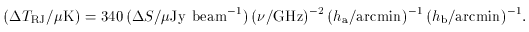
 TRJ are taken
directly from the papers. The results from
Rudnick (1978)
are given
for a 2-arcmin FWHM structure at the cluster center, since this is the
closest match to the resolution of the telescope used. Rudnick also
quotes more sensitive results for
TRJ are taken
directly from the papers. The results from
Rudnick (1978)
are given
for a 2-arcmin FWHM structure at the cluster center, since this is the
closest match to the resolution of the telescope used. Rudnick also
quotes more sensitive results for  TRJ at a number of larger
angular scales by convolving the data. These larger scales may be more
appropriate for some clusters.
TRJ at a number of larger
angular scales by convolving the data. These larger scales may be more
appropriate for some clusters.
 TRJ (mK)
TRJ (mK)
Reference
Telescope; frequency
-1.94 ± 0.54
Gull & Northover
1976
Chilbolton 25-m; 10.6 GHz
-1.09 ± 0.28
Birkinshaw et
al. 1978a
Chilbolton 25-m; 10.6 GHz
-1.49 ± 0.23
Birkinshaw et
al. 1978b
Chilbolton 25-m; 10.6 GHz
-1.05 ± 0.21
Birkinshaw et
al. 1981b
Chilbolton 25-m; 10.6 GHz
-0.38 ± 0.19
Birkinshaw & Gull
1984
OVRO 40-m;
10.7 GHz
-0.34 ± 0.05
Birkinshaw et
al. 1984
OVRO 40-m;
20.3 GHz
-0.31 ± 0.13
Birkinshaw & Gull
1984
OVRO 40-m;
20.3 GHz
-0.39 ± 0.03
Birkinshaw &
Moffet 1986
OVRO 40-m;
20.3 GHz
-0.36 ± 0.10
Birkinshaw 1986
OVRO 40-m;
20.3 GHz
-0.35 ± 0.09
Birkinshaw 1990
OVRO 40-m;
20.3 GHz
-0.40 ± 0.05
Birkinshaw et
al. 1998
OVRO 40-m;
20.3 GHz
 TRJ towards the center of the cluster is about
-0.35 mK. However, the observing characteristics of these
observations was very different, and the low-significant detection at
10.7 GHz is due almost completely to a correction for contaminating
radio sources near the center of the cluster.
TRJ towards the center of the cluster is about
-0.35 mK. However, the observing characteristics of these
observations was very different, and the low-significant detection at
10.7 GHz is due almost completely to a correction for contaminating
radio sources near the center of the cluster.
 = 0.65 ± 0.05
and
= 0.65 ± 0.05
and  c = 1.0 ±
0.1 arcmin derived from X-ray observations
(Birkinshaw & Hughes
1994)
may be used to calculate the efficiencies with which the cluster was observed
by any telescope. For observations of the Sunyaev-Zel'dovich effect of
Abell 2218
with the Chilbolton 25-m telescope, the OVRO 40-m
telescope at 10.7 GHz, and the OVRO 40-m telescope at 20.3 GHz, these efficiencies
are about 0.35, 0.49, and 0.60, respectively. The inferred
central Sunyaev-Zel'dovich effects from the cluster according to the
final results
from these three telescope configurations are therefore -3.0 ±
0.6, -0.77 ± 0.38, and -0.67 ± 0.08 mK. The result from the
Chilbolton 25-m telescope is clearly inconsistent
with the other two
measurements. Only a very contrived structure for the cluster
atmosphere could cause such differences and be consistent with the
other Sunyaev-Zel'dovich effect data and the X-ray image and spectrum. Thus an
economical assumption is that the early data were badly contaminated
by systematic errors, and should be discarded, and that the true
central decrement from Abell 2218 is near -0.7 mK.
c = 1.0 ±
0.1 arcmin derived from X-ray observations
(Birkinshaw & Hughes
1994)
may be used to calculate the efficiencies with which the cluster was observed
by any telescope. For observations of the Sunyaev-Zel'dovich effect of
Abell 2218
with the Chilbolton 25-m telescope, the OVRO 40-m
telescope at 10.7 GHz, and the OVRO 40-m telescope at 20.3 GHz, these efficiencies
are about 0.35, 0.49, and 0.60, respectively. The inferred
central Sunyaev-Zel'dovich effects from the cluster according to the
final results
from these three telescope configurations are therefore -3.0 ±
0.6, -0.77 ± 0.38, and -0.67 ± 0.08 mK. The result from the
Chilbolton 25-m telescope is clearly inconsistent
with the other two
measurements. Only a very contrived structure for the cluster
atmosphere could cause such differences and be consistent with the
other Sunyaev-Zel'dovich effect data and the X-ray image and spectrum. Thus an
economical assumption is that the early data were badly contaminated
by systematic errors, and should be discarded, and that the true
central decrement from Abell 2218 is near -0.7 mK.
 TRJ0 (mK)
TRJ0 (mK)
Reference
-2.6 ± 1.2
Perrenod & Lada
1979
+2.2 ± 1.1
Lake & Partridge
1980
-3.04 ± 0.61
Birkinshaw et
al. 1981b
-4.49 ± 0.80
Schallwich 1982
+0.8 ± 2.4
Lasenby & Davies
1983
-0.77 ± 0.38
Birkinshaw & Gull
1984
-0.48 ± 0.39
Uson 1985
+7.8 ± 5.3
Radford et
al. 1986
+0.21 ± 0.57
Radford et
al. 1986
+0.46 ± 0.36
Radford et
al. 1986
+0.40 ± 0.70
Partridge et
al. 1987
-3.2 ± 1.1
Klein et
al. 1991
-0.90 ± 0.10
Jones 1995
-0.88 ± 0.26
Uyaniker et
al. 1997
-0.67 ± 0.08
Birkinshaw 1998
-0.68 ± 0.19
Tsuboi et
al. 1998
 2
= 15 with 10 degrees of freedom).
2
= 15 with 10 degrees of freedom).
Cluster
Recent measurement
Independent confirmation
Abell 478
Myers et
al. 1997
. . .
Abell 665
Birkinshaw et
al. 1998
Grainge 1996
Abell 697
Grainge 1996
. . .
Abell 773
Carlstrom et
al. 1996
Grainge et
al. 1993
Abell 990
Grainge et
al. 1996
. . .
Abell 1413
Grainge et
al. 1996
. . .
Abell 1656
Herbig et
al. 1995
. . .
Abell 1689
Holzapfel et
al. 1997b
. . .
Abell 2142
Myers et
al. 1997
. . .
Abell 2163
Holzapfel et
al. 1997b
. . .
Abell 2218
Birkinshaw et
al. 1998
Jones 1995
Abell 2256
Myers et
al. 1997
. . .
CL 0016+16
Carlstrom et
al. 1996
Birkinshaw et
al. 1998
 )
and reliable. These objects constitute a set for which a simultaneous
analysis of the Sunyaev-Zel'dovich effect data and the X-ray data may
provide useful constraints on the cluster atmospheres
(Sec. 10), and
possibly a measurement of the Hubble constant
(Sec. 11). Of the thirteen clusters in the
table, seven were first detected using single-dish radiometers,
two using bolometers, and four using interferometers. Only four of
these detections have independent confirmations at significance >
4
)
and reliable. These objects constitute a set for which a simultaneous
analysis of the Sunyaev-Zel'dovich effect data and the X-ray data may
provide useful constraints on the cluster atmospheres
(Sec. 10), and
possibly a measurement of the Hubble constant
(Sec. 11). Of the thirteen clusters in the
table, seven were first detected using single-dish radiometers,
two using bolometers, and four using interferometers. Only four of
these detections have independent confirmations at significance >
4 . Much work remains to be done
to measure the Sunyaev-Zel'dovich effects in
these clusters, and all three measurement techniques still have their
place in Sunyaev-Zel'dovich effect research, although bolometer
measurements are becoming more important, and interferometric maps of
the effect are probably the most reliable.
. Much work remains to be done
to measure the Sunyaev-Zel'dovich effects in
these clusters, and all three measurement techniques still have their
place in Sunyaev-Zel'dovich effect research, although bolometer
measurements are becoming more important, and interferometric maps of
the effect are probably the most reliable.