


Only McKinnon et al. (1990) have yet made direct attempts to measure the non-thermal Sunyaev-Zel'dovich effect, and their results are reported in Table 8.
| Object | Redshift |  TRJ (mK) TRJ (mK)
| Reference |
| 0742+318 | 0.462 | +0.25 ± 0.59 | McKinnon 1990 |
| 1721+343 | 0.206 | +0.05 ± 1.08 | McKinnon et al. 1990 |
| 2221-02 | 0.057 | -1.74 ± 0.76 | McKinnon et al. 1990 |
| 2349+32 | 0.671 | +1.18 ± 0.91 | McKinnon et al. 1990 |
As explained in Sec. 5, the aim of observations of the non-thermal Sunyaev-Zel'dovich effect is to set limits on the electron population in radio source lobes. The constraints that McKinnon et al. (1990) derived based on the data in Table 8 are far (two orders of magnitude) from achieving this aim. With the best techniques available, it should be possible to improve the sensitivity by roughly a factor of 10 over McKinnon et al.'s results in a modest allocation of observing time: a further improvement would be gained by working on radio sources with steep spectra and for which the telescope beam is a small fraction of the radio source size.
Perhaps the best possibility of effecting these improvements is with modern bolometer arrays, observing radio sources with large lobes and sufficiently steep radio spectra that radio emission is not an issue. In view of the possible impact on radio source theory, such observations should certainly be attempted.
Beam-filling non-thermal Sunyaev-Zel'dovich effects may already have been observed, however, as part of the signals from some clusters of galaxies. In the Coma cluster, for example, Herbig et al. (1995) detected a strong Sunyaev-Zel'dovich effect, but a bright radio halo source is known to exist (Hanisch 1982; Kim et al. 1990), and it may be responsible for some part of the observed signal if the relativistic electron population has a significant lower-energy component. Another case where this is true is Abell 2163, where a strong Sunyaev-Zel'dovich effect has been measured (Holzapfel et al. 1997a), and a powerful radio halo source exists (Herbig & Birkinshaw 1998). However, if we attempt to interpret the results for Abell 2163 in terms of a contamination of the measured Sunyaev-Zel'dovich effect by a non-thermal component, we rapidly recognize that the non-thermal Sunyaev-Zel'dovich effect is principally a test of the lower energy cutoff of the power-law distribution of electrons responsible for the radio halo source's synchrotron emission rather than of equipartition. Roughly,
which depends strongly on the lower Lorentz factor cutoff of the
electron spectrum,
Thus although the sizes of the non-thermal effects from radio halo
sources are likely to be a small fraction of the thermal
effects, they may exert an interesting influence on the
spectrum of the combined signal by shifting the location of
the zero of the spectrum away from the location expected on the basis
of the thermal and velocity effects alone, if the spectrum of
relativistic electrons in the cluster extends down to moderate Lorentz
factors. This non-thermal Sunyaev-Zel'dovich effect is a source of
systematic error that should be considered when
measuring cluster peculiar velocities, and argues that several
spectral bands, and detailed spectral fitting, are required to set
rigorous limits to cluster velocities.
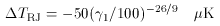
 1 (and weakly on the value of the Hubble
constant). If we assume that about half the central Sunyaev-Zel'dovich
effect (of -1.62 ± 0.22 mK;
Holzapfel et
al. 1997b)
is produced by this non-thermal process, then
1 (and weakly on the value of the Hubble
constant). If we assume that about half the central Sunyaev-Zel'dovich
effect (of -1.62 ± 0.22 mK;
Holzapfel et
al. 1997b)
is produced by this non-thermal process, then  1
1  30. This
corresponds to the radio-emitting plasma in the cluster contributing a
small fraction of the gas pressure (if the radio source is close to
equipartition). However, a non-thermal Sunyaev-Zel'dovich effect of this
size would
have a severe effect on the location of the zero of the spectrum of
the combined thermal, kinematic, and non-thermal effects from the
cluster, and
Holzapfel et
al. (1997b)
find that the
spectrum shows no signature of a cluster peculiar velocity, and hence
no zero shift. Since
30. This
corresponds to the radio-emitting plasma in the cluster contributing a
small fraction of the gas pressure (if the radio source is close to
equipartition). However, a non-thermal Sunyaev-Zel'dovich effect of this
size would
have a severe effect on the location of the zero of the spectrum of
the combined thermal, kinematic, and non-thermal effects from the
cluster, and
Holzapfel et
al. (1997b)
find that the
spectrum shows no signature of a cluster peculiar velocity, and hence
no zero shift. Since  1 depends on
1 depends on  TRJ only weakly,
changing the fraction of the central
TRJ only weakly,
changing the fraction of the central  TRJ to ensure consistency
with Holzapfel et al. results in a limit
TRJ to ensure consistency
with Holzapfel et al. results in a limit  1
1  50 which
is little changed from the value above. An even higher value for
50 which
is little changed from the value above. An even higher value for
 1 is
likely, since low-energy electrons
suffer rapid ionization losses
(Rephaeli & Silk 1995),
and might not be expected to be present unless there is a fast
local acceleration mechanism.
1 is
likely, since low-energy electrons
suffer rapid ionization losses
(Rephaeli & Silk 1995),
and might not be expected to be present unless there is a fast
local acceleration mechanism.