


The Sunyaev-Zel'dovich effects provide a window on cluster properties which differs significantly from that afforded by optical, X-ray, or conventional radio data. The present section of this review concentrates on these implications of the measurement of the effects for the understanding of cluster properties.
10.1.
Cluster gas properties
The original purpose of measuring the Sunyaev-Zel'dovich effects of clusters was to test whether cluster X-ray emission was thermal in origin, or came from non-thermal processes such as inverse-Compton emission from relativistic electrons and the cosmic background radiation (e.g., Harris & Romanishin 1974). This use of the effects was rapidly made moot by the detection of line emission from clusters of galaxies (e.g., Serlemitsos et al. 1977).
Until recently there were few high-sensitivity measurements of the Sunyaev-Zel'dovich effects from clusters, so that little information could be obtained that was not already available from X-ray images and spectra. Thus, for example, the structural information from cluster Sunyaev-Zel'dovich effects based on radiometric data (e.g., Fig. 17) has much lower signal/noise than the X-ray images of those same clusters (e.g., Fig. 2). This is less true with imaging of the quality that should be available from interferometers, but at present interferometers measure only a fraction of the Fourier information needed for a full reconstruction of the microwave background structure generated by clusters of galaxies, and hence model-fitting to these interferometer images is usually based on existing X-ray data (see Sec. 8.3).
The Sunyaev-Zel'dovich effects do differ significantly from the X-ray data in their sensitivity to different properties of the atmospheres. If a cluster is at rest in the Hubble flow, then in the non-relativistic limit the low-frequency, thermal, Sunyaev-Zel'dovich effect from that cluster on a particular line of sight is
where y is the Comptonization parameter, which depends on
the line-of-sight electron density and temperature as
(62), and is thus proportional to the line-of-sight
integral of the electron pressure.
By contrast, the X-ray surface brightness on that
line of sight depends on these same quantities as
(63), where
Once again, this has largely been superseded by improvements in X-ray
technology. The newer generation of X-ray observatories provides
some spatially-resolved X-ray spectra of clusters
of galaxies and hence direct measurements of
variations in the thermal structures of clusters. Sunyaev-Zel'dovich effect
data could still be an important probe of structure in the outer parts of
clusters, since at low densities the Sunyaev-Zel'dovich effect drops off less
rapidly (
The remaining area where information about the Sunyaev-Zel'dovich effect
provides unique information about the structure of the cluster gas is on the
smallest scales, where structures in the X-ray gas are unresolved by
X-ray or radio telescopes. In this case, the structures are better
described by a (possibly position-dependent) clumping of the
gas, and unless the density and temperature changes in the clumps
conspire, the Sunyaev-Zel'dovich effect and X-ray surface
brightness scale differently. For example, if clumping is isobaric,
with the pressure in clumps the same as outside, then the
Sunyaev-Zel'dovich effect
will show no variations in regions where the gas is strongly clumped,
while the X-ray emissivity will increase as
ne3/2. No
useful results on the clumping of cluster gas have been reported in
the literature to date: it is more usual to see clumping referred to
as one of the limiting factors in the use of the Sunyaev-Zel'dovich effects to
measure the Hubble constant
(Sec. 11.1), although
clumping in the intracluster medium is also a biasing factor in the
use of the X-ray data to determine gas densities and masses from X-ray
images and spectra.
A direct use of the thermal Sunyaev-Zel'dovich effect is as a probe of the gas
mass enclosed within the telescope beam
(Myers et al.
1997).
For an isothermal model of the form (64), the
surface mass density in gas along a given line of sight is
where µe is the mean mass of gas per electron,
while the thermal Sunyaev-Zel'dovich effect at low frequency is
proportional to the Comptonization parameter (eq. 98).
Thus the surface mass density in gas can be related to the
Sunyaev-Zel'dovich effect (as measured through the Comptonization
parameter) as
if the electron temperature of the gas is constant.
For clusters such as Abell 2218 which have both a rich population of arcs
(Sarantini et al. 1996)
and a strong
Sunyaev-Zel'dovich effect, the measure (101) of the gas surface density
could be compared directly with mass estimates produced by the
study of gravitational arcs to estimate
the fraction of the lensing mass that is contained in gas. Although
this study is possible using the X-ray emission from a
cluster, X-rays provide a less direct measure of gas mass, being
biased by uncertainties in the clumpiness of the gas. The
Sunyaev-Zel'dovich effect should be less susceptible to errors of
interpretation, and give a clean estimate of the ratio of baryonic and
dark matter within the arcs, which relates to the baryon problem in
clusters
(White & Fabian 1995).
To make the best use of this
comparison, the Sunyaev-Zel'dovich effect data should be taken with resolutions
better than the radii of the gravitational arcs. Unfortunately
observations with high brightness temperature sensitivity and angular
resolutions of 10 arcsec or better are very difficult, and this limits
the utility of this comparison at present.
Myers et al.
(1997)
show that for three clusters of galaxies,
the ratio of baryonic mass to total gravitating mass (here derived not
from gravitational lensing, but rather from cluster dynamics) is in
the range 0.06 h100-1 to 0.17
h100-1. These values are
larger than the baryonic mass fraction (0.013 ± 0.002)
h100-2 expected from calculations of
big-bang nucleosynthesis
if 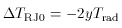
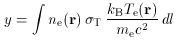
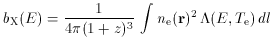
 (E,
Te) is the X-ray spectral
emissivity, which is a function of the energy of the X-ray
observation, E, the electron temperature of the gas,
Te,
the metallicity of the gas, and the redshift, z. The emissivity
depends on temperature roughly as
(E,
Te) is the X-ray spectral
emissivity, which is a function of the energy of the X-ray
observation, E, the electron temperature of the gas,
Te,
the metallicity of the gas, and the redshift, z. The emissivity
depends on temperature roughly as

 Te1/2 if the X-ray pass-band is
sufficiently broad, so that the X-ray
surface brightness is proportional to the line-of-sight integral of
ne2 Te1/2
while the Sunyaev-Zel'dovich effect is proportional to
the line-of-sight integral of ne Te.
The Sunyaev-Zel'dovich effect and X-ray surface
brightness of a cluster of galaxies are then likely to have different angular
structures (if we rule out the possibility of coincidences in the
density and temperature structures), and the
difference between the X-ray and Sunyaev-Zel'dovich effect images should
provide information on the runs of temperature and density in the
cluster gas.
Te1/2 if the X-ray pass-band is
sufficiently broad, so that the X-ray
surface brightness is proportional to the line-of-sight integral of
ne2 Te1/2
while the Sunyaev-Zel'dovich effect is proportional to
the line-of-sight integral of ne Te.
The Sunyaev-Zel'dovich effect and X-ray surface
brightness of a cluster of galaxies are then likely to have different angular
structures (if we rule out the possibility of coincidences in the
density and temperature structures), and the
difference between the X-ray and Sunyaev-Zel'dovich effect images should
provide information on the runs of temperature and density in the
cluster gas.
 ne) than
the X-ray surface brightness (
ne) than
the X-ray surface brightness ( ne2). This region of the gas
distribution might be expected
to show the clearest evidence of deviations from the remarkably
successful isothermal-
ne2). This region of the gas
distribution might be expected
to show the clearest evidence of deviations from the remarkably
successful isothermal- model, but the current sensitivity of
Sunyaev-Zel'dovich effect measurements is too low, relative to the
sensitivity of X-ray images and spectra, for useful comparisons to be made.
Where the cluster contains a radio source (particularly a
radio halo source), the thermal Sunyaev-Zel'dovich effect is of
particular interest
since it provides a direct measurement of the electron pressure near
that radio source, and so can be used to test whether the dynamics of
the radio emitting plasma are strongly affected by the external gas
pressure.
model, but the current sensitivity of
Sunyaev-Zel'dovich effect measurements is too low, relative to the
sensitivity of X-ray images and spectra, for useful comparisons to be made.
Where the cluster contains a radio source (particularly a
radio halo source), the thermal Sunyaev-Zel'dovich effect is of
particular interest
since it provides a direct measurement of the electron pressure near
that radio source, and so can be used to test whether the dynamics of
the radio emitting plasma are strongly affected by the external gas
pressure.
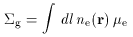
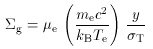
 0 = 1
(Smith et al.
1993).
As a result, we
can infer that the Universe is open, with
0 = 1
(Smith et al.
1993).
As a result, we
can infer that the Universe is open, with  0
0  0.2
h100-1, or that clusters show a baryon
segregation effect, with excess baryons in their X-ray luminous cores
and excess dark matter further out.
0.2
h100-1, or that clusters show a baryon
segregation effect, with excess baryons in their X-ray luminous cores
and excess dark matter further out.