Annu. Rev. Astron. Astrophys. 1992. 30: 311-358 Copyright © 1992 by Annual Reviews. All rights reserved

3.5 Microlensing

For a sufficiently compact source, individual stars in a lensing galaxy can modify the magnification relative to that expected from a smoothly-distributed lens (Bliokh & Minakov 1975, Chang & Refsdal 1979, Gott 1981, Young 1981, Chang 1984, Vietri & Ostriker 1983, Nityananda & Ostriker 1984, Paczynski 1986a). This phenomenon is termed microlensing, in contrast to the effect of the smooth mass distribution which is referred to as macrolensing.

A convenient measure of the influence of an isolated star is its Einstein radius (Equation 4). The optical depth for a source to lie within an Einstein ring is given by = ^*/ _cr, where ^* is the total stellar surface density, and is independent of the masses of the individual stars. When << 1, the faint microimages associated with individual stars are unimportant except on the rare occasions when a star crosses within a few _E of the line of sight. When this happens the source will brighten and fade on a timescale given by

12.

where V is the velocity of the star relative to the source-earth line and D' is given by Equation 7. In contrast to the optical depth, t_var does depend on the mass of the microlens (Kayser et al. 1986, Kayser & Refsdal 1989, Kayser 1992).

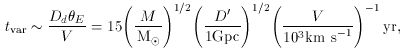
As increases, the microlenses can no longer be considered in isolation. At moderate , the combined, long range action (through shear) of the background stars can be thought of as creating a quadrupole lens at the site of each star (Chang & Refsdal 1984, Nityananda & Ostriker 1984, Lee & Spergel 1990). This can break the circular symmetry and allow slender caustic surfaces to form behind individual stars, leading to extra image pairs. At still higher , when the Einstein rings start to overlap, a complicated caustic network will develop (Schneider & Weiss 1986, Kayser et al. 1989, Wambsganss 1990, Witt 1990). The backgound shear from the largescale mass distribution of the lens makes the network anisotropic and the variability will be sensitive to the direction of transverse motion relative to the shear (Wambsganss 1990, Wambsganss et al. 1990a). Frequent, large amplitude image variation is possible in this regime (Paczynski 1986a, Nemiroff 1986, Schneider & Weiss 1987, Witt 1990). If there is a smooth, supercritical background density, then dramatic demagnifications are also expected when the ray associated with the brightest microimage intercepts a star. The net effect will be to conserve flux so that the mean magnification is the same as if the mass in the stars had been smoothed out (Peacock 1986). Since fold caustics dominate at the highest magnification, the asymptotic probability for large magnification by more than µ scales as µ^-2 (Section 3.3, Vietri & Ostriker 1983, Nityananda & Ostriker 1984, Blandford & Narayan 1986), with a normalization that can be computed exactly (Schneider 1987c). Numerical simulations show a significant excess in the crosssection (over and above the analytical normalization of the µ^-2 law) at moderate magnifications (Rauch et al. 1991).

When a caustic associated with the macroimage is approached, the number of stars contributing to the macroimage as well as the mean magnification increase, rendering numerical simulation impractical (Deguchi & Watson 1987, 1988). For ~ 1, the number of microimages becomes so large that the fluctuation level in fact diminishes. When >> 1, the mean magnification decreases ^-2 again but the relative fluctuations, for fixed source size, are found to increase (Deguchi & Watson 1988). In this limit the angular profile of the macroimage consists of a Gaussian core and a power law tail ^-4 (Katz et al. 1986).

Variability associated with microlensing is strongly attenuated if the angular size of the source becomes comparable to the Einstein radius of the microlenses (e.g. Wambsganss 1992, Refsdal & Stabell 1991). This can be used to set limits on the sizes of emission regions of distant sources (cf Section 6.1).

Irwin et al. (1989) and Corrigan et al. (1991) have reported variability in the images of Q2237+031. Since the optical depth for microlensing in this case is ~ 0.5, the variations have been plausibly interpreted as being the result of microlensing. Schild & Smith (1991) appear to have measured variability due to microlensing in Q0957+561.