


1.2 Introducing the cosmological constant
Einstein's original field equations are
(I use conventions in which c = 1, and will also set
where d
The energy-momentum sources may be modeled as a perfect fluid,
specified by an energy density
where Uµ is the fluid four-velocity.
To obtain a Robertson-Walker solution to Einstein's equations,
the rest frame of the fluid must be that of a comoving observer
in the metric (2); in that case, Einstein's
equations reduce to the two Friedmann equations
where we have introduced the Hubble parameter
H
Einstein was interested in finding static
(
where
and
These equations admit a static solution with positive spatial
curvature and all the parameters
The discovery by Hubble that the universe is expanding eliminated
the empirical need for a static world model (although the
Einstein static universe continues to thrive in the toolboxes
of theorists, as a crucial step in the construction of conformal
diagrams). It has also been criticized on the grounds that
any small deviation from a perfect balance between the
terms in (9) will rapidly grow into a runaway
departure from the static solution.
Pandora's box, however, is not so easily closed. The
disappearance of the original motivation for introducing the
cosmological constant did not change its status as a
legitimate addition to the gravitational field equations,
or as a parameter to be constrained
by observation. The only way to purge
1 This account gives
short shrift to the details of what actually happened;
for historical background see
[10].
Back.
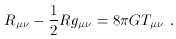
 = 1
in most of the formulae to follow, but Newton's constant
will be kept explicit.) On very large scales the universe is
spatially homogeneous
and isotropic to an excellent approximation, which implies that
its metric takes the Robertson-Walker form
= 1
in most of the formulae to follow, but Newton's constant
will be kept explicit.) On very large scales the universe is
spatially homogeneous
and isotropic to an excellent approximation, which implies that
its metric takes the Robertson-Walker form
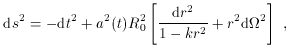
 2 =
d
2 =
d 2 +
sin2
2 +
sin2 d
d
 2 is the metric on a
two-sphere. The curvature parameter
k takes on values +1, 0, or -1 for positively curved,
flat, and negatively curved spatial sections, respectively.
The scale factor characterizes the relative size of the
spatial sections as a function of time; we have written it in
a normalized form a(t) = R(t) / R0, where
the subscript 0 will always refer to a quantity evaluated
at the present time.
The redshift z undergone by radiation from a comoving object
as it travels to us today is related to the scale factor
at which it was emitted by
2 is the metric on a
two-sphere. The curvature parameter
k takes on values +1, 0, or -1 for positively curved,
flat, and negatively curved spatial sections, respectively.
The scale factor characterizes the relative size of the
spatial sections as a function of time; we have written it in
a normalized form a(t) = R(t) / R0, where
the subscript 0 will always refer to a quantity evaluated
at the present time.
The redshift z undergone by radiation from a comoving object
as it travels to us today is related to the scale factor
at which it was emitted by
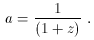
 and isotropic
pressure p
in its rest frame. The energy-momentum tensor of such a fluid
is
and isotropic
pressure p
in its rest frame. The energy-momentum tensor of such a fluid
is
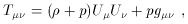
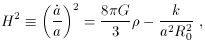

 / a, and
/ a, and
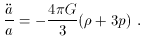
 = 0)
solutions, both due to his hope that general relativity would
embody Mach's principle that matter determines inertia,
and simply to account for the astronomical data as they
were understood at the time.
(1)
A static universe
with a positive energy density is compatible with
(5) if the spatial curvature is positive (k = +1)
and the density is appropriately tuned; however,
(6) implies that
= 0)
solutions, both due to his hope that general relativity would
embody Mach's principle that matter determines inertia,
and simply to account for the astronomical data as they
were understood at the time.
(1)
A static universe
with a positive energy density is compatible with
(5) if the spatial curvature is positive (k = +1)
and the density is appropriately tuned; however,
(6) implies that 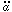 will never vanish in
such a spacetime if the pressure p is also nonnegative
(which is true for most forms of matter, and certainly
for ordinary sources such as stars and gas). Einstein
therefore proposed a modification of his equations, to
will never vanish in
such a spacetime if the pressure p is also nonnegative
(which is true for most forms of matter, and certainly
for ordinary sources such as stars and gas). Einstein
therefore proposed a modification of his equations, to
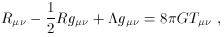
 is a new free
parameter, the cosmological constant. Indeed, the left-hand side of (7)
is the most general local, coordinate-invariant,
divergenceless, symmetric, two-index tensor we can
construct solely from the metric and its first and second
derivatives. With this modification, the Friedmann
equations become
is a new free
parameter, the cosmological constant. Indeed, the left-hand side of (7)
is the most general local, coordinate-invariant,
divergenceless, symmetric, two-index tensor we can
construct solely from the metric and its first and second
derivatives. With this modification, the Friedmann
equations become
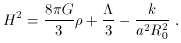
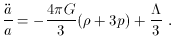
 , p, and
, p, and
 nonnegative. This solution is called the ``Einstein static
universe."
nonnegative. This solution is called the ``Einstein static
universe."
 from
cosmological discourse would be to measure all of the
other terms in (8) to sufficient precision
to be able to conclude that the
from
cosmological discourse would be to measure all of the
other terms in (8) to sufficient precision
to be able to conclude that the
 /3
term is negligibly small in comparison, a feat which has
to date been out of reach. As discussed below, there
is better reason than ever before to believe that
/3
term is negligibly small in comparison, a feat which has
to date been out of reach. As discussed below, there
is better reason than ever before to believe that
 is actually nonzero, and
Einstein may not have blundered after all.
is actually nonzero, and
Einstein may not have blundered after all.