


2.2 Model universes and their fates
In the remainder of this section we will explore the behavior
of universes dominated by matter and vacuum energy,
 =
=
 M +
M +

 = 1 -
= 1 -
 k. According to
(32), a positive cosmological constant accelerates the
universal expansion, while a negative cosmological constant
and/or ordinary matter tend to decelerate it. The relative
contributions of these components change with time; according
to (28) we have
k. According to
(32), a positive cosmological constant accelerates the
universal expansion, while a negative cosmological constant
and/or ordinary matter tend to decelerate it. The relative
contributions of these components change with time; according
to (28) we have
For
Given
Conversely, if the cosmological constant is sufficiently large
compared to the matter density, the universe has always been
accelerating, and rather than a Big Bang its early history
consisted of a period of gradually slowing contraction to a
minimum radius before beginning its current expansion. The
criterion for there to have been no singularity in the past is
where ``coss'' represents cosh when
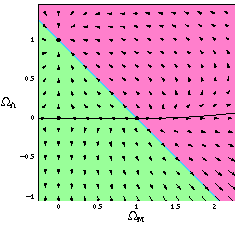
The dynamics of universes with
Figure 1. Dynamics for
This is not a true phase-space plot, despite the superficial
similarities. One important difference is that a universe passing
through one point can pass through the same point again but moving
backwards along its trajectory, by first going to infinity and
then turning around (recollapse).
Figure (1) includes three fixed points, at
(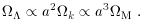

 < 0, the universe will
always recollapse to a Big Crunch,
either because there is a sufficiently high matter density or
due to the eventual domination of the negative cosmological constant.
For
< 0, the universe will
always recollapse to a Big Crunch,
either because there is a sufficiently high matter density or
due to the eventual domination of the negative cosmological constant.
For 
 > 0 the universe will
expand forever unless
there is sufficient matter to cause recollapse before
> 0 the universe will
expand forever unless
there is sufficient matter to cause recollapse before

 becomes dynamically
important. For
becomes dynamically
important. For

 = 0 we have the familiar
situation in which
= 0 we have the familiar
situation in which
 M
M
 1 universes expand forever and
1 universes expand forever and
 M > 1 universes
recollapse; notice, however, that
in the presence of a cosmological constant there is no necessary
relationship between spatial curvature and the fate of the universe.
(Furthermore, we cannot reliably determine that the universe will
expand forever by any set of measurements of
M > 1 universes
recollapse; notice, however, that
in the presence of a cosmological constant there is no necessary
relationship between spatial curvature and the fate of the universe.
(Furthermore, we cannot reliably determine that the universe will
expand forever by any set of measurements of

 and
and
 M; even if we seem
to live in a parameter space
that predicts eternal expansion, there is always the possibility
of a future phase transition which could change the equation of
state of one or more of the components.)
M; even if we seem
to live in a parameter space
that predicts eternal expansion, there is always the possibility
of a future phase transition which could change the equation of
state of one or more of the components.)
 M, the value of
M, the value of

 for which
the universe will expand forever is given by
for which
the universe will expand forever is given by
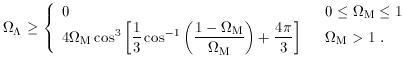
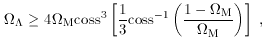
 M < 1/2, and
cos when
M < 1/2, and
cos when  M > 1/2.
M > 1/2.
 =
=
 M +
M +

 are summarized in
Figure (1), in
which the arrows indicate the evolution of these parameters in
an expanding universe. (In a contracting universe they would
be reversed.)
are summarized in
Figure (1), in
which the arrows indicate the evolution of these parameters in
an expanding universe. (In a contracting universe they would
be reversed.)
 =
=
 M +
M +

 .
The arrows indicate the direction of evolution of the
parameters in an expanding universe.
.
The arrows indicate the direction of evolution of the
parameters in an expanding universe.
 M,
M,

 ) equal to (0, 0), (0, 1),
and (1, 0). The attractor among these at (1, 0) is known
as de~Sitter space - a universe with no matter density, dominated
by a cosmological constant, and with scale factor growing
exponentially with time. The fact that this point is an attractor
on the diagram is another way of understanding the cosmological
constant problem. A universe with initial conditions located
at a generic point on the diagram will, after several expansion
times, flow to de Sitter space if it began above the recollapse
line, and flow to infinity and back to recollapse if it began
below that line. Since our universe has undergone a large
number of e-folds of expansion since early times, it must
have begun at a non-generic point in order not to have evolved
either to de Sitter space or to a Big Crunch. The only other
two fixed points on the diagram are the saddle point at
(
) equal to (0, 0), (0, 1),
and (1, 0). The attractor among these at (1, 0) is known
as de~Sitter space - a universe with no matter density, dominated
by a cosmological constant, and with scale factor growing
exponentially with time. The fact that this point is an attractor
on the diagram is another way of understanding the cosmological
constant problem. A universe with initial conditions located
at a generic point on the diagram will, after several expansion
times, flow to de Sitter space if it began above the recollapse
line, and flow to infinity and back to recollapse if it began
below that line. Since our universe has undergone a large
number of e-folds of expansion since early times, it must
have begun at a non-generic point in order not to have evolved
either to de Sitter space or to a Big Crunch. The only other
two fixed points on the diagram are the saddle point at
( M,
M,

 ) = (0, 0), corresponding
to an empty universe, and the repulsive fixed point at
(
) = (0, 0), corresponding
to an empty universe, and the repulsive fixed point at
( M,
M,

 ) = (1, 0), known as the
Einstein-de~Sitter solution. Since our universe is not empty,
the favored solution from this combination of theoretical and
empirical arguments is the Einstein-de~Sitter universe.
The inflationary scenario
[21,
22,
23] provides a
mechanism whereby the universe can be driven to the line
) = (1, 0), known as the
Einstein-de~Sitter solution. Since our universe is not empty,
the favored solution from this combination of theoretical and
empirical arguments is the Einstein-de~Sitter universe.
The inflationary scenario
[21,
22,
23] provides a
mechanism whereby the universe can be driven to the line
 M
+
M
+ 
 = 1 (spatial flatness), so
Einstein-de~Sitter is a natural expectation if we imagine that
some unknown mechanism sets
= 1 (spatial flatness), so
Einstein-de~Sitter is a natural expectation if we imagine that
some unknown mechanism sets
 = 0. As discussed below,
the observationally favored universe is located on this line
but away from the fixed points, near
(
= 0. As discussed below,
the observationally favored universe is located on this line
but away from the fixed points, near
( M,
M,

 ) = (0.3, 0.7). It is
fair to conclude that naturalness arguments have a somewhat
spotty track record at predicting cosmological parameters.
) = (0.3, 0.7). It is
fair to conclude that naturalness arguments have a somewhat
spotty track record at predicting cosmological parameters.