

The fact that galaxies of different types cluster differently [23, 41, 51, 43, 32, 27] implies that many of them are biased tracers of the underlying mass distribution. Without such biasing, it is hard to reconcile the existence of large volumes void of galaxies [38] and the spiky distribution of galaxies on ~ 100 h-1 Mpc scales, today [9] and at high redshifts [56, 55], with the standard theory of gravitational instability theory (GI). There is partial theoretical understanding of the origin of biasing [35, 14, 3, 22, 21, 8, 1, 42, 46], supported by cosmological simulations which confirm the existence of biasing [10, 37, 6, 54] and show that it becomes stronger at high redshifts [2, 34, 59, 54].
The biasing is interesting as a constraint on galaxy formation, but it
is also of great importance when estimating the cosmological density
parameter  . If one assumes
linear and deterministic biasing
and applies the linear approximation for GI,
. If one assumes
linear and deterministic biasing
and applies the linear approximation for GI,  . v = -f(
. v = -f( )
) where f(
where f( )
) 
 0.6
[49], the observables
g and
0.6
[49], the observables
g and  . v are related via the degenerate combination
. v are related via the degenerate combination

 f(
f( ) / b. Thus, one cannot
pretend to have determined
) / b. Thus, one cannot
pretend to have determined
 by measuring
by measuring  without a detailed
knowledge of the biasing scheme.
without a detailed
knowledge of the biasing scheme.
It turns out that different methods lead to different estimates of  in the range 0.4
in the range 0.4 

 1.1
[15,
57,
18,
16].
The methods include:
(a) comparisons of local moments of g (from redshift surveys) and
1.1
[15,
57,
18,
16].
The methods include:
(a) comparisons of local moments of g (from redshift surveys) and
 (from peculiar velocities) or the corresponding power spectra or
correlation functions;
(b) linear regressions of the fields g and
(from peculiar velocities) or the corresponding power spectra or
correlation functions;
(b) linear regressions of the fields g and  , or the corresponding
velocity fields; and
(c) analyses of redshift distortions in redshift surveys.
In order to sharpen our determination of
, or the corresponding
velocity fields; and
(c) analyses of redshift distortions in redshift surveys.
In order to sharpen our determination of  , it is important that
we understand this scatter in
, it is important that
we understand this scatter in  . Some of it is due to the different
types of galaxies involved and some may be due to the effects of
non-linear gravity and perhaps other sources of systematic errors.
Here we investigate the possible contribution of nontrivial properties
of the biasing scheme such as stochasticity and non-linearity.
. Some of it is due to the different
types of galaxies involved and some may be due to the effects of
non-linear gravity and perhaps other sources of systematic errors.
Here we investigate the possible contribution of nontrivial properties
of the biasing scheme such as stochasticity and non-linearity.
The theory of density peaks in a Gaussian random field
[35,
3]
predicts that the linear galaxy-galaxy and mass-mass correlation
functions are related via  gg(r) = b2
gg(r) = b2  mm(r),
where the biasing
parameter b is a constant independent of scale r.
However, a much
more demanding linear biasing model is often assumed, in which the local
density fields are related deterministically via the relation
g(x) = b
mm(r),
where the biasing
parameter b is a constant independent of scale r.
However, a much
more demanding linear biasing model is often assumed, in which the local
density fields are related deterministically via the relation
g(x) = b  (x). This is not a viable model because
(a) it has no theoretical motivation, (b) if b > 1 it must break down
in deep voids because values of g below -1 are forbidden,
and (c) conservation of galaxy number implies that the linear biasing
relation is not preserved during fluctuation growth. Thus, non-linear
biasing, where b varies with
(x). This is not a viable model because
(a) it has no theoretical motivation, (b) if b > 1 it must break down
in deep voids because values of g below -1 are forbidden,
and (c) conservation of galaxy number implies that the linear biasing
relation is not preserved during fluctuation growth. Thus, non-linear
biasing, where b varies with  , is inevitable.
Indeed, the theoretical analysis of the biasing of collapsed halos
by Mo & White
[46],
using the extended Press-Schechter approximation
[7],
predicts that the biasing is non-linear. It provides a
useful approximation for its behavior as a function of scale, time and
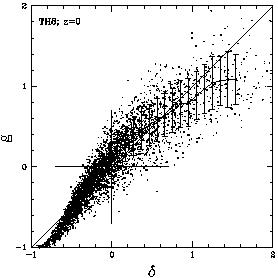
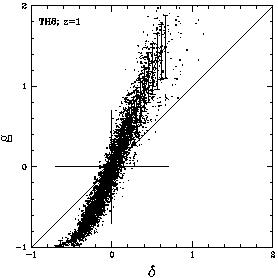
mass. N-body simulations, which provide a more accurate description
(see Figure 1;
[54]),
show that this model is indeed useful.
, is inevitable.
Indeed, the theoretical analysis of the biasing of collapsed halos
by Mo & White
[46],
using the extended Press-Schechter approximation
[7],
predicts that the biasing is non-linear. It provides a
useful approximation for its behavior as a function of scale, time and
mass. N-body simulations, which provide a more accurate description
(see Figure 1;
[54]),
show that this model is indeed useful.
|
|
Figure 1. Biasing of galactic halos versus
mass in a cosmological N-body simulation,
demonstrating non-linearity and stochasticity.
The conditional mean [< g | |
Note that once the biasing is non-linear at one smoothing scale, the
biasing at any other smoothing scale must obey a different functional
form of b( ) and is
non-deterministic. Thus, any deviation from
the simplified linear biasing model must also involve scale-dependence
and scatter. Another inevitable source of scatter is physical scatter
in the efficiency of galaxy formation as a function of
) and is
non-deterministic. Thus, any deviation from
the simplified linear biasing model must also involve scale-dependence
and scatter. Another inevitable source of scatter is physical scatter
in the efficiency of galaxy formation as a function of  ,
because the mass density at a certain smoothing scale (larger than the
scale of galaxies) cannot be the sole quantity determining galaxy formation.
For example, the random variations in the density on smaller scales
and the local geometry of the background structure must play a role too.
These hidden parameters would show up as scatter in the density-density
relation. A third obvious source of scatter is the shot noise. One can
try to remove it a priori, but this is sometimes difficult because of the
small-scale anti-correlations introduced by the finite extent of galaxies.
The alternative is to treat the shot noise as an intrinsic part of the local
stochasticity of the biasing relation. The scatter arising from all the
above is clearly seen for halos in simulations including gravity alone
(Section 4) even before the complex processes of
gas dynamics, star formation and feedback affect the biasing.
,
because the mass density at a certain smoothing scale (larger than the
scale of galaxies) cannot be the sole quantity determining galaxy formation.
For example, the random variations in the density on smaller scales
and the local geometry of the background structure must play a role too.
These hidden parameters would show up as scatter in the density-density
relation. A third obvious source of scatter is the shot noise. One can
try to remove it a priori, but this is sometimes difficult because of the
small-scale anti-correlations introduced by the finite extent of galaxies.
The alternative is to treat the shot noise as an intrinsic part of the local
stochasticity of the biasing relation. The scatter arising from all the
above is clearly seen for halos in simulations including gravity alone
(Section 4) even before the complex processes of
gas dynamics, star formation and feedback affect the biasing.