To appear in Large-Scale Surveys (IAP Symposium XIV,
Paris, France, May 1998),
eds Y. Mellier & S. Colombi (Editions Frontieres).
GALAXY BIASING: NONLINEAR, STOCHASTIC AND MEASURABLE
Avishai Dekel
Racah Institute of
Physics, The Hebrew
University, Jerusalem 91904,
Israel
ABSTRACT. I describe a general formalism for galaxy biasing
[20] and its
application to measurements of β
( Ω0.6 /
b), e.g., via direct comparisons of light and mass and via redshift
distortions. The linear and deterministic relation g = b
δ between the density
fluctuation fields of galaxies g and mass δ is replaced by the
conditional distribution
P(|gδ) of these as random
fields, smoothed at a given scale and at a given time. The mean biasing
and its non-linearity are characterized by the conditional mean
< g|δ >
Ω0.6 /
b), e.g., via direct comparisons of light and mass and via redshift
distortions. The linear and deterministic relation g = b
δ between the density
fluctuation fields of galaxies g and mass δ is replaced by the
conditional distribution
P(|gδ) of these as random
fields, smoothed at a given scale and at a given time. The mean biasing
and its non-linearity are characterized by the conditional mean
< g|δ >  b(δ)
δ, and the local scatter
by the conditional variance
σb2(δ).
This scatter arises from hidden effects on galaxy formation
and from shot noise.
b(δ)
δ, and the local scatter
by the conditional variance
σb2(δ).
This scatter arises from hidden effects on galaxy formation
and from shot noise.
For applications involving second-order local moments, the biasing is
defined by three natural parameters: the slope
 of the regression
of g on δ (replacing
b), a non-linearity parameter
of the regression
of g on δ (replacing
b), a non-linearity parameter
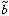 , and a
scatter parameter σb. The ratio
of variances bvar2 and the correlation
coefficient r mix these
parameters. The non-linearity and scatter lead to underestimates of order
, and a
scatter parameter σb. The ratio
of variances bvar2 and the correlation
coefficient r mix these
parameters. The non-linearity and scatter lead to underestimates of order
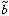 2 /
2 /
 2 and
σb2 /
2 and
σb2 /
 2 in the different
estimators of β,
which may partly explain the range of estimates.
2 in the different
estimators of β,
which may partly explain the range of estimates.
Local stochasticity affects the redshift-distortion analysis only by
limiting the useful range of scales. In this range, for linear
stochastic biasing, the analysis reduces to Kaiser's formula for
 (not bvar) independent of the scatter. The distortion
analysis is
affected by non-linearity but in a weak way.
(not bvar) independent of the scatter. The distortion
analysis is
affected by non-linearity but in a weak way.
Estimates of the nontrivial features of the biasing scheme are made based
on simulations
[54]
and toy models, and a new method for measuring
them via distribution functions is proposed
[53].
Table of Contents

 Ω0.6 /
b), e.g., via direct comparisons of light and mass and via redshift
distortions. The linear and deterministic relation g = b
δ between the density
fluctuation fields of galaxies g and mass δ is replaced by the
conditional distribution
P(|gδ) of these as random
fields, smoothed at a given scale and at a given time. The mean biasing
and its non-linearity are characterized by the conditional mean
< g|δ >
Ω0.6 /
b), e.g., via direct comparisons of light and mass and via redshift
distortions. The linear and deterministic relation g = b
δ between the density
fluctuation fields of galaxies g and mass δ is replaced by the
conditional distribution
P(|gδ) of these as random
fields, smoothed at a given scale and at a given time. The mean biasing
and its non-linearity are characterized by the conditional mean
< g|δ >  b(δ)
δ, and the local scatter
by the conditional variance
σb2(δ).
This scatter arises from hidden effects on galaxy formation
and from shot noise.
b(δ)
δ, and the local scatter
by the conditional variance
σb2(δ).
This scatter arises from hidden effects on galaxy formation
and from shot noise.
 of the regression
of g on δ (replacing
b), a non-linearity parameter
of the regression
of g on δ (replacing
b), a non-linearity parameter
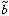 , and a
scatter parameter σb. The ratio
of variances bvar2 and the correlation
coefficient r mix these
parameters. The non-linearity and scatter lead to underestimates of order
, and a
scatter parameter σb. The ratio
of variances bvar2 and the correlation
coefficient r mix these
parameters. The non-linearity and scatter lead to underestimates of order
