


In the scheme outlined above, the function
b( ) contains the
information about the mean biasing (via the parameter
) contains the
information about the mean biasing (via the parameter
 ) and its
non-linear features (e.g., via
) and its
non-linear features (e.g., via
 /
/
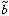 ).
The next quantity of interest in the case of stochastic biasing is
the conditional standard deviation, the function
).
The next quantity of interest in the case of stochastic biasing is
the conditional standard deviation, the function
 b(
b( ),
and its variance over
),
and its variance over  ,
,
 b2.
In order to evaluate the actual effects of non-linear and stochastic
biasing on the various measurements of
b2.
In order to evaluate the actual effects of non-linear and stochastic
biasing on the various measurements of
 , one should try
to evaluate these functions or parameters
from simulations, theoretical approximations and observations.
, one should try
to evaluate these functions or parameters
from simulations, theoretical approximations and observations.
In an ongoing study that generalizes earlier investigations
[10,
46],
we are investigating the biasing in high-resolution
N-body simulations of several cosmological scenarios, both for galactic
halos and for galaxies as identified using semi-analytic models
[54].
We refer here to a representative cosmological model:
 = 1 with a
= 1 with a
 CDM power spectrum which roughly obeys
the constraints from large-scale structure.
The simulation mass resolution is 2 x 1010
M
CDM power spectrum which roughly obeys
the constraints from large-scale structure.
The simulation mass resolution is 2 x 1010
M inside a box
of comoving side 85 h-1 Mpc. The present epoch is
identified with
inside a box
of comoving side 85 h-1 Mpc. The present epoch is
identified with
 8 = 0.6.
Figure 1
demonstrates the qualitative features of the biasing scheme.
The non-linear behavior at
8 = 0.6.
Figure 1
demonstrates the qualitative features of the biasing scheme.
The non-linear behavior at  < 1
is characteristic
of all masses, times, and smoothing scales:
b(
< 1
is characteristic
of all masses, times, and smoothing scales:
b( ) << 1 near
) << 1 near
 = -1 and it
steepens to b(
= -1 and it
steepens to b( ) > 1 towards
) > 1 towards
 = 0.
At
= 0.
At  > 1
the behavior strongly depends on the mass, time
and smoothing scale.
The scatter in the figure includes both shot noise and physical scatter
which are hard to separate properly.
In the case shown at z = 0, the non-linear parameter is
> 1
the behavior strongly depends on the mass, time
and smoothing scale.
The scatter in the figure includes both shot noise and physical scatter
which are hard to separate properly.
In the case shown at z = 0, the non-linear parameter is
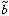 2 /
2 /
 2 = 1.08,
and the scatter parameter is
2 = 1.08,
and the scatter parameter is
 b2 /
b2 /
 2 = 0.15.
The effects of stochasticity and non-linearity in this specific
case thus lead to moderate differences in the various measures of
2 = 0.15.
The effects of stochasticity and non-linearity in this specific
case thus lead to moderate differences in the various measures of
 , on the order of 20-30%.
Gas-dynamics and other non-gravitational processes
may extend the range of estimates even further.
, on the order of 20-30%.
Gas-dynamics and other non-gravitational processes
may extend the range of estimates even further.
Given the distribution
P( ) of the matter fluctuations,
the biasing function b(
) of the matter fluctuations,
the biasing function b( )
should obey by definition at least the following two constrains.
First, g
)
should obey by definition at least the following two constrains.
First, g  -1 everywhere,
because the galaxy density
-1 everywhere,
because the galaxy density  g cannot be negative, with
g = -1 at
g cannot be negative, with
g = -1 at  = -1, because
there are no galaxies where there is no matter. Second,
<g> = 0 because g describes fluctuations about the mean
galaxy density.
An example for a simple functional form that obeys the constraint at
= -1, because
there are no galaxies where there is no matter. Second,
<g> = 0 because g describes fluctuations about the mean
galaxy density.
An example for a simple functional form that obeys the constraint at
 = -1 and reduces to the linear
relation near
= -1 and reduces to the linear
relation near  = 0 is
[17]
= 0 is
[17]
The constraint <g> = 0 is to be enforced by a specific choice of
the factor c for a given b.
With b > 1, this functional form indeed provides a reasonable fit
to the simulated halo biasing relation in the
The non-linear biasing function can alternatively be parameterized by
Since g must average to zero, this general power series can be
written as
where
In order to evaluate the parameters
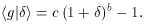
 < 0 regime.
However, the same value of b does not
necessarily fit the biasing relation in the
< 0 regime.
However, the same value of b does not
necessarily fit the biasing relation in the
 > 0 regime.
A better approximation could thus be provided by a combination of two
functions like Eq. (18)
with two different parameters bn and
bp in the regimes
> 0 regime.
A better approximation could thus be provided by a combination of two
functions like Eq. (18)
with two different parameters bn and
bp in the regimes

 0 and
0 and
 > 0 respectively.
The parameter bn is always larger than unity
while bp ranges from slightly below unity to much
above unity.
The best fit to Fig. 1 at z = 0
has bn ~ 2 and bp ~ 1.
At high redshift both bn and bp
become significantly larger.
> 0 respectively.
The parameter bn is always larger than unity
while bp ranges from slightly below unity to much
above unity.
The best fit to Fig. 1 at z = 0
has bn ~ 2 and bp ~ 1.
At high redshift both bn and bp
become significantly larger.
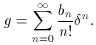
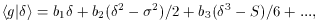
 2
2
 <
< 2>,
S
2>,
S  <
< 3>, etc.
This determines the constant term b0.
The constraint at -1 provides another relation between the parameters.
Therefore, the expansion to third order contains only two free parameters
out of four.
3>, etc.
This determines the constant term b0.
The constraint at -1 provides another relation between the parameters.
Therefore, the expansion to third order contains only two free parameters
out of four.
 and
and
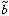 for these non-linear
toy models, we approximate the distribution
P(
for these non-linear
toy models, we approximate the distribution
P( ) as
log-normal in
) as
log-normal in  /
/
 = 1 +
= 1 +
 [12,
39],
where
[12,
39],
where  is the single free parameter.
With Eq. (20), Assuming b2 << b1 and
is the single free parameter.
With Eq. (20), Assuming b2 << b1 and
 << 1, one obtains
<< 1, one obtains
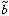 2 /
2 /
 2
2
 1 + (1/2)
(b2 / b1)2
1 + (1/2)
(b2 / b1)2
 2.
This is always larger than unity, but the deviation is small.
Alternatively, using the functional form of Eq. (18), with
bn ranging from 1 to 5 and
bp ranging from 0.5 to 3,
and with
2.
This is always larger than unity, but the deviation is small.
Alternatively, using the functional form of Eq. (18), with
bn ranging from 1 to 5 and
bp ranging from 0.5 to 3,
and with  = 0.7, we find
numerically that
= 0.7, we find
numerically that 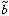 /
/
 is in the range 1.0 to 1.15.
These two toy models, calibrated by
the N-body simulations, indicate that despite the obvious
non-linearity, especially in the negative regime, the non-linear parameter
is in the range 1.0 to 1.15.
These two toy models, calibrated by
the N-body simulations, indicate that despite the obvious
non-linearity, especially in the negative regime, the non-linear parameter
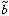 /
/
 is typically only slightly
larger than unity.
This means that the effects of non-linear biasing on measurements of
is typically only slightly
larger than unity.
This means that the effects of non-linear biasing on measurements of
 are likely to be relatively small.
are likely to be relatively small.