


Let  (x) be the
field of mass-density fluctuations and g (x)
the corresponding field of galaxy-density
fluctuations, at a given time and for a given type of object.
The fields are both smoothed with a fixed window
which defines the term ``local''.
The local biasing relation is considered to be
a random process, specified by the
biasing conditional distribution P(g |
(x) be the
field of mass-density fluctuations and g (x)
the corresponding field of galaxy-density
fluctuations, at a given time and for a given type of object.
The fields are both smoothed with a fixed window
which defines the term ``local''.
The local biasing relation is considered to be
a random process, specified by the
biasing conditional distribution P(g |
 ).
Let the one-point probability distribution
functions (PDF) P(
).
Let the one-point probability distribution
functions (PDF) P( ) and
P(g) be of zero means
and standard deviations
) and
P(g) be of zero means
and standard deviations  2
2  <
<  2 > and
2 > and
 g2
g2
 < g2 >.
< g2 >.
Define the mean biasing function b( ) by the conditional
mean,
) by the conditional
mean,
This function is plotted in Figure 1.
It is a natural generalization of the deterministic linear biasing relation,
g = b1
It will become clear that
The local statistical character of the biasing can be expressed
by the conditional moments of higher order about the mean at a given
The scaling by
From the three basic parameters defined above one can derive other
biasing parameters.
A common one is the ratio of variances,
The second equality is a result of Eq. (4).
It immediately shows that bvar is sensitive both to
non-linearity and
to stochasticity, with bvar
Using Eq. (4), the mean parameter
Thus,
The ``inverse" regression, of
Thus, binv is biased relative to
In the case of linear, stochastic biasing,
the above parameters reduce to
Thus, b1
In the fully degenerate case of linear and deterministic biasing,
all the b parameters are the same, and only then r = 1.
In actual applications,
the above local biasing parameters are involved when the parameter
``
Another useful way of estimate 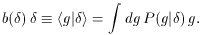
 .
The function b(
.
The function b( ) allows
for any possible non-linear biasing.
We find it useful to characterize the function b(
) allows
for any possible non-linear biasing.
We find it useful to characterize the function b( )
by its moments
)
by its moments  and
and
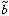 defined by
defined by
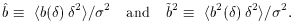
 is the
natural extension of b1
and that
is the
natural extension of b1
and that 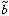 /
/
 is the relevant measure of
non-linearity, independent of stochasticity.
is the relevant measure of
non-linearity, independent of stochasticity.
 Define the random biasing field
Define the random biasing field  by
by

 g - < g |
g - < g |  >, with <
>, with <  |
|  > = 0.
The local variance of
> = 0.
The local variance of  at a
given
at a
given  defines the biasing
scatter
function
defines the biasing
scatter
function  b(
b( ) and by averaging over
) and by averaging over  one obtains the local biasing scatter parameter:
one obtains the local biasing scatter parameter:
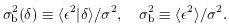
 2 is
for convenience.
The function <
2 is
for convenience.
The function <  2
|
2
|  >1/2 is marked by
error bars in
Figure 1.
Here and below we make use of a straightforward lemma,
valid for any functions p(g) and q
(
>1/2 is marked by
error bars in
Figure 1.
Here and below we make use of a straightforward lemma,
valid for any functions p(g) and q
( ):
):
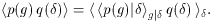
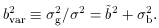

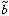 .
This makes bvar biased compared to
.
This makes bvar biased compared to
 ,
,
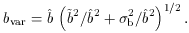
 is related to the covariance,
is related to the covariance,
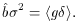
 is the slope of the linear regression of g on
is the slope of the linear regression of g on
 ,
which makes it a natural generalization of b1.
Unlike the variance
,
which makes it a natural generalization of b1.
Unlike the variance  g2 in Eq. (5), the covariance in Eq. (7)
has no contribution from
g2 in Eq. (5), the covariance in Eq. (7)
has no contribution from  b.
A complementary parameter to bvar is the linear
correlation coefficient,
b.
A complementary parameter to bvar is the linear
correlation coefficient,
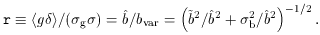
 on g, yields another biasing parameter:
on g, yields another biasing parameter:
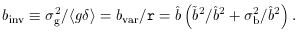
 , even more than
bvar.
The parameter binv is close to what is measured in practice
by two-dimensional linear regression
[52],
because the errors in
, even more than
bvar.
The parameter binv is close to what is measured in practice
by two-dimensional linear regression
[52],
because the errors in  are
larger than in g.
Note that
are
larger than in g.
Note that 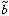 and
and
 b nicely separate the
non-linearity and stochasticity, while bvar, r
and binv mix them.
b nicely separate the
non-linearity and stochasticity, while bvar, r
and binv mix them.
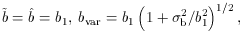
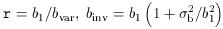
 bvar
bvar  binv.
In the case of non-linear deterministic biasing:
binv.
In the case of non-linear deterministic biasing:
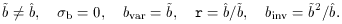
 ''
is measured from observational data.
For linear and deterministic biasing this parameter is defined unambiguously
as
''
is measured from observational data.
For linear and deterministic biasing this parameter is defined unambiguously
as  1
1
 f
(
f
( ) /
b1, but any deviation from this
model causes us to measure different
) /
b1, but any deviation from this
model causes us to measure different
 's by the
different methods. For example,
it is
's by the
different methods. For example,
it is  var
var
 f (
f ( ) / bvar which is
determined from
) / bvar which is
determined from  g
and
g
and  f (
f ( ).
The former is typically determined from a redshift survey,
and the latter either from an analysis of peculiar velocity data,
from the abundance of rich clusters,
or by COBE normalization of a specific power-spectrum shape.
In the case of stochastic biasing bvar
is always an overestimate of
).
The former is typically determined from a redshift survey,
and the latter either from an analysis of peculiar velocity data,
from the abundance of rich clusters,
or by COBE normalization of a specific power-spectrum shape.
In the case of stochastic biasing bvar
is always an overestimate of 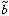 ,
Eq. (5), and when the biasing is linear
bvar is an overestimate of
b1. Therefore
,
Eq. (5), and when the biasing is linear
bvar is an overestimate of
b1. Therefore  var is underestimated
accordingly.
var is underestimated
accordingly.
 is via the linear regression of the fields in our cosmological
neighborhood, e.g., -
is via the linear regression of the fields in our cosmological
neighborhood, e.g., - .
v(x) on g (x)
[17,
33,
52].
In the mildly-non-linear regime, -
.
v(x) on g (x)
[17,
33,
52].
In the mildly-non-linear regime, - . v(x) is actually replaced by
another function of the first spatial
derivatives of the velocity field, which better approximates the
scaled mass-density field f (
. v(x) is actually replaced by
another function of the first spatial
derivatives of the velocity field, which better approximates the
scaled mass-density field f ( )
) (x)
[47].
The regression is effectively
(x)
[47].
The regression is effectively  on g, because the errors in
on g, because the errors in
 . v (or f
. v (or f
 ) are
typically more than twice as large as the errors in g.
Hence, the measured parameter is close to
) are
typically more than twice as large as the errors in g.
Hence, the measured parameter is close to
 inv
inv
 f
(
f
( ) / binv.
In the case of linear and stochastic biasing, Eq. (10), binv
is an overestimate of b1 so
the corresponding
) / binv.
In the case of linear and stochastic biasing, Eq. (10), binv
is an overestimate of b1 so
the corresponding  is underestimated accordingly.
is underestimated accordingly.