


For the analysis of redshift-distortion we need to
deal with spatial correlations.
Given the random biasing field  ,
we define the two-point biasing-matter cross-correlation function
and the biasing auto-correlation function by
,
we define the two-point biasing-matter cross-correlation function
and the biasing auto-correlation function by
where the averaging is over the ensembles at points 1 and 2 separated by
r. We define the biasing as local if
Note that the biasing parameter that appears here is
b1, not bvar.
To see how the power spectra are affected by the biasing scatter,
we approximate the local biasing by a step function:
where Vb is the volume associated with rb.
We see that the local biasing scatter adds a constant to
Pgg(k).
We can now proceed to estimating
Recalling that the power spectra are the Fourier transforms of the
corresponding correlation functions, one can equivalently write an
expression involving Pggs(k),
Pgg(k), Pgm(k) and
Pmm(k),
or the analogous spherical harmonics.
Next we tie in the biasing scheme.
In the simplified case of linear and deterministic biasing, one simply has
Pgg = b1Pgm =
b12Pmm, so the distortion
relation reduces to Kaiser's
formula [36],
Pggs =
Pgg(1 + µ2
In the more realistic case of linear, local, and stochastic
biasing, first at zero lag,
In this local equation both bvar and r are
involved in a
non-trivial way; the distortions depend on the scatter, reflecting
the
This is simply the Kaiser formula again, which, unlike Eq. (16), is
independent of the biasing scatter!
It involves only the mean biasing parameter b1, in an
expression that is indistinguishable from the deterministic case.
This is a straightforward result of the assumed locality of the biasing scheme:
the biasing scatter at two distant points is uncorrelated and therefore its
contribution to
The distortion relation for P(k) becomes more complicated because
of the additive term in Eq. (14). For linear biasing, when substituting
Eq. (14) in the linear distortion relation, the terms analogous to the ones
involving b1-1 and
b1-2 in Eq. (17) for
Equation (7) of Pen [50],
which involves bvar and r like our
Eq. (16), may leave the impression that the redshift-distortion
expression depends on the scatter. In order to obtain his relation
from the general distortion relation, one has to define
k-dependent biasing parameters by Pgg(k) =
bvar(k)2Pmm(k)
and Pgm(k) =
bvar(k)r(k)
Pmm(k).
(Pen's
While its sensitivity to stochasticity is indirect,
the redshift distortion analysis is sensitive to
the non-linearity, of the biasing. A proper analysis
would require a non-linear treatment including
a non-linear generalization of the GI relation
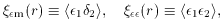
 em(r)
= 0 for any r and
em(r)
= 0 for any r and


 (r) = 0 for r > rb,
where rb is on the order of the basic smoothing scale.
Using lemmas that are two-point equivalents of Eq. (4),
one obtains analogous relations to Eqs. (7) and (5).
In the case of linear and local biasing, these become
(r) = 0 for r > rb,
where rb is on the order of the basic smoothing scale.
Using lemmas that are two-point equivalents of Eq. (4),
one obtains analogous relations to Eqs. (7) and (5).
In the case of linear and local biasing, these become
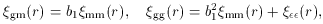


 (r) =
(r) =
 b2
b2
 2 for r <
rb and zero otherwise.
Recalling that the power spectra are the Fourier transforms of
the corresponding correlation functions,
we get for k << rb-1, from Eq. (13),
2 for r <
rb and zero otherwise.
Recalling that the power spectra are the Fourier transforms of
the corresponding correlation functions,
we get for k << rb-1, from Eq. (13),
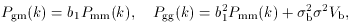
 via redshift distortions
[36,
28,
29,
30,
25,
31,
11,
24,
40].
To first order, the local galaxy density fluctuations in redshift space
(gs) and real space (g) are related by
gs = g - ðu / ðr,
where u is the radial component of the peculiar velocity v.
Assuming no velocity biasing, linear GI predicts
ðu / ðr = - µ2
f(
via redshift distortions
[36,
28,
29,
30,
25,
31,
11,
24,
40].
To first order, the local galaxy density fluctuations in redshift space
(gs) and real space (g) are related by
gs = g - ðu / ðr,
where u is the radial component of the peculiar velocity v.
Assuming no velocity biasing, linear GI predicts
ðu / ðr = - µ2
f( )
)
 ,
where µ2 is a geometrical
factor depending on the angle between v and x.
Thus, the basic linear relation for redshift distortions is
gs = g +
fµ2
,
where µ2 is a geometrical
factor depending on the angle between v and x.
Thus, the basic linear relation for redshift distortions is
gs = g +
fµ2 .
The general expression for redshift distortions
is obtained from this basic relation by averaging
< g1s g2s >
over the distributions of
.
The general expression for redshift distortions
is obtained from this basic relation by averaging
< g1s g2s >
over the distributions of
 at a pair of
points separated by r:
at a pair of
points separated by r:
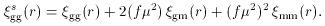
 1)2,
where
1)2,
where  1
1
 f(
f( ) / b1.
) / b1.


 (0) =
(0) =
 b2
b2
 2 and
2 and
 gg(0) =
bvar2
gg(0) =
bvar2  mm(0). Then, via Eq. (5) and Eq. (7), the general
distortion relation, Eq. (15), reduces to
mm(0). Then, via Eq. (5) and Eq. (7), the general
distortion relation, Eq. (15), reduces to
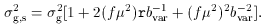
 b2
term in Eq. (5).
On the other hand, at large separations r > rb,
where
b2
term in Eq. (5).
On the other hand, at large separations r > rb,
where 

 vanishes,
one obtains instead, from Eq. (13),
vanishes,
one obtains instead, from Eq. (13),
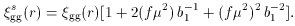
 gg cancels out.
gg cancels out.
 are multiplied by [1 -
are multiplied by [1 -
 b2
b2
 2 Vb /
Pgg(k)], a function of k.
The distortion relation for P(k) is thus affected by the biasing
scatter in a complicated way.
However, there may be a significant k range around the peak
of P(k) in which the additive scatter term is small compared
to the rest. In this range the relation reduces to an expression
similar to Eq. (17) for the corresponding power spectra.
Still, the scatter term always dominates Eq. (14) at small
and at large k's.
2 Vb /
Pgg(k)], a function of k.
The distortion relation for P(k) is thus affected by the biasing
scatter in a complicated way.
However, there may be a significant k range around the peak
of P(k) in which the additive scatter term is small compared
to the rest. In this range the relation reduces to an expression
similar to Eq. (17) for the corresponding power spectra.
Still, the scatter term always dominates Eq. (14) at small
and at large k's.
 refers to
his b1, which is
our bvar, except that he allows it to vary with k).
In the case of local biasing, a comparison to our Eq. (14)
yields bvar(k)2 =
b12 +
refers to
his b1, which is
our bvar, except that he allows it to vary with k).
In the case of local biasing, a comparison to our Eq. (14)
yields bvar(k)2 =
b12 +
 b2
b2
 2Vb / Pmm(k)
and bvar(k) r(k) =
b1.
In the k range near the peak of Pmm(k),
where the constant term
in Eq. (14) may be negligible, one has bvar(k)
= b1 and r(k) = 1,
and there is indeed no sign of the stochasticity in the distortion relation.
2Vb / Pmm(k)
and bvar(k) r(k) =
b1.
In the k range near the peak of Pmm(k),
where the constant term
in Eq. (14) may be negligible, one has bvar(k)
= b1 and r(k) = 1,
and there is indeed no sign of the stochasticity in the distortion relation.
 . v =
-f
. v =
-f ,
because the non-linear effects of biasing and gravity enter at the same
order.
The result is more complicated than Eq. (15), but is calculable
in principle once one knows the function
b(
,
because the non-linear effects of biasing and gravity enter at the same
order.
The result is more complicated than Eq. (15), but is calculable
in principle once one knows the function
b( ) and the one-
and two-point probability distribution functions of
) and the one-
and two-point probability distribution functions of
 .
.