The key feature in our biasing formalism is the natural separation
between non-linear and stochastic effects. The non-linearity is
expressed by the conditional mean via
b(
), and the
statistical scatter is measured by the
conditional standard deviation,
b(), and higher moments if necessary.
For analyses using local moments of second order,
the biasing scheme is characterized by three parameters:
measuring the mean biasing,
/
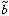measuring the effect of non-linearity,
and b/ measuring the effect of stochasticity.
Deviations from linear and deterministic biasing typically
result in biased estimates of
,
which depend on the actual method of measurement.
The non-linearity and the scatter lead to underestimates of order
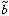2 /
2 and
b2 /
2 respectively in the
different
estimators of
relative to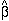 
=
f(
) /
.
Based on N-body simulations and toy models,
the effects of non-linear biasing are typically on the order of 20%
or less, and the effects of scatter could be larger.
One expects the
parameters
to be biased in the following order:
inv <
var <
.
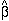The stochasticity affects the linear redshift-distortion analysis only by
limiting the useful range of scales.
In this range, the basic expression reduces to the simple
Kaiser formula for b() =
= b1 (not
bvar), and it does not involve the scatter at all.
The distortion analysis is in principle sensitive to the
non-linear properties of biasing, but they
are expected to be weak, and of the same order as
the effects of non-linear GI.
This is good news for the prospects of measuring an unbiased
from redshift distortions in the large redshift surveys of the near
future (2dF and SDSS).
The study of stochastic and non-linear biasing should be extended to address the time evolution of biasing because many relevant measurements of galaxy clustering are now being done at high redshifts. As seen in Fig. 1, the biasing is clearly a strong function of cosmological epoch [21, 26, 46, 56, 55, 2, 45, 59, 58, 48]. In particular, if galaxy formation is limited to a given epoch and the biasing is linear, one can show [26] that the linear biasing factor b1 would eventually approach unity as a simple result of the continuity equation. Tegmark & Peebles [58] have recently generalized the analytic study of time evolution to the case of stochastic but still linear biasing and showed how bvar and r approach unity in this case. These studies should be extended to the general non-linear case using our formalism. Our current simulations [54] are aimed at this goal. The analysis of simulations could also be extended to include non-local biasing, using the biasing correlations as defined here.
The PDF (or count in cells) of galaxy density from a large-scale redshift
survey, plus an estimate of of
the corresponding mass density, allow a measure of the mean biasing
function b() and the
corresponding non-linearity parameter
/
.
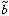This can be done at low or high redshifts.
Mapping of the biasing field in our cosmological neighborhood,
and estimates of the biasing scatter, are feasible with current
and future measurements of peculiar velocities
and careful comparisons to the galaxy distribution.
The reconstruction of the large-scale mass distribution
based on weak gravitational lensing
is also becoming promising for this purpose.
In summary,
in order to use the measurements of
for an accurate
evaluation
of , one should consider the
effects of non-linear and stochastic
biasing and the associated complications of scale dependence, time
dependence, and type dependence.
The current different estimates are expected to span a range of
~ 30% in due to
stochastic and non-linear biasing.
The analysis of redshift distortions seems to be most promising;
once it is limited to the appropriate range of scales, the analysis is
independent of stochasticity and the non-linear effects are expected to be
relatively small. The mean biasing function can be extracted from
the galaxy PDF, and the scatter from theory and local cosmography.
Acknowledgements I thank O. Lahav, G. Lemson, A. Nusser, M.J. Rees, Y. Sigad, R. Somerville, M.A. Strauss, D.H. Weinberg and S.D.M. White for collaboration and stimulating discussions. This research was supported in part by the US-Israel Binational Science Foundation grant 95-00330, and by the Israel Science Foundation grant 950/95.