In the Big Bang model, the age of the universe, t0,
is a function of three parameters: h, 
m and 
(1).
The dimensionless Hubble constant, h,
tells us how fast the universe is expanding.
The density of matter in the universe, m, slows the expansion, and the cosmological
constant, , speeds up the expansion
(Fig. 1).
|
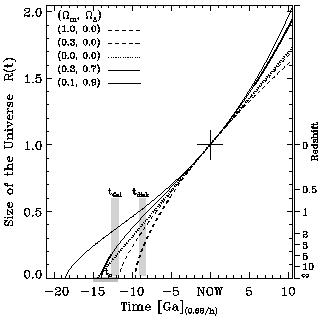
Figure 1. The size of the universe, in
units of its current size, as a function of time.
The age of the five models can be read from the x axis
as the time between NOW and the intersection of the
model with the x axis.
The main result of this paper, t0 = 13.4 ± 1.6
Ga, is labeled
``t0'' and is shaded gray on the x axis.
Measurements of the age of the halo of our Galaxy yield
tGal = 12.2
± 0.5 Ga, whereas measurements of the age of the disk of our
Galaxy yield tdisk = 8.7 ± 0.4 Ga
(Table 2). These age ranges are also
labeled and shaded gray.
The ( |
Until recently, large uncertainties in the measurements of h,
m and made efforts to determine
t0(h, m, ) unreliable.
Theoretical preferences were, and still are, often used to remedy these
observational uncertainties. One assumed the standard model (m = 1, = 0),
dating the age of the universe to t0 = 6.52 / h
billion years old (Ga).
However, for large or even moderate h estimates
(
0.65),
these simplifying assumptions resulted in an age crisis in which the universe
was younger than our Galaxy (t0
10 Ga < tGal
12 Ga).
These assumptions also resulted in a baryon crisis in which estimates of the
amount of normal (baryonic) matter in the universe were in conflict
(2,
3).
Evidence in favor of m < 1 has become more compelling
(4,
5,
6,
7,
8),
but is still
often assumed to be zero, not because it is measured to be so,
but because models are simpler without it.
Recent evidence from supernovae (SNe)
(4,
5)
indicates that > 0.
These SNe data and other data exclude the standard Einstein-deSitter
model (m = 1, = 0).
The cosmic microwave background (CMB), on the other hand, excludes
models with low m
and = 0
(3). With both
high and low
m excluded, cannot be zero.
Combining CMB measurements with SNe and other data,
I (9)
have reported =
0.62 ± 0.16.
[see (10,
11,
12) for similar
results]. If 
0, then estimates of the age of the universe in Big Bang
models must
include . Thus one must use the most
general form: t0 =
f (m, ) / h,
(13).
|
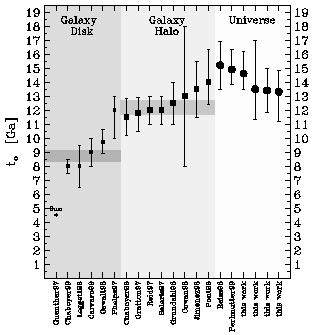
Figure 2. Age estimates of the universe and
of the oldest objects in our Galaxy.
The four estimates of the age of the universe from this work are indicated
in Table 2.
The three similar points near 13.4 Ga, result from h = 0.64, 0.68, 0.72
and indicate that the result is not strongly dependent on h when
a reasonable h uncertainty of ± 0.10 is used.
Among the four, the highest value at 14.6 Ga comes from assuming h =
0.64 ± 0.02. All the estimates in the top section of
Table 2 are plotted here.
As in Fig. 1, averages of the ages of the
Galactic halo and Galactic disk are shaded gray.
The absence of any single age estimate more than ~ 2 |
Here I have combined recent independent measurements of CMB anisotropies (9), type Ia SNe (4, 5), cluster mass-to-light ratios (6), cluster abundance evolution (7), cluster baryonic fractions (14), deuterium-to-hydrogen ratios in quasar spectra (15), double-lobed radio sources (8), and the Hubble constant (16) to determine the age of the universe. The big picture from the analysis done here is as follows (Figs. 1 and 2): The Big Bang occurred at ~ 13.4 Ga. About 1.2 billion years (Gy) later, the halo of our Galaxy (and presumably the halo of other galaxies) formed. About 3.5 Gy later, the disk of our Galaxy (and presumably the disks of other spiral galaxies) formed. This picture agrees with what we know about galaxy formation. Even the recent indications of the existence of old galaxies at high redshift (17) fit into the time framework determined here. In this sense, the result is not surprising. What is new is the support given to such a young age by such a wide array of recent independent measurements.
> 0).
This acceleration means we are in a period of slow inflation.
Other consequences of a 
from the average
adds plausibility to the possibly overdemocratic
procedure of computing the variance-weighted averages.
The result that t0 > tGal is
logically inevitable, but the standard
Einstein-deSitter model does not satisfy this requirement unless
h < 0.55.
The reference for each measurement is given under the x axis.
The age of the sun is accurately known and is included for reference.
Error bars indicate the reported 1