


At large distances from the galactic centre the gravitational
potential should be that produced by a central point mass and, in
the absence of forces other than gravitation, it should be expected
that
GM/R2 = ![]() /R (G, universal gravitation constant; M,
galactic mass; R, galactocentric radius;
/R (G, universal gravitation constant; M,
galactic mass; R, galactocentric radius; ![]() , rotation
velocity), therefore
, rotation
velocity), therefore
![]()
![]() R-1/2, which is called, for
obvious reasons, the Keplerian rotation curve. This Keplerian decline was
not observed, but rather, flat rotation curves with
R-1/2, which is called, for
obvious reasons, the Keplerian rotation curve. This Keplerian decline was
not observed, but rather, flat rotation curves with ![]() =cte were
obtained. Apparently, this has the direct implication that
M
=cte were
obtained. Apparently, this has the direct implication that
M ![]() R,
thus depending on the quality of the telescope used. The "Dark
Matter" (DM) hypothesis interprets this result in the sense that the
Keplerian regime holds at much greater distances than those
at which we obtain observations. There should be great quantities of
dark matter
extending far beyond the visible matter in a more or less spherically
symmetric DM halo. If its distribution is spherically symmetric, the
mass interior to a sphere of radius R would be
M(R)
R,
thus depending on the quality of the telescope used. The "Dark
Matter" (DM) hypothesis interprets this result in the sense that the
Keplerian regime holds at much greater distances than those
at which we obtain observations. There should be great quantities of
dark matter
extending far beyond the visible matter in a more or less spherically
symmetric DM halo. If its distribution is spherically symmetric, the
mass interior to a sphere of radius R would be
M(R) ![]() R, so
that we obtain a first rough model of DM density distribution:
R, so
that we obtain a first rough model of DM density distribution:
![]() = (1/4
= (1/4![]() R2)dM/dR =
R2)dM/dR = ![]() /4
/4![]() GR2, i.e.
GR2, i.e.
![]()
![]() R-2, for distances far beyond the
visible radius. This model is
obviously over simplified, as we will see, but it coincides with
the so called "nonsingular isothermal" profile
R-2, for distances far beyond the
visible radius. This model is
obviously over simplified, as we will see, but it coincides with
the so called "nonsingular isothermal" profile
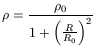
| (1) |
(with ![]() and R0 being constants), one of
the most frequently types of halos.
and R0 being constants), one of
the most frequently types of halos.
The interpretation of rotation curves of spiral galaxies as evidence
of DM halos was probably first proposed by
Freeman (1970)
who noticed that the expected Keplerian decline was not present
in NGC 300 and M33, and considered an undetected mass,
with a
different distribution for the visible mass. The observation of flat
rotation curves was later confirmed and the DM hypothesis reinforced
by successive studies.
Rubin, Ford and Thonnard
(1980)
and Bosma
(1978,
1981a,
b)
carried out an extensive study, after which the existence of DM
in spiral galaxies was widely accepted.
Van Albada et al. (1985)
analyzed the rotation of NGC 3198 and the distribution of its
hypothetical DM, concluding that this galaxy has a dark halo, in
agreement with the paper by
Ostriker and Peebles (1987)
about the
stability of disks. The rotation of spirals was soon considered the most
solid proof for the existence of DM in the Universe, particularly
important when it was later believed that ![]() = 1. Other decisive
papers were produced by
Begeman (1987) and
Broeils (1992).
= 1. Other decisive
papers were produced by
Begeman (1987) and
Broeils (1992).
The initial conclusion could be schematized by considering the rotation curve to be high and flat. If it is high, the dark halo should be very massive; if it is flat, the dark halo should be very large. Indeed, the flatness of the rotation curves was explained "too" well, because if the disk and halo had such different distributions, very careful matching was required between the falling disk rotation curve and the rising halo one. The curve was "too" flat; there was a "disk-halo conspiracy" (Bahcall and Casertano, 1985, van Albada and Sancisi, 1986).
The only explanation offered for this "conspiracy" is the adiabatic compression of the halo material when the disk was formed (Barnes 1987, Blumenthal et al. 1986) (which is commented later) although Bosma (1998) gave a list of galaxies for which this mechanism is not fully operational. The disk-halo conspiracy is a problem that remains to be satisfactorily solved. The problem is not why curves are flat (not all are flat) but why the transition from disk to halo domination is so smooth.
Different procedures have been used to obtain dark matter
distribution: stellar distribution is determined from photometric
observations and must then be complemented with CO and HI observations
(with a correction factor to include the He mass) mainly for late spirals,
in order to assess the gas profiles. These data determine the densities of
bulge, disk and gas in the disk, or rather their contribution to the
rotation velocity through the so called "circular velocity",
Vc(R), which would coincide with the true
rotation velocity
![]() , if the component were dominant in the galaxy. The rotation
curve,
, if the component were dominant in the galaxy. The rotation
curve, ![]() (R), is determined mainly with 21 cm maps. The addition
of the different visible components does not, in general, coincide
with
(R), is determined mainly with 21 cm maps. The addition
of the different visible components does not, in general, coincide
with ![]() (R), from which the existence of a DM halo is deduced.
(R), from which the existence of a DM halo is deduced.
Then, to obtain its distribution, there are several different techniques. One of the most widely used is the "maximum disk hypothesis" (see for instance, Begeman, Broeils and Sanders, 1991). Here, the mass to light, M/L, ratio is fixed for the different visible components, with values higher than about 10 being difficult to assign to a stellar population. Then, the innermost regions are adjusted so that the disk is able to produce the observed rotation curve without a halo. The disk M/L obtained is then kept constant at all radii and the circular velocity of the halo is then obtained for higher radii. Another possibility is the so called "best fit" technique. In this case, it is necessary to adopt a halo profile defined with several adjustable parameters. Most decompositions have adopted the isothermal spherical profile. At present, it might be profitable to investigate the alternative NFW profile, as this has a higher theoretical justification (we will come back to this point in the section devoted to theoretical models). The problem with the best fit procedure is that the halo distribution function must be known although, in part, this is precisely what we want to obtain.
The maximum disk technique was introduced by van Albada and Sancisi (1986). There are some psychological aspects to their introduction: "dark matter is a daring assumption; the intention is therefore to make the halo as small as possible, at least in the traditional optical best known innermost regions and reserve the exotic physics for the outer radio observable regions. It can therefore be found as noticeable that "maximum disk" fits are reasonable and do not very much differ from other fits. This gives us a first information: the inner parts do not require large amounts of dark matter". This conclusion was "a priori" not obvious. At present, it is considered that the amounts of dark and visible matter in the optical disks are similar, with not so much DM being needed as in the outermost disks.
The basic initial description consisting of an innermost region in
which ![]() (R) increased linearly followed by a constant
(R) increased linearly followed by a constant
![]() in the outer region was soon considered too simple.
Casertano and van Gorkom (1991)
found galaxies with declining rotation curves
and analyzed current observations to show that bright compact galaxies
have slightly declining rotation curves and that rising curves are
predominant in low-luminosity galaxies (see also
Broeils, 1992).
This latter fact indicated that low-luminosity galaxies are more DM rich
and that, in general, there is an increase in the dark matter fraction
with decreasing luminosity
(Persic and Salucci, 1988,
1990).
Nearly all rotation curves belonging to
the different types of spirals can be described by means of a
single function, the so called "Universal Rotation Curve"
(Persic, Salucci and Stel,
1996;
Salucci and Persic, 1997)
which is a successful fit of galactic astronomy that will be commented
later.
in the outer region was soon considered too simple.
Casertano and van Gorkom (1991)
found galaxies with declining rotation curves
and analyzed current observations to show that bright compact galaxies
have slightly declining rotation curves and that rising curves are
predominant in low-luminosity galaxies (see also
Broeils, 1992).
This latter fact indicated that low-luminosity galaxies are more DM rich
and that, in general, there is an increase in the dark matter fraction
with decreasing luminosity
(Persic and Salucci, 1988,
1990).
Nearly all rotation curves belonging to
the different types of spirals can be described by means of a
single function, the so called "Universal Rotation Curve"
(Persic, Salucci and Stel,
1996;
Salucci and Persic, 1997)
which is a successful fit of galactic astronomy that will be commented
later.


