


13.1. Evolution of the comoving luminosity density and SFR
As illustrated in Fig. 3, the CIRB intensity and spectral distribution are in clear support of models for evolving starbursts discussed above.
Unfortunately, we are not yet in the position to derive an independent assessment of the evolutionary SFR density based on the available complete samples of faint IR sources: although a substantial effort to follow them up in the optical has started (particularly good chances are offered by ongoing spectroscopic follow-up of the statistically rich faint ISOCAM samples like the GITES and HDFs), the process is far from complete. As a consequence, no detailed conclusions can yet be drawn about the contribution of IR sources to the global comoving luminosity and SFR densities (Madau et al. 1996).
Only rather model-dependent estimates are possible at the moment, based
for example on the evolution scheme described in
Sect. 11 and whose predictions
are summarized in Figure 14.
There is a clear indication here that the contribution of
IR-selected sources to the luminosity density at high-z
should significantly exceed those based on optically selected sources,
and that the excess may be progressive with redshift up to z ![]() 1.
1.

|
Figure 14. Evolution of the metal
production rates (left axis) and of the star formation rates
(right axis) based on the modelisation of IR counts and z-distributions
in Sect 11.1 (case
|
This evolution should however level off at higher z, to allow consistency with the observed z-distributions for faint ISOCAM sources (Franceschini et al. 2000) and with the estimates of the average time-dependent emissivity jeff(z) (eq. [8.21]) based on deconvolution of the CIRB spectrum (Gispert et al. 2000).
Altogether these results indicate that the history of galaxy
long-wavelength emission
does probably follow a path similar to that revealed by optical-UV
observations, by showing a similar peak activity around z ![]() 1, rather than being
confined to the very high-z, as sometimes was suggested.
This confirms that the bulk of the galaxy activity, and particularly the
bulk of the energy released in the CIRB background, is to
be placed around z = 1, which is obvious from
Fig. 14 if the dependence of the
cosmological timescale on redshift is considered
(Harwit 1999;
Haarsma & Partridge
1998).
1, rather than being
confined to the very high-z, as sometimes was suggested.
This confirms that the bulk of the galaxy activity, and particularly the
bulk of the energy released in the CIRB background, is to
be placed around z = 1, which is obvious from
Fig. 14 if the dependence of the
cosmological timescale on redshift is considered
(Harwit 1999;
Haarsma & Partridge
1998).
These results can only be preliminary untill we will have more substantial identifications of existing IR-selected source samples, or, better, after the fleet of IR/mm facilities planned for this and the next decade will have eventually provided data of enough quality to allow a full long-wavelength complement to the optical-UV high-z observations.
13.2. Energy constraints from background observations
In the present situation, the most robust constraints on the high-redshift far-IR/sub-mm population come from observations of the global energetics residing in the CIRB and optical background radiations. The latter imply a very substantal demand on contributing sources, as detailed below in schematic terms.
Let us assume that a fraction f * of the universal mass density in baryons
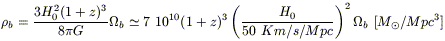
| (13.29) |
undergoes a transformation (either processed in stars or by
gravitational fields) with radiative efficiency ![]() , then the locally observed energy density
of the remnant photons is
, then the locally observed energy density
of the remnant photons is
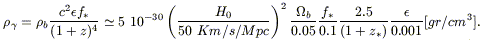
| (13.30) |
For stellar processes, ![]() is
essentially determined, within the moderate uncertainties of stellar models,
by the IMF:
is
essentially determined, within the moderate uncertainties of stellar models,
by the IMF:
![]() = 0.001 for a Salpeter IMF and a low-mass cutoff
Mmin = 0.1 M
= 0.001 for a Salpeter IMF and a low-mass cutoff
Mmin = 0.1 M![]() (see eq. 4.13),
(see eq. 4.13),
![]() = 0.002 and
= 0.002 and
![]() = 0.003
for Mmin = 2 and Mmin = 3, while
= 0.003
for Mmin = 2 and Mmin = 3, while ![]() gets the usually quoted value of
gets the usually quoted value of
![]() = 0.007 only for
Mmin > 10 M
= 0.007 only for
Mmin > 10 M![]() [A. Bressan, private communication].
[A. Bressan, private communication].
Note how the contribution to the photon background energy by very high redshifts is penalized in eq. (13.30) by the (1 + z)-1 factor: measurements of the photon background preferentially constrain source emission at moderate z, whereas estimates of the local average metal abundance (obviously much more difficult and indirect!) would in principle provide a less biased integral over the total stellar yield in the past.
13.2.1. Constraints from the integrated optical background
As already noticed (Sect. 8.3.1), the
converging galaxy counts at faint magnitudes observed in the optical
and near-IR allow to estimate with fair accuracy the total diffuse flux
at these wavelengths (Fig. 3, see
Madau & Pozzetti 2000).
The bolometric emission from 0.1 to 7 ![]() m by distant galaxies turns out to be
m by distant galaxies turns out to be
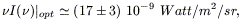
| (13.31) |
which in fact is a lower limit if we give credit to claims of a (× 2 - 3) larger optical/NIR background, see Sect. 8.1 (but see also a counter-argument in Sect. 8.2).
We discussed evidence that for the most luminous starbursts the optical
spectra are only moderately contributed by starburst emission, which is
mostly hidden in the far-IR. Accordingly, let us assume
that the optical/NIR BKG mostly originates by quiescent SF in spiral
disks and by intermediate and low-mass stars. As observed in the Solar
Neighborhood, a good
approximation to the IMF in such relatively quiescent environments is the
Salpeter law with standard low-mass cutoff, corresponding to a mass-energy
conversion efficiency
![]()
![]() 0.001. With these parameter values, we
can reproduce the whole optical BKG intensity of eq. (13.31) by
transforming a fraction
f *
0.001. With these parameter values, we
can reproduce the whole optical BKG intensity of eq. (13.31) by
transforming a fraction
f * ![]() 10% of all nucleosynthetic baryons into
low-mass stars, assumed the bulk of this process happened at
z *
10% of all nucleosynthetic baryons into
low-mass stars, assumed the bulk of this process happened at
z * ![]() 1.5
and 5% of the closure value in baryons (for our adopted
H0 = 50 Km/s/Mpc, or
1.5
and 5% of the closure value in baryons (for our adopted
H0 = 50 Km/s/Mpc, or
![]() h2 = 0.012, consistent with
the theory of primordial nucleosynthesis):
h2 = 0.012, consistent with
the theory of primordial nucleosynthesis):
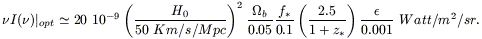
|
It is generated in this way a local density in low-mass stars consistent with the observations (based on photometric surveys, Ellis et al. 1996, and assuming standard mass to light ratios):
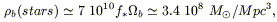
| (13.32) |
which, assuming typical solar metallicities, corresponds to a local density in metals of
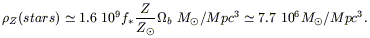
| (13.33) |
Note that a factor 2-3 larger optical/NIR background than in eq. (13.31) could still be consistent with the present scheme if a similar scaling factor would also apply to eqs. (13.32) and (13.33): that is, if both the excess background and low-mass stars and stellar metals would be due to extended low-brightness halos, unaccounted for by deep HST imaging as well as by local photometric surveys.
13.2.2. Explaining the CIRB background
The total energy density between 7 and 1000 ![]() m contained in the CIRB,
including modellistic extrapolations as in
Fig. 3 consistent with the constraints set
by the cosmic opacity observations, amounts to
m contained in the CIRB,
including modellistic extrapolations as in
Fig. 3 consistent with the constraints set
by the cosmic opacity observations, amounts to
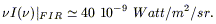
| (13.34) |
Following our previous assumption that luminous starbursting galaxies
emit negligible energy in the optical-UV and most of it in the far-IR,
we coherently assume that the energy resident in the CIRB background
originates from star-forming galaxies at median
z * ![]() 1.5. The amount of baryons
processed in this phase and the conversion efficiency
1.5. The amount of baryons
processed in this phase and the conversion efficiency ![]() have to account for the combined constraint set by eqs. (13.32) and
(13.34), that is to provide a huge amount of energy with essentially
no much stellar remnant in the local populations. The only plausible
solution
is then to change the assumptions about the stellar IMF characterizing
the starburst phase, for example to a Salpeter distribution cutoff below
Mmin = 2 M
have to account for the combined constraint set by eqs. (13.32) and
(13.34), that is to provide a huge amount of energy with essentially
no much stellar remnant in the local populations. The only plausible
solution
is then to change the assumptions about the stellar IMF characterizing
the starburst phase, for example to a Salpeter distribution cutoff below
Mmin = 2 M![]() , with a correspondingly higher
efficiency
, with a correspondingly higher
efficiency ![]() = 0.002
(see discussion in Sect. 13.2). This may explain the
energy density in the CIRB:
= 0.002
(see discussion in Sect. 13.2). This may explain the
energy density in the CIRB:
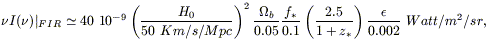
|
assumed that a similar amount of baryons,
f * ![]() 10%, as processed with low
efficiency during the "inactive" secular evolution, are processed with
higher efficiency during the starbursting phases, producing a two times
larger amount of metals:
10%, as processed with low
efficiency during the "inactive" secular evolution, are processed with
higher efficiency during the starbursting phases, producing a two times
larger amount of metals:
![]() (metals)
(metals) ![]() 1.4 107 M
1.4 107 M![]() /Mpc3.
Note that by decreasing Mmin during the SB phase would
decrease the efficiency
/Mpc3.
Note that by decreasing Mmin during the SB phase would
decrease the efficiency
![]() and increase
the amount of processed baryons f * , hence
would bring to exceed the locally
observed mass in stellar remnants (eq. [13.32]).
and increase
the amount of processed baryons f * , hence
would bring to exceed the locally
observed mass in stellar remnants (eq. [13.32]).
The above scheme is made intentionally extreme, to illustrate the point. The reality is obviously more complex than this, e.g. by including a flattening at low mass values in the Salpeter law (see Zoccali et al 2000) for the solar-neighborhood SF and, likewise, a more gentle convergence of the starburst IMF than a simple low-mass cutoff.
13.2.3. Galactic winds and metal pollution of the inter-cluster medium
A direct prediction of our scheme above is that most of the metals produced during the starburst phase have to be removed by the galaxies to avoid largely exceeding the locally observed metals in galaxies. As discussed in Sect. 6.4, there is clear evidence in local starbursts, based on optical and X-ray observations, for large-scale super-winds out-gassing high-temperature enriched plasmas from the galaxy. Our expectation would be that a substantial amount of metals, those originating from the same SF processes producing the CIRB background, are hidden in the hot inter-cluster medium.
But where all these metals are?
While densities and temperatures of the polluted plasmas in the diffuse (mostly primordial and un-processed) inter-cluster medium are such to hide easily these products of the ancient SB phase, an interesting support to the above scheme comes from consideration of the metal-enriched intra-cluster plasma (ICP) in clusters of galaxies. Rich clusters are considered to constitute a representative sample of the universe, while at the same time - given their deep gravitational potential - they are to be considered from a chemical point of view as closed boxes (all metals produced by cluster galaxies are kept inside the cluster itself).
The mass of metals in the ICP plasma is easily evaluated from the total
amount of ICP baryons (measured to be ![]() 5 times larger than the mass in galactic stars)
and from their average metallicity,
5 times larger than the mass in galactic stars)
and from their average metallicity, ![]() 40% solar. The mass of ICP metals
is Mmetals, ICP
40% solar. The mass of ICP metals
is Mmetals, ICP ![]() 5 × 0.4 (Z/Z
5 × 0.4 (Z/Z![]() ) Mstars, which is
two times larger than the mass of the metals present in galactic stars
and consistent with the mass in metals produced during the SB phase.
) Mstars, which is
two times larger than the mass of the metals present in galactic stars
and consistent with the mass in metals produced during the SB phase.
Then the same starbursts producing the ICP metals are also likely responsible for the origin of the CIRB. As mentioned, the starburst enrichment process could have been pictured in a deep SCUBA image of the candidate proto-cluster surrounding the z = 3.8 radio-galaxy 4C41.17. In a similar fashion, Mushotzky & Loewenstein (1997) used their metallicity measurements in clusters to estimate the contribution of spheroidal galaxies to the SFR density (see Fig. 14).
13.2.4. A two-phase star-formation: origin of galactic disks and spheroids
The above scheme, best-fitting the available IR data as discussed in Sect. 11, implies that star formation in galaxies has proceeded in two phases: a quiescent one taking place during most of the Hubble time, slowly building stars with standard IMF from the regular flow of gas in rotational supported disks; and a transient actively starbursting phase, recurrently triggered by galaxy mergers and interactions. During the merger, violent relaxation redistributes old stars, producing de Vaucouleur profiles typical of galaxy spheroids, while young stars are generated following a top-heavy IMF.
Because of the geometric (thin disk) configuration of the diffuse ISM and the modest incidence of dusty molecular clouds, the quiescent phase is only moderately affected by dust extinction, and naturally originates most of the optical/NIR background (included early-type galaxies completely deprived of an ISM).
The merger-triggered active starburst phase is instead characterized by a large-scale redistribution of the dusty ISM, with bar-modes and shocks, compressing a large fraction of the gas into the inner galactic regions and triggering formation of molecular clouds. As a consequence, this phase is expected to be heavily extinguished and the bulk of the emission to happen at long wavelengths, naturally originating the cosmic CIRB background. Based on dynamical considerations, we expect that during this violent SB phase the elliptical and S0 galaxies are formed in the most luminous IR SBs at higher-z (corresponding to the SCUBA source population), while galactic bulges in later-type galaxies likely originate in lower IR luminosity, lower-z SBs (the ISO mid-IR population).
The presently available IR data cannot assess if the different luminosity ranks of SCUBA and ISO selected sources are characterized also by different formation timescales (SF activities being confined to the higher-z for the former and to lower-z for the latter), since the present samples are far dominated by K-correction and selection effects. Assumed however this is indeed the case, this could still be reconciled with the expectations of hierarchical clustering models if we consider that SCUBA sources likely trace the very high-density (galaxy clusters) environment with an accelerated merging rate at high-z, while ISO sources are likely related with lower-density environments (galaxy groups or the field) entering the non-linear collapse phase at later cosmic epochs (e.g. Franceschini et al. 1999).
Finally, if indeed the IMF characteristic of the SB phase is deprived of low-mass stars, as suggested in the previous paragraphs, a consequence would be that the excess blue stars formed during the SB would quickly disappear, leaving the colors of the emerging remnant as typically observed for early-type galaxies and keeping consistent with the evidence that the stellar mass content in galaxies does not change much for z < 1.
13.3. Contribution by gravitational accretion to the global energetics
The remarkable similarities between the cosmic evolution of galaxy and AGN emissivities have been taken as evidence that the same processes triggering SF also make a fraction of the gas to accrete and fuel the AGN (Hasinger Franceschini et al. 1999). Furthermore, detailed studies of local high-luminosity IR galaxies are showing that SF and AGN activities happen very often concomitantly in the same object (Genzel et al. 1998; Risaliti et al. 2000; Bassani et al. 2000). After all, this is a natural outcome of the scheme discussed in previous Sections, the violent radial inflow of gas following the merger/interaction should likely fuel not only nuclear star-clusters, but the BH itself at some stage.
Waiting for forthcoming and future powerful instrumentation (X-ray observatories CHANDRA and XMM, Constellation-X and XEUS in the future, and large space IR observatories like NGST and FIRST) to have a detailed quantification of the relative merits of the two fundamental baryon drivers, some order-of-magnitude estimates may be useful as a guideline. From a combined analysis of the AGN and starburst average bolometric emissivities as a function of redshift, Franceschini et al. (1999) infer a relationship between the mass MBH of the local remnant super-massive BH after the AGN phase to the mass M * in galactic stars from the SB phase:
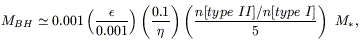
| (13.35) |
where ![]() is the radiative efficiency by BH accretion and
n[type II] / n[type I]
is the ratio of the absorbed to unabsorbed AGNs (which should be close to
3-5 to explain the local AGN statistics and the observed intensity of
the XRB).
On the other hand, observations of supermassive BH's in local spheroidal
galaxies
(Magorrian et al. 1998,
Faber et al. 1997)
indicate a quite higher mass in the BH accreted material
with respect to that in stars: MBH
is the radiative efficiency by BH accretion and
n[type II] / n[type I]
is the ratio of the absorbed to unabsorbed AGNs (which should be close to
3-5 to explain the local AGN statistics and the observed intensity of
the XRB).
On the other hand, observations of supermassive BH's in local spheroidal
galaxies
(Magorrian et al. 1998,
Faber et al. 1997)
indicate a quite higher mass in the BH accreted material
with respect to that in stars: MBH ![]() (0.002 - 0.006) M * .
Assumed that
(0.002 - 0.006) M * .
Assumed that ![]() should not be lower than
0.1, this may require a stellar mass-energy conversion efficiency
should not be lower than
0.1, this may require a stellar mass-energy conversion efficiency
![]() >> 0.001,
which is further independent support to the idea of a top-heavy IMF
during the SB phase.
>> 0.001,
which is further independent support to the idea of a top-heavy IMF
during the SB phase.