High-Redshift Galaxies: The Far-IR and Sub-Mm View

8. THE BREAKTHROUGHS: DISCOVERY OF THE CIRB

Cosmological background radiations are a fundamental channel of information about cosmic high-redshift sources, particularly if, for technological limitations, observations of faint sources in a given waveband are not possible. This was clearly the case for the IR/sub-mm domain. The present Section is dedicated to a review on a recently discovered new cosmic component, the cosmological background at IR and sub-millimetric wavelengths (CIRB), an important achievement made possible by the NASA's Cosmic Background Explorer (COBE) mission.

To appreciate the relevance of this discovery (anticipated by a detailed modellistic prediction by Franceschini et al. 1994), consider that extragalactic backgrounds at other wavelengths contain only modest (undiscernible) contributions by distant galaxies. The Radio background is clearly dominated by radio-loud AGNs; the Cosmic Microwave Background includes photons generated at z $\sim$ 1500; the X-ray and $\gamma$ -ray backgrounds are dominated by distant quasars and AGNs. Also, diffuse light in the optical-UV (and partly the near-IR) will be hardly depurated of the foreground contaminations (in particular, Galactic starlight reflected by high latitude "cirrus" dust, and Zodiacal-reflected Sun-light).

On the other hand, the recently completed third experiment (DIRBE) of the COBE mission has brought to the first detection ever (with surprisingly small uncertainties) of the integrated emission of distant galaxies in the form of an isotropic signal in the far-IR and sub-mm (Puget et al. 1996, Guiderdoni et al. 1997, Hauser et al. 1998, Fixsen et al. 1998).

8.1. Observational status about the CIRB

In spite of the presence of very bright foregrounds (Zodiacal and Interplanetary dust emission, Galactic Starlight, high-latitude "cirrus" emission), relatively clean spectral windows exist in the IR suitable for extragalactic research: the near-IR cosmological window (2-4 µm) and the sub-mm window (100-500 µm). At these wavelengths the Zodiacal, Starlight, and emission by high galactic latitude dust produce two minima in the total foreground intensity, which is much lower here than it is in the optical-UV.

These spectral windows occur where we would expect to observe the redshifted photons from the two most prominent galaxy emission features: the stellar photospheric peak at $\lambda$ $\sim$ 1 µm and the one at $\lambda$ $\sim$ 100 µm due to dust re-radiation. The best chances to detect the integrated emission of distant and primeval galaxies are here.

For a curious coincidence, the (expected) integrated emission of distant galaxies turns out to be comparable by orders of magnitude to the Galaxy emission at the Pole and to the Zodiacal light in the near-IR window. This implies that a delicate subtraction of the foreground emissions is required to access the extragalactic domain.

Three main observational routes have been followed to measure the CIRB:

rocket flights of dedicated instrumentation (1970-1990), now only of historical interest;
all-sky surveys by space telescopes (IRAS and COBE, 1984-1996);
indirect estimates based on very high-energy spectral observations of extragalactic $\gamma$ -ray sources (Stecker, de Jager & Salomon 1992; Stanev & Franceschini 1998).

In sky directions outside obvious Galactic sources, like star-forming and low-galactic latitude regions, the total far-IR background is due to the contribution of various dust components in the ISM: galactic dust associated with neutral and ionized hydrogen, the interplanetary dust emission, all adding to the isotropic diffuse flux, the CIRB. The way to subtract these various foregrounds when estimating the CIRB intensity is to exploit the different spatial dependencies of the various components, using the correlations with appropriate dust tracers like the HI 21 cm or H lines.

To subtract the most important foreground in the far-IR, the galactic dust emission, the simplest procedure is to determine the parameters of the correlation between the background intensity I and the dust tracers expressed in terms of equivalent hydrogen column density N_H, and then to evaluate the CIRB as the intercept of the total flux at N_H = 0.

Another method is to perform an all-sky best-fit analysis of a relation like I = C₁N_H(HI) + C₂N_H(II) + CIRB, N_H being the column densities of the dust components associated with the neutral and ionized H, CIRB being the extragalactic background intensity at the working wavelength (e.g, Lagache et al. 1999). The best-fitting determines the constant C₁and C₂ and allows to estimate a value for the parameter CIRB.

Puget et al. (1996) first recognized in the all-sky FIRAS/COBE maps an isotropic signal (independent of Galactic coordinates) with an intensity that can be represented by the law $\nu$ B $\simeq$ 3.4 × 10^-9( $\lambda$ /400µm)^-3 W m^-2 sr^-1 in the 400-1000 µm interval.

This tentative detection has been later confirmed with independent analyses by various other groups (e.g. by Fixsen et al. 1998, who find significant isotropic signal from 200 and 1000 µm), as well as by analyses of data from the DIRBE experiment on COBE in two broad-band channels at $\lambda$ = 140 and 240µ (Hauser et al. 1998). Finkbeiner, Davies & Schlegel (2000), after a very delicate subtraction of the far dominant Galactic and IPD foregrounds, found an isotropic signal at 60 and 100 µm with intensity at the level of $\sim$ 30 10^-9 W m^-2 sr^-1. This latter result is presently under discussion, but appears to conflict with independent estimates (see Sect. 8.2).

Recent analyses by Dwek & Arendt (1998) and Gorjian, Wright & Chary (2000) have tentatively found also a signal in the near-IR cosmological window at 3.5 µm and in the J, H and K DIRBE bands, however with large uncertainties because of the problematic evaluation of the Zodiacal (scattered) light. Because of this, CIRB estimates particularly in J, H and K are to be taken more reliably as upper limits.

To avoid overcrowding, we report in Figure 3 only the most recent results from DIRBE (Lagache et al. 1999; Finkbeiner, et al. 2000) and FIRAS (Fixsen et al. 1998).

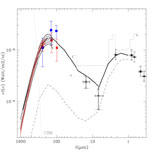
Figure 3. The Cosmic Infrared Background (CIRB) as measured by independent groups in the all-sky COBE maps (e.g. Hauser et al. 1998), compared with the optical extragalactic background estimated from ultradeep optical integrations by the HST in the HDF (Madau & Pozzetti 2000). Three datapoints in the far-IR are from a re-analysis of the DIRBE data by Lagache et al. (1999), the shaded area from Fixsen et al. (1998) and Lagache et al. The two mid-IR points are the resolved fraction of the CIRB by the deep ISO surveys GITES, while dashed lines are limits set by TeV cosmic opacity (Sect. 8.2). The dotted line marks the expectation based on the assumption that the IR emissivity of galaxies does not change with cosmic time. The thick line is the predicted CIRB intensity by the model discussed in Sect. 11.

No isotropic signals are significantly detected at 4µ < $\lambda$ < 60µ, any cosmological flux being far dominated here by the Zodiacal light, the Interplanetary dust (IPD) emission and by Galactic dust emission (only missions to the outer Solar System would have chances to reduce the dominant IPD flux to achieve detection of the CIRB here). The constraints we report at these wavelengths come from indirect estimates based on the cosmic high-energy opacity (Sect. 8.2 below).

Altogether, after four years of very active debate among various teams working on the COBE data, first about the existence and later on the intensity and spectral shape of CIRB, there is now ample consensus even on details of CIRB's spectral intensity, at least from 140 to 300 µm where it is most reliably measured and where two completely independent datasets (FIRAS and DIRBE, with independent absolute calibrations) are available. The CIRB flux has in particular stabilized at values $\nu$ I $\simeq$ 24±5 and $\nu$ I $\simeq$ 15±5 10^-9 Watt/m²/sr at $\lambda$ = 140 and 240 µm. Modest differences in the absolute calibration of FIRAS and DIRBE around 100 µ have been reported (Hauser et al. 1998), but these do not seem to affect the overall result.

This was a fundamental achievement for observational cosmology, providing the global energy density radiated by cosmic sources at any redshifts. Two concomitant facts, the very strong K-correction for galaxies in the far-IR/sub-mm implied by the very steep and featureless dust spectra, and their relative robustness due to the modest dependence of dust equilibrium temperature T on the field intensity (eq. 3.6]) have suggested to use the CIRB spectrum to infer the evolution of the galaxy long-wavelength emissivity as a function of redshift (Gispert, Lagache & Puget 2000). Indeed, while the peak intensity at $\lambda$ = 100 to 200 µm constrains the galaxy emissivity at z = 0 to z = 1, the quality of the FIRAS intensity maps and the low foreground contamination at $\lambda$ > 200 µm allow to set important constraints on the universal emissivity at z > 1.

Between 100 and 1000 µm the integrated CIRB intensity turns out to be $\sim$ 30±5 10^-9 Watt/m²/sr. In addition to this measured part of the CIRB, one has to consider the presently un-measurable fraction resident in the frequency decade between 100 and 10 µm. This flux is larger than the integrated "optical background" ( $\sim$ 17 nWatt/m²/sr, see Fig. 3), obtained by counting all galaxies detected between 0.3 and 3 µm by HST down to the faintest detectable sources. This procedure to estimate the "optical background" relies on the fact that optical counts show a clear convergence at magnitudes m_AB $\geq$ 22 (Madau & Pozzetti 2000), such that the expected contribution by sources fainter than HST limiting fluxes appears negligible (a significant upwards revision of this optical background suggested by Bernstein et al. [1998] to account for low surface brigtness emission by galaxies is not confirmed).

Already the directly measured part of the CIRB sets a relevant constraint on the evolution of cosmic sources, when compared with the fact mentioned in Sect. 4.2.5 that for local galaxies only 30% of the bolometric flux is absorbed by dust and re-emitted in the far-IR. The CIRB's intensity matching or even exceeding the optical background tells unequivocally that galaxies in the past should have been much more "active" in the far-IR than in the optical, and very luminous in an absolute sense. A substantial fraction of the whole energy emitted by high-redshift galaxies should have been reprocessed by dust at long wavelengths.

8.2. Constraints from observations of the cosmic high-energy opacity

As originally suggested by F. Stecker soon after the discovery of high-energy photon emissions from distant blazars, high-energy spectral observations may provide a suitable alternative to the direct detection of the CIRB at wavelengths where it is currently impossible. The idea is to infer the CIRB intensity from combined GeV and TeV observations of a set of Blazars by exploiting the $\gamma$ $\rightarrow$ $\gamma$ interaction of their emitted high energy photons with those of the CIRB.

The absorption cross-section of $\gamma$ -rays of energy E [TeV] has a maximum for IR photons with energies obeing the condition (Stecker, de Jager & Salomon 1992):

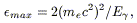
which implies

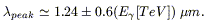
(8.15)

The optical depth for a high-energy photon E₀ travelling through a cosmic medium filled of low-energy photons with density $\rho$ (z) from z_e to the present time is

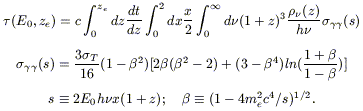
(8.16)

Coppi & Aharonian (1999) report the following analytical approximation, good to better than 40%, to eq. (8.16):

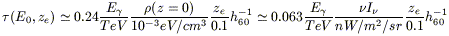
(8.17)

Interesting applications of this concept have been possible when data from the Compton Gamma Ray Observatory and from hard X-ray space telescopes have been combined with observations at TeV energies by the Whipple and other Cherenkov observatories on the Earth.

Stanev & Franceschini (1998) have obtained model-independent upper limits on the CIRB with no a-priori guess about the CIRB spectrum, using HEGRA data for the Blazar MKN 501 (z = 0.034) during an outburst in 1997, on the assumption that the high-energy source spectrum is the flattest allowed by the data. These limits (see Fig. 3) get quite close to the CIRB background already resolved by the ISO mid-IR deep surveys (see Sect. 9).

More recently, Krawczynski et al. (1999) have combined the observations of MKN501 during the 1997 outburst with X-ray data from RossiXTE and BeppoSAX, providing a simultaneous high-quality description of the whole high-energy spectrum. These data are very well fitted by a Synchrotron Self Compton (SSC) model in which the spectrum at $\nu$ = 10²⁷Hz is produced by Inverse Compton of the hard X-ray spectrum at $\nu$ = 10¹⁸Hz: the combination of the two provides solid constraints on the shape of the "primary" (i.e. before cosmic attenuation) spectrum at TeV energies. This is used to derive $\tau_{\gamma\gamma}^{}$ as a function of energy and, after eqs. 8.16 and 8.17, a constraint on the spectral intensity of the CIRB. The result is compatible with the limits by Stanev & Franceschini (1998) and allows to get a tentative estimate of the CIRB intensity in the interval from $\lambda$ = 10 to 40 µm (see Fig. [3]), which is formally dependent, however, on the SSC model adopted for the intrinsic source spectrum.

Less model dependent is the constraint set by the observations of purely power-law Blazar spectra around E $\simeq$ 1 TeV, which translates into the upper limit of about 10 nanoWatt/m²/sr at $\lambda$ $\simeq$ 1 µm shown in Fig. 3. Substantially exceeding that, as suggested by some authors (Bernstein et al., Gorjian et al.), would imply either very "ad hoc" $\gamma$ -ray source spectra or new physics (Harwit, Proteroe & Bierman 1999).

8.3. Contribution of cosmic sources to the CIRB: the formalism

A simple formalism relates background intensity and cell-to-cell anisotropies to the statistical properties (luminosity functions and number counts) of the contributing sources.

8.3.1. Source contribution to the background intensity

The differential number counts (sources/unit flux interval/unit solid angle) at a given flux S write:

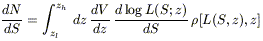
(8.18)

where $\rho$ [L(S, z), z] is the epoch-dependent luminosity function and dV/dz is the differential volume element. Flux S and rest-frame luminosity L are related by

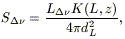
(8.19)

where d_L is the luminosity distance and K(L, z) = (1 + z) ${L[\nu (1+z)]\over L(\nu)}$ the K-correction. The contribution of unresolved sources (sources fainter than the detection limit S_d) to the background intensity is given by:

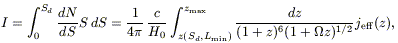
(8.20)

having defined the volume emissivity j_eff(z) as

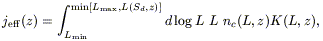
(8.21)

where L_min and L_max are the minimum and the maximum source luminosities. From eq. (8.20) we can note that, when the counts converge like dN/dS $\propto$ S^-2 or flatter, the contribution by faint sources to the background intensity becomes almost insensitive to the source minimum flux [I $\propto$ ln(S_min) or less]. This property has been used by Madau & Pozzetti (2000) to estimate the optical background intensity (see Fig. 3) from ultra-deep HST counts of galaxies, by exploiting the convergence of the optical counts fainter than m_AB $\sim$ 22. A similar property of faint IR sources is used in Sect. 9.4 to estimate the contribution of IR galaxies to the CIRB.

8.3.2. Small scale intensity fluctuations

In addition to the average integrated flux by all sources in a sky area, the background radiation contains also spatial information (the cell-to-cell fluctuations) which can be used to further constrain the source flux distribution and spatial correlation properties (e.g. De Zotti et al. 1996). The usually most important contribution to the cell-to-cell intensity fluctuations comes from the stochastic nature of the spatial distribution of sources among elementary cells with an effective solid angle $\omega_{\rm eff, P}^{}$ (Poisson fluctuations). They can be expressed as

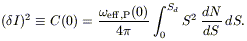
(8.22)

What is really measured, however, is not the flux S but the detector's response x = f ( $\vartheta$ , $\varphi$ )S, f ( $\vartheta$ , $\varphi$ ) being the angular power pattern of the detector. Let R(x) = $\int$ dN $\left[\vphantom{x/f(\vartheta , \varphi )}\right.$ x / f ( $\vartheta$ , $\varphi$ ) $\left.\vphantom{x/f(\vartheta , \varphi )}\right]$ / dS^.d $\omega$ /f ( $\vartheta$ , $\varphi$ ) be the mean number of source responses of intensity x. For a Poisson distribution of the number of sources producing a response x, its variance equals the mean R(x)dx. Adding the variances of all responses up to the cutoff value x_c (brighter sources are considered to be individually detected) gives the contribution of unresolved sources to fluctuations:

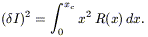
(8.23)

The cutoff x_c is chosen to be some factor q times ( $\delta$ I)²; usually q = 3-5. The rms background fluctuations ( $\delta$ I) imply a sky noise $\sigma_{conf}^{}$ = $\langle$ ( $\delta$ I)² $\rangle^{1/2}$ for observations with spatial resolution $\omega_{eff}^{}$ .

The integrated signal D recorded by the detector is the sum of the responses x due to all sources in the angular resolution element. Its probability distribution function P(D) is informative on the amplitude and slope of counts of unresolved sources. Scheuer (1957) has shown that its Fourier transform, p( $\omega$ ), is a simple function of the FT r( $\omega$ ) of R(x): p( $\omega$ ) = exp[r( $\omega$ ) - r(0)]. It follows:

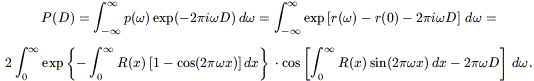
(8.24)

This synthetic P(D) has to be convolved with the noise distribution to be compared with the observations. Assumed that the number count distribution below the detection limit can be represented as a power-law, N( > S) = K(S / S_k)^-, then eq. [8.24] can be integrated to get (Condon 1974):

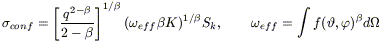
(8.25)

which allows to estimate the slope of the counts ( $\beta$ ) below the detection limit from a given measured value of the cell-to-cell fluctuations $\sigma_{conf}^{}$ . This constraint on N(S) applies down to a flux limit corresponding to $\sim$ 1 source/beam. Assumed that S_k represents the confusion limit (S_k = q × $\sigma_{conf}^{}$ ) of a survey having an areal resolution $\omega_{eff}^{}$ , then eq. 8.25 further simplifies to a relation between the number of sources K resolved by the survey (and brighter than S_k) and the parameters q and $\beta$ :

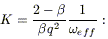
(8.26)

this implies the confusion limit to occur at the flux corresponding to an areal density of ( $\beta$ q²/[2 - $\beta$ ])^-1 sources per unit beam area $\omega_{eff}^{}$ . For euclidean counts and q = 3, this corresponds to 1 source/27 beams. Confusion limits based on this criterion for various IR observatories are indicated in Figs. 6 and 7 below.