3.1. He I and H I Emissivities
The F(He I) / F(H
) emission line
flux ratios are converted to intrinsic intensity ratios, I(He I) /
I(H), by correcting
for reddening and underlying H I absorption and then incorporating
the errors in these corrections (from eq. (2)) into the errors in
the line ratios as discussed in
section 2.2. These intrinsic line ratios
can then be converted to He/H abundance ratios by using the theoretical
emissivities calculated from recombination and radiative cascade theory
(e.g.,
Brocklehurst 1971;
1972).
Here we use the H I emissivities calculated by
Hummer & Storey (1987)
and the He I emissivities calculated by
Smits (1996).
See Appendix C for further details. Normally,
uncertainties in the H I and He I emissivities are not included in the error
calculations when determining He/H abundance ratios. It is usually
assumed that these uncertainties are small in comparison with
the other error terms, however, the quoted uncertainties on
derived nebular helium abundances are becoming so small that this
assumption may no longer be true.
We would like to note that there is still a need for a modern
assessment of the uncertainties of the calculated He I emissivities.
Benjamin, Skillman, &
Smits (1999)
have estimated that the uncertainty in the input atomic data alone may
limit the accuracy to 1.5%.
3.2. Collisional Enhancement of He I Emission Lines
At the high electron temperatures found in metal poor nebulae, collisional excitation from the metastable 2S level can become significant in determining the higher level populations in He I. This effect has an exponential dependence on electron temperature and a linear dependence on density. Thus, the theoretical emissivities need to be "corrected" for the radiative contribution of these collisional excitations. In order to better calculate these collisional corrections to the radiative cascade, quantum calculations of increasing accuracy have been carried out to determine more exact collisional rates (Berrington et al. 1985; Berrington & Kingston 1987; Sawey & Berrington 1993). Here we use the collisional rates of Sawey & Berrington (1993) and the resulting collisional corrections calculated by Kingdon & Ferland (1995). In principle, it is better to join the collisional effects directly into the recombination cascade calculation (e.g., as done by Benjamin et al. 1999), but for the present exercise absolute numbers are less important than judging the relative magnitudes of various effects. One of the original motivations for this work was to reproduce the results published in IT98, so we have adopted an identical treatment of the input atomic data.
3.3. The Effects of Underlying Stellar Absorption
A potential source of systematic error is the possibility of stellar absorption underlying the helium emission lines. Certainly there are typically many early type stars exciting the observed HII regions, and certainly many of these stars have strong He I absorption lines.
Judging the
degree to which underlying stellar absorption is important
has been a real problem in the past (e.g.,
Shields & Searle 1978).
Kunth & Sargent (1983)
proposed the very simple test of looking for
a trend in derived He abundance with EW(He I emission).
They found no evidence for this effect in their data (which span
approximately the same range in EW(He I emission) as modern day
observations).
Skillman, Terlevich, &
Terlevich (1998)
reexamined their data and found evidence for a slight trend in He/H
with EW(H) implying that
underlying absorption may be
present at a detectable level. The theoretical modeling results of
Olofsson (1995)
have also been used as a guide in the past.
These models indicated that the
EW of 
4471 in absorption
was generally of order 0.1 Å or less. However,
Skillman, Terlevich, &
Terlevich (1998)
pointed out that the model results may not be
representative of the typical extragalactic HII region observed
for these purposes, and that the
underlying absorption values may be much larger than 0.1.
They also drew attention to an inconsistency in the relative
strengths of He I absorption lines modeled by Olofsson. That is, in
observed stars (e.g.,
Lennon et al. 1993)
and in numerical models (e.g.,
Auer & Mihalas 1972),
the strengths of the 4471 and
4026 lines are about a
factor of two stronger than
4387 and
4922, while in the models
of Olofsson, the opposite is true. This potentially implies that the
underlying absorption in
4471 and
4026
could have been underestimated by a factor of 4 in Olofsson's
models (EWs for 5876 and
6678 are not calculated).
Revisiting the modeling by Olofsson with a view to the specific case
of determining nebular helium abundances remains a valuable
exercise for the future.
What are the greater implications for this realization that the effects of underlying absorption could have been underestimated in the past? Izotov & Thuan (1998a) have demonstrated that underlying absorption is important in the NW component of I Zw 18. IT98 recognize the potential importance of underlying stellar absorption. They deal with this effect by (1) averaging over three lines or (2) excluding a line from consideration when "absorption is evidently important".
Here, we feel that a truly self-consistent approach will account
for the effects of underlying absorption through detection and
correction for such effects.
In the next section we present a method for doing this.
We pursue two different methods; first we include the
possibility of underlying absorption in a
2 minimization
routine. Second, we experiment with including a sixth line
4026, which has enhanced
sensitivity to underlying absorption.
In order to do this correctly, one must know, a priori, the
relative strengths of the underlying He I absorption lines.
We assume that the underlying He I stellar absorption lines
are all equal in terms of equivalent width. Recall that we made a
similar assumption in the case of underlying H I absorption. Similarly,
we cannot estimate how much systematic error we are incurring with this
assumption in the analysis of real observations. However, by making the
same assumption in both the synthesized spectra and the analysis, we can
focus on the uncertainties in the method. The assumption of identical
equivalent widths is probably not too bad.
Observations of individual Galactic B supergiants
(Lennon, Dufton, &
Fitzsimmons 1993)
show that the EW of the absorption lines of
6678,
4471,
and 4026 are all of
approximately equivalent strength
and share the same dependency on stellar effective temperature.
The models by
Auer & Mihalas (1972)
show relatively good
agreement for EW(4026),
EW(4471),
EW(5876), and
EW(6678) for temperatures
in excess of 35,000 K and surface gravity values values of log g = 4
and 4.5.
3.4. He I Optical Depth Effects
In order to compare observational measurements of helium
line intensities with theoretical values, it is necessary to
consider radiative transfer effects and
to determine what effects these have on the resulting line ratios.
The standard references for radiative transfer in He I emission
lines are those of
Robbins (1968) and
Robbins & Bernat (1973).
Recent examinations of this issue are given by
Almog & Netzer (1989),
Proga, Mikolajewska, &
Kenyon (1994) and
Sasselov & Goldwirth
(1995).
Given the
improvements in the atomic data afforded by the re-examination of
A-values
(Kono & Hattori 1984),
the recombination rates
(Smits 1996),
and collisional rates
(Sawey & Berrington
1993),
a re-examination of radiative transfer issues should be very useful.
For the purpose of reproducing the IT98 results, here we will adopt the
fits given by IT98 to the modeling results of
Robbins (1968)
(the IT98 equations are reproduced in
Appendix C). In
Figure 3 we show the data from
Robbins (1968)
and the IT98 fits. Note that for the regime of low values of
(3889) relevant for the
current study (values of (3889)
2 
2 1.5 are rarely observed)
there is very little data available from
Robbins (1968).
It is also important to note that these results represent only one
set of physical conditions. An important parameter is the
velocity gradient of the absorbing gas, which has been assumed to
be zero in the models chosen by IT98.
This is further motivation for a new study of the He I radiative
transfer effects.
|
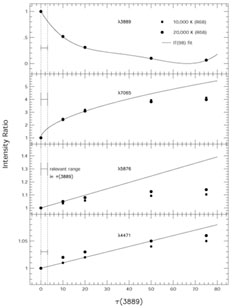
Figure 3. Graphs showing the IT98 fits to the
florescence enhancement figures reported in
Robbins (1968).
The important point to note is that regime of the calculations
is mostly at far larger values of
|
3.5. Ionization Correction Factors
The degree to which the hydrogen and helium ionization zones in an HII region coincide is generally determined by the hardness of the ionizing radiation field, and may be governed, in part, by geometry (e.g., Osterbrock 1989). Thus, there is always concern that in a specific observation of an HII region that neutral helium is co-existent with ionized hydrogen along the line of sight (see, e.g., discussion in Dinerstein & Shields 1986).
Historically, a correction has been applied to the helium abundances in order to correct for unobserved neutral helium. Vílchez & Pagel (1988), following the ideas of Mathis (1982), used the models of Stasinska (1990) to demonstrate that ratios of ionization fractions of sulfur and oxygen provided an accurate measure of the hardness of the radiation field. Pagel et al. (1992) used this technique to determine whether such a correction was necessary. Their proposed methodology consisted of a simple test: if the radiation field was soft enough that a significant correction for neutral helium was implied, this correction was probably too uncertain for the proposed candidate to be useful for a helium abundance measurement.
ITL94 and ITL97 applied neutral helium corrections based on the models of Stasinska (1990), without adopting the methodology of PSTE. Unfortunately, the correction derived in ITL94 is based only on the neutral helium fraction and does not take into account the neutral hydrogen fraction (see discussion in Skillman, Terlevich, & Terlevich 1998). IT98 revised these estimates assuming ionization correction factors of one.
Viegas, Gruenwald, & Steigman (2000) have produced photoionization models indicating that H II regions ionized by young, hot, metal-poor stars may actually have more extended ionized helium regions when compared to the ionized hydrogen. This results in a "reverse" ionization correction, reducing the derived helium abundance by as much as 1% (cf. Figure 2 in Skillman, Terlevich, & Terlevich 1998). At present, lacking observational evidence of this effect, it is not clear that such a correction should be applied, but the fact that it is of order the size of the errors presently quoted on derived helium abundances implies that it should not be ignored in the error budget.
In this work we will simply assume that the ionization correction factors are very close to one. Skillman et al. (1994) noted the constancy of He/H as a function of position in UGC 4483 despite significant variations in oxygen ionization ratios. However, it is very difficult to constrain this uncertainty to less than 1%.