The last two decades have seen a tremendous growth in our awareness of the richness of the structure of the Universe on scales of galaxies and larger. Technical advances in spectrographs and detectors in both the visible and radio wavebands have allowed redshifts of large numbers of galaxies to be measured efficiently, giving us the opportunity to map their distribution for the first time. We are in the midst of a golden age of exploration. The redshift surveys of the last fifteen years have discovered the existence of superclusters, great voids, and coherent structures stretching across the entire volume covered by the surveys. But it is not just "geography" (or cosmography, as it is called in the astronomical context) that has been done: hidden in the statistics of the galaxy distribution is much important information about the structure of the Universe on large scales. Thus we can deduce much about the early history of the universe, and its global structure, from careful quantitative analyses of redshift surveys: this will be the central theme of this review.
The Hubble Law states that at distances much less than the Hubble radius, the expansion of the universe causes the recession velocity of a galaxy cz to be proportional to its distance r:
| (1) |
where H0 is the Hubble Constant, whose value
remains uncertain by a factor of two; in astronomer's units, it is often
written as
H0 = 100h km s-1
Mpc-1, the quantity h
parameterizing our ignorance of its value. Mpc stands for megaparsecs,
the common unit of distance for much extragalactic work:
1 Mpc = 3.08 × 1024 cm. Thus in
physicist's units, H0 = 3.25 × 10-18
h sec, or H0-1
1010
h-1 yr.
In practice, we will rarely be troubled by the uncertain value of h
in this review, because we will measure distances in units of
km s-1, wherein
H0 
1. The
observational evidence for the linearity of Eq. (1) is reviewed in
Peebles (1993)
and
Lauer & Postman (1992)
;
cf. Section 3.6 below.
At the low redshifts discussed in the majority of this review, relativistic effects are for the most part unimportant and the Hubble law is an excellent approximation. However, galaxies have motions above and beyond their Hubble velocities, deviations from the isotropic expansion that holds only in the theoretical idealization of a perfectly homogeneous universe. Thus Eq. (1) is modified to:
| (2) |
where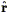 
is the unit vector towards the
galaxy in question,
v(r) is the peculiar velocity at position
r, and
v(0) is the peculiar velocity of the observer. The
development over the past fifteen years of redshift-independent
methods of measuring distances have allowed the measurement of the
peculiar velocity field v(r). As we will see in detail,
observations of the peculiar velocity field are of great importance;
it is their study which occupies the second half of this review. In
particular, under the hypothesis that structure formed by the
gravitational growth of small perturbations on an initially uniform
background, there is a direct relation between the density and
velocity fields, which we will exploit to great
advantage to put constraints on cosmological models.
Thus the main emphasis in this review will be on quantitative constraints that can be placed on cosmological models, from redshift and peculiar velocity surveys of the local Universe. By local, we mean at distances small compared with the horizon distance, or equivalently, at look-back times small relative to the age of the universe, or redshifts small compared to the speed of light. That is, for most of this review, we will not be concerned about the general relativistic generalization of Eq. (1), and can work in the Newtonian limit almost exclusively. Another definition of the local universe is that within which evolutionary effects in the galaxy properties can be assumed to be negligible. In practice, we will restrict ourselves to recession velocities below 20,000 km s-1 (z = 0.067).
There are a number of major reviews and books that are relevant as background material for this review. The reader is assumed to be familiar with the basics of Big Bang cosmology, as reviewed in Peebles (1993) and Padmanabhan (1993) . Somewhat more advanced material can be found in White (1991) , Efstathiou (1991) , and Suto (1993) . Older texts that also discuss this material include Peebles (1971) , Efstathiou & Silk (1983) , Peebles (1980) and Weinberg (1972) . A useful pocket summary of the field is found in Scott et al. (1994) . We will many times skirt the issues of astroparticle physics in the cosmological context; Kolb & Turner (1990) is an excellent overview of the field. Redshift surveys are discussed in Geller & Huchra (1988) and Giovanelli & Haynes (1991) , and peculiar velocity surveys are reviewed in Burstein (1990) and Dekel (1994) . The subject can also be followed in the proceedings of many conferences, among them Brück, Coyne, & Longair (1982) , Kolb et al. (1986) , Madore & Tully (1986) , Burbidge & Hewitt (1986) , Kormendy & Knapp (1987) , Audouze, Pellatan, & Szalay (1987), Rubin & Coyne (1988) , van den Bergh & Pritchet (1988) , Latham & da Costa (1991), Chincarini et al. (1993) , and Bouchet & Lachiéze-Rey (1993).
We stress observational aspects of large-scale structure studies in this review. Not all aspects of the field can be covered. In particular, we only touch upon observations of the high-redshift universe, either in galaxies (Spinrad & Kron 1995 ) or in background radiation (Partridge 1994 ). We focus exclusively on galaxies as probes of large-scale structure, and do not discuss the distribution of clusters of galaxies (e.g., Bahcall 1988 ). See the review of Efstathiou (1994) for a more unified treatment of the large-scale distribution of galaxies and clusters. We also do not review evidence for dark matter on Galactic scales (Faber & Gallagher 1979 ; Trimble 1987 ; Binney & Tremaine 1987 ), or models for galaxy formation (e.g., White 1994 ). Finally, although peculiar velocities are a major focus of this paper, we do not review the closely related question of the determination of the Hubble Constant (cf. Jacoby et al. 1992 ).
This review is too long to be read in a single sitting, but the different chapters are largely independent. Chapter 2 covers the basics of Big Bang cosmology to the extent needed for the rest of the review, and can be skipped by the reader familiar with this material. Chapter 3 gives a history of redshift surveys, and discusses many of the practical issues needing to be addressed in their quantitative analysis. Chapter 4 is a qualitative tour of the structures we see within 8000 km s-1, as revealed to us via redshift surveys. Those who are interested in quantitative results can skip ahead to Chapter 5, which details the various statistical measures of large-scale structure that have been drawn from redshift surveys.
We then shift the focus to peculiar velocity surveys. Chapter 6 parallels Chapter 3 and discusses the practical aspects of peculiar velocity measurements. We put special emphasis on the various biases which plague peculiar velocity work, and the methods necessary to correct them. Quantitative analyses of peculiar velocity surveys are discussed in Chapter 7, and analyses of redshift and peculiar velocity surveys together are covered in Chapter 8. Chapter 9 is a summary chapter.
Those readers who are familiar with much of the background material may thus find it most useful to read Chapters 5, 7, and 8, after skimming Chapters 3 and 6. We recommend that students new to the field read through the entire review, making sure that they understand the basic concepts introduced in Chapter 2.