


2.2.2. Rotational properties
The nearby stars in the disc of our own galaxy have very small random
velocities ( 30
km/sec) compared to the local rotational velocity
(
30
km/sec) compared to the local rotational velocity
( 250 km/sec). It seems
reasonable to assume that the discs of external
galaxies are cold in analogy with our own disc. Further, because discs
are thin, large random motions are only possible if the velocity
dispersions are highly anisotropic.
250 km/sec). It seems
reasonable to assume that the discs of external
galaxies are cold in analogy with our own disc. Further, because discs
are thin, large random motions are only possible if the velocity
dispersions are highly anisotropic.
For a cold disc, the rotation curve may be determined uniquely from the surface density (Toomre, 1963). Thus the rotation curve of a disc galaxy may be used together with surface photometry to check for radial variations in the mass-to-light ratio. The rotation curve expected for an exponential disc is shown in Figure 2.4. Note that at large radii, the rotation velocity falls approximately as r-1/2.
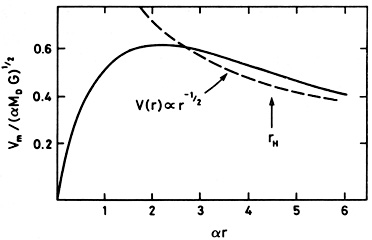 |
Figure 2.4. The solid line shows the
rotation curve of a cold
exponential disc. The dashed line shows the Keplerian velocity law
v(r) |
Extended rotation curves have been observed for a number of galaxies using both 21 cm and optical emission lines (e.g. Bosma, 1978), and references therein; Rubin et al., 1980). The rotation curves do not show the predicted fall at large radii, rather they remain approximately constant out to the limits of detectability, which usually corresponds to a radius close to the Holmberg radius rH. (3) There are two possible interpretations of this result. If the matter is distributed in a disc, a constant rotational velocity vm implies a surface density,
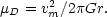 |
(2.13) |
Alternatively, if most of the matter at large radii is distributed spherically, then the density must vary as,
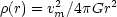 |
(2.14) |
There are few direct observational arguments which may be used to distinguish between these possibilities. However, in either case, the mass enclosed within radius r increases as,
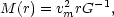 |
(2.15) |
Because Eq. (2.15) diverges with increasing radius it is possible that a large fraction of the total mass in the universe may be in a dark component located in the outer parts of galaxies (but see Kalnajs, 1983).
At present it is not at all clear what the dark matter might be. The
flat rotation curves may imply that the stellar population within the
disc changes with radius, the dark matter may then be in dead remnants
of massive stars, or in low mass stars
( 0.1
M
0.1
M ).
Alternatively, the
dark matter may be a separate dynamical component composed, say, of
massive neutrinos or stellar remnants and may have formed in a
completely different way from the disc.
).
Alternatively, the
dark matter may be a separate dynamical component composed, say, of
massive neutrinos or stellar remnants and may have formed in a
completely different way from the disc.
Equation (2.15) may be used to obtain the mass-to-light ratio within
the Holmberg radius. The results indicate a correlation with
morphological type
(Faber and Gallagher,
1979)
with late-type galaxies (Sc-Sm) having M/LB
 8h and
early-type discs (Sa) having M/LB
8h and
early-type discs (Sa) having M/LB
 20h.
The correlation is in the sense expected from simple models of stellar
populations and star formation rates
(Larson and Tinsley,
1978).
20h.
The correlation is in the sense expected from simple models of stellar
populations and star formation rates
(Larson and Tinsley,
1978).
21-cm line profiles have been obtained for a large number of disc galaxies. The line width provides a measure of vm and of the total mass within the Holmberg radius via Eq. (2.15). Tully and Fisher (1977) find a correlation between the total blue-luminosity (LB)T (corrected for internal and Galactic absorption) and vm
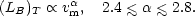 |
(2.16) |
Since Freeman's law requires rH
 LD1/2, the Tully-Fisher relation implies that
LD1/2, the Tully-Fisher relation implies that
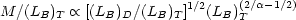 |
(2.17) |
(the subscript D refers to the disc luminosity and the subscript
T refers to the total luminosity, disc + bulge). Since for late-type
discs (LB)D /
(LB)T
 1, the Tully-Fisher
relation shows that the
mass-to-light ratio increases with increasing luminosity.
1, the Tully-Fisher
relation shows that the
mass-to-light ratio increases with increasing luminosity.
Aaronson et al. (1979)
have examined the correlation between
infrared luminosity (LH)T and
vm. They find a relation
(LH)T
 vm4.
According to Eq. (2.17) this implies M /
(LH)T
vm4.
According to Eq. (2.17) this implies M /
(LH)T
 [(LB)D /
(LH)T]1/2,
thus Aaronson et al. conclude that M /
(LH)T remains approximately
constant for late type galaxies. Recently,
Burstein et al. (1982)
have analysed rotation curve data for a sample of 21 Sc galaxies measured
by Rubin et al. (1980).
They find a relation (LB)T
[(LB)D /
(LH)T]1/2,
thus Aaronson et al. conclude that M /
(LH)T remains approximately
constant for late type galaxies. Recently,
Burstein et al. (1982)
have analysed rotation curve data for a sample of 21 Sc galaxies measured
by Rubin et al. (1980).
They find a relation (LB)T
 vm4. This is not
necessarily in conflict with the Tully-Fisher relation as it is based
exclusively on one particular morphological type. As we have
summarized above, mass-to-light ratio appears to correlate with galaxy
type, as does the disc-to-bulge ratio.
vm4. This is not
necessarily in conflict with the Tully-Fisher relation as it is based
exclusively on one particular morphological type. As we have
summarized above, mass-to-light ratio appears to correlate with galaxy
type, as does the disc-to-bulge ratio.
The bulges of some spiral and lenticular galaxies have been studied spectroscopically in some detail (Illingworth and Schechter, 1982; Kormendy and Illingworth, 1982). The results show that the bulges rotate rapidly, consistent with the predictions of the oblate isotropic model (Eq. 2.4). These results are shown as the crosses in Figures 2.2 and 2.3. It is also clear from these diagrams that typical bulges are fainter than typical elliptical galaxies, but that at fixed absolute magnitude there appear to be no significant differences between the dynamical properties of bulges and ellipticals. Further, the bulges follow a luminosity-central velocity dispersion relation similar to that of elliptical galaxies (Eq. 2.6, Whitmore et al. 1979). It would be interesting to know whether the bulges show a trend between luminosity and rotational properties similar to that for ellipticals, but the present sample does not contain enough bright bulges to test for this. The Sombrero galaxy (NGC 4594) has the most luminous bulge in the sample with MBT = - 20.7, yet it rotates more rapidly than most elliptical galaxies with a similar absolute magnitude.
3 The Holmberg radius is defined as the
radius at which the surface
brightness is 26.5 Bmag/square-arcsec. By Freeeman's law,
rH  4.5
4.5 -1.
Back.
-1.
Back.