


2.3. The luminosity function of galaxies
The galaxy luminosity function
 (L) is defined so
that
(L) is defined so
that  (L)dL
is the number of galaxies per unit volume with luminosities between L
and L + dL.
Schechter (1976)
has found a convenient analytic approximation to the observations,
(L)dL
is the number of galaxies per unit volume with luminosities between L
and L + dL.
Schechter (1976)
has found a convenient analytic approximation to the observations,
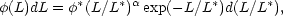 |
(2.18a) |
or, using absolute magnitudes instead of luminosity,
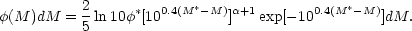 |
(2.18b) |
Using a number of redshift catalogues,
Efstathiou et
al. (1983)
estimate that the best values for the parameters
M*,
 and
and  in Eq. (2.18) are,
in Eq. (2.18) are,
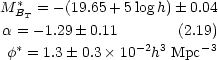 |
(2.19) |
using total magnitudes in the B-band. The normalization of the
luminosity function
 * is
particularly uncertain because of possible
systematic errors. In catalogues of nearby galaxies
* is
particularly uncertain because of possible
systematic errors. In catalogues of nearby galaxies
 * is biased
towards high values because most of the galaxies are located in the
Local Supercluster which is overdense. by. a factor of ~ 2 relative to
the mean luminosity density of the Universe
(Felten, 1977;
Davis et al. 1978).
The normalization can be fixed using deeper surveys, but
there are possible problems with magnitude systems. The magnitudes of
distant galaxies are affected by the red shift of the frequency
distribution of the emitted light (k-corrections) and redshift
surveys of distant galaxies are still quite small.
* is biased
towards high values because most of the galaxies are located in the
Local Supercluster which is overdense. by. a factor of ~ 2 relative to
the mean luminosity density of the Universe
(Felten, 1977;
Davis et al. 1978).
The normalization can be fixed using deeper surveys, but
there are possible problems with magnitude systems. The magnitudes of
distant galaxies are affected by the red shift of the frequency
distribution of the emitted light (k-corrections) and redshift
surveys of distant galaxies are still quite small.
From Eq. (2.18a), the mean space density of galaxies is,
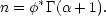 |
(2.20) |
Clearly Eqs. (2.18) and (2.19) cannot hold for arbitrarily small
luminosities since if
 < - 1 Eq. (2.20)
diverges. The shape of the luminosity function at the faint end
(L < 0.005L*) is very uncertain
because although Eq. (2.20) predicts that faint galaxies should be
very abundant in space they are rare in a magnitude-limited catalogue
(see e.g.
Felten, 1977).
< - 1 Eq. (2.20)
diverges. The shape of the luminosity function at the faint end
(L < 0.005L*) is very uncertain
because although Eq. (2.20) predicts that faint galaxies should be
very abundant in space they are rare in a magnitude-limited catalogue
(see e.g.
Felten, 1977).
From Eq. (2.18), the mean luminosity density in the Universe is,
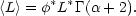 |
(2.21) |
So although the number density of galaxies diverges if
 < - 1, the
mean luminosity density diverges only if
< - 1, the
mean luminosity density diverges only if
 < - 2. Using the numbers
from Eq. (2.19) we find,
< - 2. Using the numbers
from Eq. (2.19) we find,
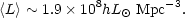 |
(2.22) |
If the mean density of matter in the Universe exceeds the critical value,
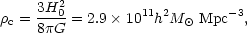 |
(2.23) |
then the Universe is closed (Weinberg, 1972, Ch. 15). Thus Eqs. (2.22) and (2.23) define a mean mass-to-light ratio for an Einstein-de Sitter universe,
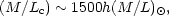 |
(2.24) |
Now we have seen from Sections 2.1 and
2.2 that the typical
mass-to-light ratios of the inner parts of galaxies are
~ 14h(M/L) .
If this were the only material in the Universe then Eq. (2.24) implies
a low density Universe with a cosmological density parameter
.
If this were the only material in the Universe then Eq. (2.24) implies
a low density Universe with a cosmological density parameter
 =
(
=
( /
/
 c) ~
0.01. This number should be regarded as a lower limit because
it is possible that most of the matter in the Universe is dark. In
Section 2.2 we mentioned that the rotation
curves of disc galaxies can
be used as a test for dark material in the outer parts of galaxies but
the best evidence for substantial quantities of dark material comes
from the dynamics of groups and clusters of galaxies
(Section 2.4).
c) ~
0.01. This number should be regarded as a lower limit because
it is possible that most of the matter in the Universe is dark. In
Section 2.2 we mentioned that the rotation
curves of disc galaxies can
be used as a test for dark material in the outer parts of galaxies but
the best evidence for substantial quantities of dark material comes
from the dynamics of groups and clusters of galaxies
(Section 2.4).
It is interesting to examine whether the luminosity function is dependent on environment and whether it has the same shape for different morphological types. The two problems are related because the morphologies of galaxies depend on environment. Rich clusters of galaxies contain mostly ellipticals and SO's (Abell, 1965) whereas in a magnitude limited catalogue of a random patch of the sky more than 70% of the galaxies are spirals. Peebles (1971a) and Schechter (1976) have argued that the luminosity functions of rich clusters of galaxies are indistinguishable from that of the general field. The luminosity functions of rich clusters have been studied in considerable detail by Dressler (1978). He finds significant differences between the luminosity functions of different clusters and presents several clusters for which the Schechter function (Eq. 2.18) is a poor approximation. Tammann, Yahil and Sandage (1979) have determined the luminosity function for various morphological types using the Shapley-Ames catalogue. They do not find any great difference between the luminosity functions of E and SO galaxies compared with Sa-Sc galaxies, but the very late type spirals Sd-Irr are generally fainter than early-type galaxies.