9. PARTICLE PHYSICS AND COSMOLOGY

Considerations from particle physics can have a major impact on much of the preceding discussion. In fact, the predictions of the amplitudes of the largest scale structures observed in the Universe, the dipole and quadrupole anisotropies of the cosmic microwave background radiation, may depend sensitively on the most microscopic scales of the ultimate theory of elementary particles. This apparently paradoxical situation is not really so surprising, given that our theory of large-scale structure depends on the specified initial conditions at an epoch when causally connected regions encompassed only a small number of elementary particles.

9.1. Implications of GUTs

A recent development in cosmology has centered on the application of grand unified theories (GUTs) of the strong, weak and electromagnetic interactions to the very early Universe. Indeed, the extreme energies attained as t 0 provide one of the few environments for studying the implications of GUTs. One of the few fundamental numbers needed to characterize the Friedmann cosmological model is the dimensionless entropy per baryon, equal to 2.5 × 10¹⁰(_b h² / 0.01) for photons and three neutrino flavours. Perhaps the most spectacular success of GUTs has been to provide a natural explanation (at least in order of magnitude) for this number in terms of baryon-non-conserving processes that occur in these theories (see Weinberg, 1982, for a recent review). While the entropy-per-comoving-volume remains approximately constant, the baryon number, an excess of particles over antiparticles, which is initially zero, is generated as the symmetry of the grand unified era is broken soon after the Planck time. Since a universal baryon number is generated, any pre-existing isothermal perturbations, which are equivalent to baryon number or specific entropy variations, cannot survive the baryosynthesis era in the standard model. Only adiabatic perturbations should be present to form galaxies, according to this result.

There is at least one noteworthy means of resurrecting isothermal fluctuations. Spatial variations in the expansion rate on scales larger than the horizon during baryosynthesis will give rise to entropy fluctuations (Bond, Kolb and Silk, 1982; Barrow and Turner, 1981). To understand how this arises, consider first the role of the X-bosons, which unify the electromagnetic, weak, and strong interactions, and consequently mediate proton decay. Only because the baryon non-conserving reactions go out of equilibrium as the Universe expands does baryon number build up, X-bosons being destroyed more often than they are created. 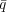Reactions like X qq dominate over X 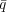by an amount that depends on how much CP violation there is in X-decay. This is a free parameter, although measurements for the kaon system indicate a value ~ 3 × 10^-3 for the fractional amount of CP violation. As the temperature drops to kT << mX ~ 10¹⁵ GeV, both the baryon formation and destruction rates become small relative to the expansion rate, and a net baryon number is frozen out. For a uniformly expanding Friedmann cosmological model, the only free parameter is a value of order 10^-6 is required in order to attain the observed entropy per baryon (Kolb and Wolfram, 1980; Fry, Olive and Turner, 1980).

Now consider the fate of energy density inhomogeneities, which can be decomposed into two independent linear fluctuation modes corresponding to constant and decaying curvature perturbations. While any primordial entropy fluctuations are "cooked" away, the growing mode of primordial adiabatic can in principle perturb the expansion rate at baryosynthesis, except that its effect must be small at this epoch in order to avoid resulting in unacceptably large energy density inhomogeneities in the very early Universe. The decaying curvature mode can lead to a potentially large perturbation of the expansion rate as t 0, provided that the amplitude of the growing mode is initially suppressed. This could happen naturally if one required at, say, the Planck epoch that there was equipartition of energy between the modes (Kompaneets, Lukash and Nvikov, 1982).

There is an additional type of fluctuation that can have a dramatic effect on baryosynthesis, namely spatial variations in the expansion rate due to shear or vorticity perturbations. Shear inhomogeneity includes a decaying mode that could have been large near the Planck time, t_pl ~ (8 Gh_p / c⁵)^1/2 ~ 10^-43 s. One might conjecture that at this epoch, the threshold of cosmology, all possible decaying modes were present, only asymptotically resulting in a nearly uniform Friedmann cosmology. Provided the grand unification era is sufficiently close to the Planek era at kT ~ 10¹⁹ GeV, and supersymmetric unified theories indeed advocate a grand unification energy, mX ~ 10¹⁷ GeV, the decaying modes should still be significant at baryosynthesis. For example, if collisionless particles dominate the energy density, the decaying shear mode = _initial(mX / m_Planck)^1/2 ~ 0.1_initial at this epoch, where is the ratio of shear to expansion rates. Analysis of the effect of shear on baryosynthesis shows that the isothermal fluctuation theory of galaxy formation is still viable if _initial is present on comoving scales well above 10⁶ M. Moreover, the initial shear will have rapidly decayed, and be completely negligible even by the epoch of nucleosynthesis. One can also imagine a universe which initially is dominated by inhomogeneous shear with (m_Planck) >> 1; in this case _B / _B ~ / . One potential source of difficulty in these models is that decaying curvature modes are coupled to growing modes at any transition from a relativistic collisionless to a collisional particle dominated universe (Vishniac, 1982).