6. DISSIPATIONLESS GALAXY FORMATION

6.1. Dissipationless collapse and violent relaxation

Several authors (Sandage, Freeman and Stokes, 1970; Gott and Thuan, 1976) have discussed the possibility that the key process in determining whether a protogalactic cloud becomes an elliptical or spiral galaxy is the amount of binding energy that is dissipated during the collapse of the cloud. In the uniform model of spherical collapse (e.g. Gunn and Gott, 1972), a spherical inhomogeneity reaches its maximum radius r_max at redshift z_m when it achieves an overdensity (z_m) = 9² / 16(z_m).

Hence, it is argued that if star formation is essentially complete at redshift z_m, the subsequent collapse will be purely stellar dynamical and might lead to the formation of spheroidal gas-free systems resembling elliptical galaxies (Gott, 1973, Gott, 1975). On the other hand, if the system is predominantly gaseous at z_m, then the subsequent collapse will be highly dissipative, leading to disc-like systems resembling spiral galaxies. The appeal of the dissipationless model is obvious. It avoids the complexities of gas dynamical calculations and models can, in principle, be studied in detail using N-body simulations.

Using the spherical model, we may make a rough estimate of the redshift at maximum expansion for a typical giant elliptical. At z_m the total energy of the protogalaxy is,

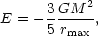(6.1a)

and

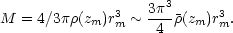(6.1b)

After the collapse and subsequent relaxation of the system, the virial theorem is satisfied, so T = 1/2| W|. We now assume that the density profile is adequately approximated by a de Vaucouleurs r^1/4 profile (Section 2.1) with R_e 6h^-1 kpc. Then W = - 0.33GM² / R_e and the mass of the system may be roughly computed using the virial theorem in the form,

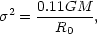(6.2)

where is the average 1-dimensional velocity dispersion, 300 km/sec for a giant elliptical galaxy. Since the collapse is dissipationless, total energy is conserved, so Eqs. (6.1) and (6.2) fix the epoch of galaxy formation (e.g. Binney, 1977).

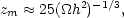(6.3)

Consequently, if ellipticals formed by dissipationless collapse, they must have formed rather early, and with correspondingly short collapse times,

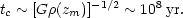(6.4)

One might also expect that the mass-radius (or mass-velocity dispersion) relationship of ellipticals is related to the initial spectrum of fluctuations. Several authors (e.g. Fall, 1980a; Faber, 1982) have used the hierarchical model (Section 5.3) to derive the relation,

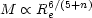(6.5)

where n is the index of the power-law fluctuation spectrum [Eq. (5.9)]. The observations (e.g. Davies et al., 1983) yield M R_e^{1.6 ± 0.3}, hence Eq. (6.5) implies -0.4 < n < - 1.6. This application of Eq. (6.5) is extremely doubtful, however, since the formula ignores the possibility that lumps forming at early times might later agglomerate into larger systems and that there could be a substantial dispersion in the masses of lumps forming at any fixed time. Such a relation could, in principle, be checked using cosmological N-body simulations.

Much of the work on dissipationless galaxy formation has been concerned with predicting the surface brightness profiles of relaxed systems. Elliptical galaxies have remarkably similar density profiles (Section 2.1), an indication of some common relaxation phenomenon. For stellar systems containing only a small number of particles, relaxation may proceed via two-body encounters. Let E be the total energy of any individual star (E = 1/2mv² + ); fluctuations in the gravitational potential result in energy changes E / E ~ 1 on a timescale,

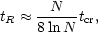(6.6)

where N is the total number of stars in the system and the crossing-time t_cr is defined as t_cr ~ R / v, where v is a characteristic random stellar velocity and R is the half-mass radius of the system. For a giant elliptical galaxy, with N 10¹¹, v 250 km/sec, and R 10 kpc, we obtain t_R 10¹⁶ yrs, i.e. very much longer than the age of the Universe. Thus two-body encounters are entirely negligible in typical galaxies. It is useful to consider the distribution function for the system, f (x, v, t) defined so that the mass density of stars at any given time in a phase space element d³ x d³ v is f (x, v, t) d³x d³v. For a collisionless system, the distribution function f obeys the collisionless Boltzmann equation

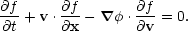(6.7)

Jeans' theorem states that in a collisionless system in a steady-state, the distribution function f will be a function only of the integrals of the equations of motion of any individual star. For example, for an axisymmetric potential there are at least two isolating integrals, the total energy of a star E, and the component of the star's angular momentum around the axis of symmetry J_z. Hence as an ansatz for f we might write f (E, J_z). There exists a wealth of literature on the existence of additional "third-integrals" for given forms of axisymmetric potentials (ie. integrals which are not obviously related to a fundamental symmetry of the Lagrangian). Some aspects of this problem will be discussed below (see the review by Binney, 1982, for a good introduction).

King (1966) showed that elliptical galaxy profiles could be well fitted using the distribution function,

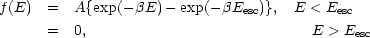(6.8)

where the constants A, , E_esc are treated as free parameters. The distribution function (6.8) is an approximation to the exact steady-state solution of the Fokker-Planck equation ⁽⁷⁾ and the model was designed primarily for non-rotating spherical globular clusters for which two-body relaxation is important (t_R 10⁸ yrs). The good fit to elliptical galaxies was, therefore, somewhat puzzling. Since two-body relaxation is unimportant in giant ellipticals it had been suggested that some sort of mean field relaxation mechanism operating during the collapse phase might be responsible for the distribution function (6.8). The mechanism was first discussed in detail by Lynden-Bell (1967) [see also Shu (1978) for a recent discussion]. Lynden-Bell argued that during the collapse of the galaxy one would expect large fluctuations in the potential / ~ 1. Since the potential is changing, individual stars do not follow energy conserving orbits, hence E / E ~ 1 and the stars undergo a kind of violent relaxation. The subsequent oscillations of the galaxy would be damped within a few collapse times by Landau damping and phase mixing. Lynden-Bell calculated the most probable state to which such violent relaxation would lead, with the result, ⁽⁸⁾

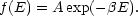(6.9)

This distribution function corresponds to the isothermal sphere (e.g. Chandrasekhar, 1960), which is unacceptable as a model for a galaxy since it leads to a divergent total mass. However, it is clear that high energy orbits with periods longer than the collapse time could not be fully populated. Lynden-Bell argues that such incomplete violent relaxation results in a distribution function of the form (6.8). Since Lynden-Bell's classic paper, a great deal of numerical work has been done to test the theory. Several relevant questions are: (i) Does the theory really lead to density profiles characteristic of elliptical galaxies? (ii) To what extent does the final equilibrium configuration depend on initial conditions such as asphericity? (iii) What happens if the initial state is rotating? We discuss these questions next.

⁷ The Fokker-Planck equation allows an approximate treatment of close-encounters (e.g. Michie, 1963). Back.

⁸ This is the non-degenerate limit of Lynden-Bell's most probable state. Degeneracy effects are unimportant for collisionless systems such as galaxies (Shu, 1978). Back.