6.2. Numerical simulations

In principle, a numerical simulation of the collapse of a protogalaxy offers a good check of violent relaxation. However, in order to avoid problems due to two-body effects using the correct Newtonian potential a large number of particles are required [cf. Eq. (6.6)]. As it is impractical, at present, to use more than ~ 10⁵ particles in an N-body simulation, one has to resort to a softened potential, e.g. (r) = Gm_i m_j / (r_ij² + ²)^1/2. With a suitable choice for the softening parameter , the two-body relaxation time can be made equal to at least a hundred dynamical times for a fairly spherical system. The disadvantage is that a large value of a significantly reduces the resolution of the model. This can be a great limitation, especially if one wants to compare simulations with the inner regions of elliptical galaxies.

Much of the earlier work was done by Gott (1973, 1975) using an axisymmetric potential in order to simplify the force calculation and allow treatment of a relatively large number of "stars" ( 2000). In performing such calculations, one must decide at the outset what might be reasonable initial conditions from which to begin the collapse.

Most workers have decided on simplicity, thus Gott (1973) considers the collapse of uniform spheres of particles with different amounts of solid-body rotation. To some extent these initial conditions may be justified by Crampin and Hoyle's (1964) finding that the distribution of angular momentum per unit mass in spiral galaxies is similar to that of the uniform sphere in solid-body rotation (see also Freeman, 1970, 1975). Gott's (1973) models fail to reproduce the radial density profiles observed in elliptical galaxies, with the numerical models producing (r) r^-4 rather than (r) r^-3. This problem was studied in further detail by Gott (1975) who included the effects of "cosmological infall," in which the protogalaxy accretes material from the expanding cosmological medium. With the addition of cosmological infall Gott managed to obtain good fits to the density and ellipticity profiles of NGC 4697.

Another important result obtained by Gott is the relation between the final ellipticity and the total angular momentum in the case of collapse from spherical initial conditions. The angular momentum of a protogalaxy may be conveniently expressed in terms of the dimensionless parameter

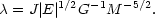(6.10)

Here E is the total energy of the system. Gott's three rotating models were run with values of 0.13, 0.17, 0.21 and achieved final ellipticities, , of approximately 0.15, 0.25, 0.45 respectively. Binney (1978) has used the tensor virial theorem to derive a relationship between the equilibrium ellipticity and the ratio of rotational kinetic energy to the kinetic energy in random motions [cf. Eq. (2.4)]. For oblate spheroids (independent of the radial density profile), the relationship reads,

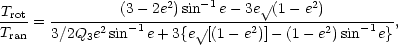(6.11)

where e² = 1 - (1 - )², and Q₃ is a parameter which represents anisotropy the velocity dispersions, Q₃ = -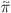₃₃ / (T₁₁ + T₂₂). Here 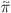_ij is a traceless tensor defined by,

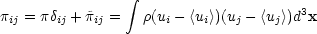(6.12a)

hence 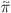_ij represents velocity anisotropy. T_ij is defined as

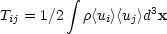(6.12b)

and, we assume that the system rotates about the 3-axis, so that T₁₁ + T₂₂ is just the total kinetic energy of rotation. Gott's models always acquire a final ellipticity that is lower than, predicted by Eq. (6.11) with Q₃ = 0 (isotropic dispersions). Thus for his three models, Eq. (6.11) predicts equilibrium ellipticities of 0.31, 0.46, 0.62 respectively. This result is probably due to velocity anisotropies since the models possess velocity dispersions that are largest perpendicular to the plane (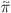₃₃ > 0), a small amount of anisotropy is sufficient to explain the results (Q₃ - 1/3). Gott and Thuan (1976) suggest that the anisotropy is probably an artifact of the coherence of the collapse in the numerical models.

Ostriker and Peebles (1973) conjecture that any stellar-system will be unstable to non-axisymmetric instabilities if the ratio of rotational kinetic energy to potential energy, T_rot / | W| > 0.14. Applying this criterion and Eq. (6.11) we deduce that the maximum flattening of a stable oblate spheroid with isotropic velocity dispersions is 0.42 in agreement with Wilson (1975). The most rapidly rotating of Gott's (1973) models clearly violates the criterion, but since the calculations were constrained to be axisymmetric a bar could not form.

The earliest fully three-dimensional collapse calculation from rapidly rotating initial conditions appears to be the 1000 body model of Dzyuba and Yakubov (1970) in which a uniform sphere in solid body rotation with 0.25 was allowed to collapse. The model was violently bar unstable and settled down to a prolate configuration rotating end over end. Rapidly rotating models with 0.2 have also been run by Miller (1978) and Miller and Smith (1979a, b) using 10⁵ "stars", and in each case the final configuration is approximately prolate and rotating end over end. In an interesting series of experiments, Hohl and Zang (1979) have repeated Gott's (1973) calculations using 10⁴ stars. Models which satisfy the Ostriker-Peebles criterion remain axisymmetric and the results, e.g. the radial density profiles and final ellipticities, agree with those obtained by Gott. However, models run with 0.17 rapidly become bar-like. Hence rapidly rotating ellipticals may be expected to be prolate.

Recently, van Albada (1982) has used a new computational technique to study the collapse and violent relaxation of nearly spherical, though irregular, initial distributions. The most striking result from his study is that models with initially small random motions, T / | W| 0.05 (and, therefore large collapse factors) develop density profiles which are in excellent agreement with de Vaucouleurs' r^1/4 law. Models with large initial random motions, 0.1 T / | W| 0.5, lead to density profiles which are steeper than the r^1/4 law, similar to the results from Gott's (1973) models.

As discussed in Section (2.1) the recent studies of the rotational properties of elliptical galaxies show that most giant ellipticals rotate too slowly for their flattening to be due to rotation. The most likely explanation of these results (Binney, 1978) is that the flattening of ellipticals is due to velocity anisotropy rather than rotation. These observations are inconsistent with the spherical collapse models described above. However, Binney (1976a) and Aarseth and Binney (1978) have shown that acceptable models of flattened ellipticals can be produced by simply relaxing the assumption of spherical initial conditions. These authors have performed 100-500 body numerical simulations starting from non-rotating (or very slowly rotating) highly flattened discs. The models are allowed to violently relax and form flattened equilibrium systems with ellipticities E4-E6 that appear to be good models of elliptical galaxies. Their main results are: (1) The equilibrium configurations have density profiles that may be closely approximated by Hubble's law without any need to invoke the cosmological infall effects required by Gott (1975) in his spherical collapse models. (2) Although rotation is dynamically unimportant in their models, violent relaxation is not efficient enough to sphericalize the system. The equilibrium configurations are generally highly flattened, their flattening being due to velocity anisotropy. Since Aarseth and Binney find that the component of the velocity dispersion in the radial direction _r does not equal the component along the symmetry axis _z, the distribution function cannot be a function of E and J_z alone. Rather the flattening of their model galaxies must be due to a nonclassical third integral of the single particle equations of motion. (3) A model which began from an initially cigar-like configuration relaxed to a triaxial configuration. The model remained triaxial for the entire duration of the run ( 9 crossing times) implying the existence of at least two nonclassical integrals of motion. This latter result is of considerable importance since triaxiality is a natural way in which to explain the isophote twists observed in many elliptical galaxies (Section 2.1). Aarseth and Binney could not be sure that the triaxial form would survive for a Hubble time, but the hypothesis of long-lived triaxial configurations has received additional support from the models of Schwarzschild (1979, 1982) and Wilkinson and James (1982). Although Aarseth and Binney's models seem very promising, it is by no means clear whether their initial conditions are likely to occur in nature. Also, since the median ellipticity of elliptical galaxies is E3 (independent of whether their figures are assumed to be oblate or prolate; Binney, 1978) it would seem that more appropriate initial conditions would be less flattened than those used by Aarseth and Binney. In the next section we address the question of whether it is possible to achieve the required aspherical, initially slowly rotating configurations within the frame-work of the gravitational instability picture.