


7.2.4. The luminosity function of merged objects
An expression for the luminosity function of merged remnants may be derived in a simple way under some restrictive assumptions (Binney and Efstathiou, 1980, unpublished). The number of merged objects NR(m) with mass in the interval (m, m + dm) obeys the equation,
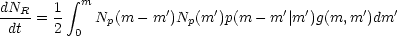 |
(7.5) |
as long as NR(m) << Np(m) for all m. Here Np(m) is the number of progenitors with mass in the interval (m, m + dm), p(m1| m2) is the probability per unit time that galaxies of mass m1 and m2 will merge, g(m1, m2) is the probability that the collision leads to the formation of a galaxy of a different morphological type than the progenitors and is included since it is likely that elliptical type objects would only result from the merging of discs of roughly equal mass. Now the mass dependence of the merger probability function is highly uncertain. In the case of a geometric cross-section, one has
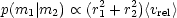 |
(7.6a) |
where r is the half-mass radius and <vrel> is the mean relative velocity, whilst if gravitational focusing is more appropriate, one has
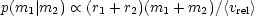 |
(7.6b) |
(Silk and White, 1978).
Hence, assuming a mass-radius relation
r  m
m with 1/2
with 1/2 

 1
(Section 2.1), then (7.6a) and (7.6b) yield
p(m1| m2)
1
(Section 2.1), then (7.6a) and (7.6b) yield
p(m1| m2)
 m1
m1 + m2
+ m2 with 1
with 1 

 2 and we neglect
any mass dependence of
<vrel> which is likely to be small (cf. also
White, 1979a).
Now, the luminosity function of field galaxies is well represented by the
Schechter function (Section 2.3)
2 and we neglect
any mass dependence of
<vrel> which is likely to be small (cf. also
White, 1979a).
Now, the luminosity function of field galaxies is well represented by the
Schechter function (Section 2.3)
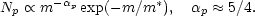 |
(7.7) |
If g(m, m') is a fairly narrow function,
g  1,|
m - m'|
1,|
m - m'|

 m, g
m, g
 0,| m -
m'| >
0,| m -
m'| >
 m, Eq. 7.5 gives
m, Eq. 7.5 gives
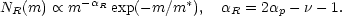 |
(7.8) |
Hence, this simple model predicts that the luminosity function of
merged remnants will be of the Schechter form with identical
characteristic mass m*, as that for the
progenitors. The faint end
slope,  p,
will only be the same if
p,
will only be the same if  =
=
 p - 1
p - 1
 1/4. Clearly if the
merger probability increases strongly with mass, the model predicts a
lack of faint merger remnants when compared with the progenitor mass
function.
1/4. Clearly if the
merger probability increases strongly with mass, the model predicts a
lack of faint merger remnants when compared with the progenitor mass
function.
The non-linear development of NR(m) has been
studied by Binney and
Efstathiou using Monte-Carlo simulations for various forms of
p(m1| m2)
and g(| m1 - m2|).
(10)
The linear solution discussed above is well obeyed at
first. However, at later times when
NR(m*)
 Np(m*)
remnant-progenitor
collisions become important. Indeed, if the mass dependence of the
merger probability is such that
Np(m*)
remnant-progenitor
collisions become important. Indeed, if the mass dependence of the
merger probability is such that

 1, a runaway
growth of large mass
remnants occurs whilst the form of NR(m)
remains essentially
unchanged at the low mass end. This effect has also been noticed by
Ostriker and Hausman
(1977)
and Aarseth and Fall
(1980).
Clearly such
a runaway growth cannot occur if merged remnants are to be identified
with elliptical galaxies. In a realistic case the merger probability
will be significantly reduced in regions of high velocity dispersion
such as the rich clusters of galaxies. This important dynamical effect
is not included in the above calculations.
1, a runaway
growth of large mass
remnants occurs whilst the form of NR(m)
remains essentially
unchanged at the low mass end. This effect has also been noticed by
Ostriker and Hausman
(1977)
and Aarseth and Fall
(1980).
Clearly such
a runaway growth cannot occur if merged remnants are to be identified
with elliptical galaxies. In a realistic case the merger probability
will be significantly reduced in regions of high velocity dispersion
such as the rich clusters of galaxies. This important dynamical effect
is not included in the above calculations.
Despite the uncertainties, it would seem that galaxies formed by mergers should have a different luminosity function than that of the progenitors. Further, if the merger probability increases strongly with mass there should be a deficiency of low mass remnants relative to the progenitors (see also Roos (1981)). As discussed in Section 2.3, observations of the luminosity function of galaxies separated by morphological type do not reveal any large differences between the luminosity functions of ellipticals and spirals. Rich compact clusters, which are dominated by early type galaxies, generally have luminosity functions similar to the field luminosity function. There is, of course, considerable scope for improvement of both the theory and observations before this can be used as an argument for or against the merger hypothesis.
10 A similar study has been made by Roos (1981) using a somewhat different scheme. Back.