9.2. Massive neutrinos

Another far-reaching implication of GUTs is that neutrinos should possess a non-zero rest mass. While the GUTs only indicate a minimal lower bound (m > 10^-6 eV), there are tentative (and presently unconfined) experimental indications that m could be as large as 30 eV from a tritium decay experiment (Lyubimov et al., 1980). The early results from a neutrino oscillation experiment (Reiner, Sobel and Pasiern, 1980) have not been confirmed; since this type of experiment measures a mass difference and a mixing angle, a null result is still consistent with a finite neutrino mass. These preliminary results have motivated cosmologists to reconsider the implications of a neutrino rest mass. The mass density of cosmological background neutrinos exceeds the luminous matter density if the neutrino rest mass m (assumed to be in one flavour) 1 eV, and closes the Universe if m > 100h² eV. A neutrino mass in the range 10-30 eV also has a dramatic effect on galaxy formation theory (cf. Section 5.2).

With primordial adiabatic fluctuations, there are associated fluctuations in the neutrino density. Secondary neutrino fluctuations are also generated by isothermal or stress perturbations once they cross the horizon in the matter-dominated era. Neutrino perturbations undergo collisionless damping on sub-horizon scales; this defines a characteristic comoving mass-scale M_m 4 × 10¹⁵ m₃₀^-2 M, to which corresponds a comoving length-scale = 40m₃₀^-1 Mpc, where m₃₀ is the neutrino mass (in one flavour) in 30 eV units. This is analogous to the Jeans length in a collisional fluid, except that density fluctuations cannot be sustained at all on smaller scales while growing via gravitational instability on larger scales. In dimensionless units, M_m m_pl³ m^-2, where m_pl is the Planck mass.

Two effects are responsible for the damping. While the neutrinos are relativistic, phase mixing occurs between peaks and troughs of adjacent waves. When the neutrinos are non-relativistic, the fluctuations disperse by Landau damping, the faster neutrinos overtaking the slower neutrinos. In either case, the neutrino velocity dispersion v_s determines the effective Jeans length. While the neutrinos are relativistic, the instantaneous neutrino Jeans length ~ v_s t increases as t, and when the neutrinos become non-relativistic, v_s a^-1 and t^1/3 . Consequently, the Jeans mass ^{3 3} t^-2 attains a peak value M_m at redshift 1 + z_m = 35, 000m₃₀ (Bond, Efstathiou and Silk, 1980; Doroshkevich et al., 1980b). The neutrinos actually become non-relativistic at a somewhat larger redshift 57,300 m₃₀. No primordial neutrino fluctuations can be sustained on scales below M_m although primordial entropy fluctuations (as defined in Section 4.2) do generate secondary adiabatic fluctuations on scales above but below M_m. This occurs because of the associated stress perturbation induced since p / c² for an isothermal fluctuation, whereas p = /3 is the background equation of state at early epochs. This results in the generation of energy density fluctuations once the appropriate wave-length first enters the horizon. This effect is only significant once the predominant constituent of the Universe is non-relativistic. In principle, one could fine-tune the initial conditions to remove this secondary adiabatic component by subtracting a small adiabatic fluctuation from the primordial entropy perturbation, but this may require a very specific choice of initial conditions.

Damping of neutrino fluctuations is extremely severe on scales below . Detailed computations of the damping of fluctuations in a neutrino universe involve a simultaneous solution of the Boltzmann transport equation for the collisionless neutrinos and the perturbed Einstein equations for the evolution of density perturbations (Peebles, 1982a; Bond and Szalay, 1983). The neutrinos are still semirelativistic when much of the damping occurs, and the system of equations must be evaluated numerically. Computations of the evolution of several Fourier components of the density fluctuation spectrum show that a wave with = 1/3 suffers extreme damping by a factor ~ 200 before its growth phase begins after the neutrino velocity dispersion has dropped sufficiently, whereas one with = 2 suffers very little damping. The damping of a given component is first effective when about one-half wavelength of the Fourier component has entered the horizon, for .

The baryonic component of adiabatic fluctuations also suffers damping from radiative viscosity and diffusion on scales below M_d ~ 3 × 10¹³ _b^{-1/2 -3/4} h^-5/2 ~ 10¹⁵ M, coincidentally within an order of magnitude of the baryonic mass associated with M_m, namely M_bm ~ 1.2 × 10¹⁴ m₃₀^-3 h² M. Baryonic fluctuations on scales above M_d and below the baryonic Jeans mass (~ 10¹⁷ just prior to decoupling) do not grow significantly in amplitude until after the decoupling epoch.

In the Newtonian limit, valid for sub-horizon fluctuations and for non-relativistic particles, the growth of baryonic density fluctuations is determined by

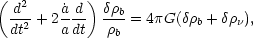where _b and are the spatial Fourier transforms of the perturbed baryon and neutrino densities. Inspection of the solutions to this equation reveals three regimes for post-decoupling evolution of baryonic fluctuations. On scales > , the baryonic fluctuations, even if zero initially, respond rapidly to any preexisting neutrino fluctuations. On scales < but above the neutrino Jeans mass at decoupling, preexisting neutrino fluctuations have been erased. However, baryonic fluctuations may be present which can drive secondary neutrino fluctuations. The baryonic component only grows freely after decoupling, when one finally has a baryon fluctuation spectrum inhibited in amplitude by a factor _b / . Finally on scales below the neutrino Jeans mass at decoupling, all growth is suppressed until the relevant scale eventually above the instantaneous value of the neutrino Jeans mass, which decreases as the Universe expands adiabatically. The results from the linear theory of fluctuation growth are schematically summarized in Figure 9.1.

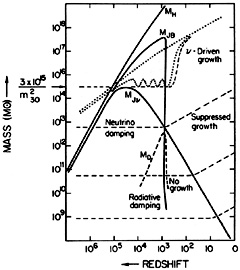Figure 9.1. Fluctuation growth in a neutrino-dominated universe. Dotted lines indicate schematic evolution with redshift of adiabatic density fluctuations and broken lines the evolution of isothermal fluctuations for different mass scales that correspond to the scale on the ordinate. Heavy lines show the characteristic mass scales: MH is the horizon mass, MJB is the baryonic Jeans mass, MJ is the neutrino Jeans mass (assuming m = 30 eV), and MD is the baryonic damping mass. (From Silk (1982)).

With adiabatic initial conditions, the first fluctuations to become nonlinear have masses of order M_m, and these undergo aspherical collapse preferentially along one axis, as envisaged in the original Zel'dovich pancake theory. Because of the sharp cut-off of structure at short wavelengths, a caustic surface forms as trajectories intersect. The baryonic component develops a radiative shock, and undergoes fragmentation as described in Section 8.3. The neutrinos freely penetrate the caustics and separate from the baryon. Multiple streaming motions develop in the midplane, due to the infalling high velocity neutrinos while neutrinos initially near the midplane retain Low velocities. It is likely that such a configuration is unstable in the presence of the inhomogeneous baryonic component, the gravitational two-stream and Jeans instabilities being effective as the streams interpenetrate. The baryonic fragments perturb the local gravitational potential in such a way as to generate sheet-like density fluctuations. A similar phenomenon appears to be present in N-body collapses of spheroidal distributions of particles (Miller and Smith, 1979). According to one-dimensional N-body simulations of the pancake collapse, streaming progressively develops in phase space as neutrinos that have already passed through the plane are turned back, seeing a deeper gravitational well as the infall continues. One ends up with a sandwich of bound neutrinos surrounding a fragmented baryonic pancake.

According to one-dimensional simulations (Doroshkevich et al., 1980b; Melott, 1982; Bond, Szalay and White, 1983), a substantial fraction of the neutrinos retain a low velocity until several collapse times (in a direction perpendicular to the plane of symmetry) have elapsed and these cold neutrinos become bound to the baryonic fragments. Little dilution of phase space density occurs for these neutrinos. A similar effect is well known from earlier studies of one-dimensional collapse (e.g. Janin, 1971). One expects that the mass fraction of neutrinos should increase progressively with the depth of the potential well of the baryonic core. Consequently, neutrino infall can at least qualitatively account for the dark matter in galaxy halos if the neutrino mass is 30 eV (Tremaine and Gunn, 1979) and also produce an increase in mass-to-luminosity ratio with increasing scale.

Massive neutrinos may, perhaps, rescue the adiabatic fluctuation model from two otherwise nearly fatal difficulties. Since most of the power in the density fluctuation spectrum is at a mass-scale M_m as opposed to being spread over the range between the damping mass and the baryonic Jeans mass prior to decoupling, the correlation function is greatly reduced at large scales if m ~ 30 eV. The observations may be consistent with a primordial adiabatic density fluctuation power spectrum / kⁿ with either n = 0 (white noise) or n = 1, the constant curvature value that offers such theoretical appeal (but see White, Frenk and Davis, 1983). Because the neutrino fluctuations grow between z_nr and decoupling, whereas the radiation fluctuations do not, the strong coupling after the recombination epoch between radiation, baryons and neutrinos results in radiation temperature fluctuations that are reduced by a factor ~ z_d / z_nr. This applies on small and intermediate angular scales, and suffices to reconcile the observational upper limits with the anisotropy required to form galaxies in the adiabatic model. The large angular-scale anisotropy presents more of a problem, since here the gravitational potential fluctuations are relatively independent of m and cause large-scale structure in the microwave background radiation. Because the power in fluctuations on the horizon scale prior to decoupling is reduced, however, neutrinos do improve matters. The removal of the broad peak in the matter fluctuation spectrum suppresses the dipole anisotropy (to which it contributes an appreciable amount) more strongly than the quadrupole anisotropy, which is largely due to potential fluctuations on our present horizon scale associated with scales >> M_m. Any desired amount of quadrupole anisotropy can now be accounted for without producing excessive dipole anisotropy if n 0 (Figure 4.3). It should be emphasized, however, that the most recent results have failed to confirm previous indications of quadrupole anisotropy (Fixsen, Cheng and Wilkinson, 1983; Lubin, Epstein and Smoot, 1983).