


4.2.3. Central Velocity Dispersions. II. Mass-to-Light Ratios
Since elliptical galaxies contain little material in nearly circular
orbits, their masses are usually calculated using central velocity
dispersions and the virial theorem. A review of such mass determinations
is given in
Faber and Gallagher
(1979).
However, total masses
can be calculated only by assuming that the mass-to-light ratio
M/L is
the same everywhere in the galaxy, and that the velocity distribution
is everywhere isotropic with constant
 . These assumptions are
probably not correct. Therefore, only core mass-to-light ratios will
be discussed in this section. Their determination requires fewer and
better-justified assumptions
(King and Minkowski
1972;
Faber and Gallagher
1979),
although not ones which are observationally verified.
If the velocity distribution is strongly anisotropic near the center,
then even these masses will be greatly in error
(Binney and Mamon 1982;
Tremaine and Ostriker
1982;
see since 3.3.8).
. These assumptions are
probably not correct. Therefore, only core mass-to-light ratios will
be discussed in this section. Their determination requires fewer and
better-justified assumptions
(King and Minkowski
1972;
Faber and Gallagher
1979),
although not ones which are observationally verified.
If the velocity distribution is strongly anisotropic near the center,
then even these masses will be greatly in error
(Binney and Mamon 1982;
Tremaine and Ostriker
1982;
see since 3.3.8).
If we assume that cores are isothermal, then the virial theorem gives central mass-to-light ratios
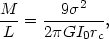 |
(21) |
where I0 is the central surface brightness (King 1966; Schechter 1980). Conveniently, the combination I0rc is relatively insensitive to seeing. At present M/L values can be calculated for only a few galaxies because there is not enough published photometry. For 17 giant ellipticals, Schechter (1980) finds an average value of <M/LB> = 7.8 (dispersion = 3.2) in solar units. (Here I have corrected the values for NGC 4552 and 4636 for photometric zero-point errors in King 1978; see Boroson and Kormendy 1982). The only disk-galaxy bulge for which there exists sufficient photometry is M31; Faber and Gallagher (1979) obtain M/LB = 8.5. If we briefly relax our adopted restriction and consider global M/L determinations, then there exist slightly more data. Faber and Gallagher (1979) obtain <M/LB> = 7.8 ± 1.3 for five additional (S0) bulges. The data are very sparse but there seems to be considerable homogeneity in these stellar populations.
One question of considerable interest is the possible dependence
of M/L on L. With data on only a score of galaxies, a plot of
M/L versus L
(Schechter 1980,
Fig.2) has so much scatter that any weak
luminosity dependence is masked. However, we can look for a luminosity
dependence using mean relations between core parameters.
Faber and Jackson
(1976)
combined the L 
 4 relation
with other power-law
relations (not explicitly stated) between I0,
rc and L to derive
M/L
4 relation
with other power-law
relations (not explicitly stated) between I0,
rc and L to derive
M/L  L0.5. On the other hand, S2BS assumed that
all galaxies have
the same surface brightness, in which case the relation
L
L0.5. On the other hand, S2BS assumed that
all galaxies have
the same surface brightness, in which case the relation
L 
 4 and the
virial theorem
M
4 and the
virial theorem
M 
 2
rc imply that
M/L
2
rc imply that
M/L  L0. Other determinations
include M/L
L0. Other determinations
include M/L  L1/8
(Schechter and Gunn
1978)
and M/L
L1/8
(Schechter and Gunn
1978)
and M/L  L0.34
(Michard 1980,
for global mass-to-light ratios).
L0.34
(Michard 1980,
for global mass-to-light ratios).
The mean parameter correlations derived in this paper allow a new
determination of the luminosity dependence of M/L. The required
relations are (1)
L 
 5.4 from
section 4.2.2, (2)
5.4 from
section 4.2.2, (2)

 rc0.25 from Figure 22,
(3) a similar relation
I0
rc0.25 from Figure 22,
(3) a similar relation
I0  rc-0.87, not illustrated
but derived in the same way as (2), and (4) the virial theorem,
M/L
rc-0.87, not illustrated
but derived in the same way as (2), and (4) the virial theorem,
M/L 
 2 /
I0rc.
Combining these gives
2 /
I0rc.
Combining these gives
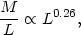 |
(22) |
intermediate between the results of
Faber and Jackson
(1976)
and of S2BS and
Schechter (1980).
Note that if we assume that
L 
 4, then
the above relation becomes
M/L
4, then
the above relation becomes
M/L  L0.49, in agreement with Faber and Jackson.
L0.49, in agreement with Faber and Jackson.
The above weak dependence of M/L on L is consistent
with
Tinsley's (1978)
population models of elliptical galaxies. These model the
observed color-magnitude relations by varying the metallicity (cf.
Michard 1980).
Tinsley predicts that
M/L  L0.13, which is certainly
consistent with equation (22) in view of the small sample of data.
This is a reassuring indication. However, there is a clear need for
data on more than ~ 20 galaxies, with a greater range of luminosity
than is represented in current measurements.
L0.13, which is certainly
consistent with equation (22) in view of the small sample of data.
This is a reassuring indication. However, there is a clear need for
data on more than ~ 20 galaxies, with a greater range of luminosity
than is represented in current measurements.