


When clusters of galaxies were found to be an important class of X-ray sources, there were a number of suggestions as to the primary X-ray emission mechanism. The three most prominent ideas were that the emission resulted from thermal bremsstrahlung from a hot diffuse intracluster gas (Felten et al., 1966), or that the emission resulted from inverse Compton scattering of cosmic background photons up to X-ray energies by relativistic electrons within the cluster (Brecher and Burbidge, 1972; Bridle and Feldman, 1972; Costain et al., 1972; Perola and Reinhardt, 1972; Harris and Romanishin, 1974; Rephaeli, 1977a, b), or that the emission was due to a population of individual stellar X-ray sources, like those found in our galaxy (Katz, 1976; Fabian et al., 1976). Subsequent observations have provided a great deal of support for the thermal bremsstrahlung model, and have generally not supported the other two suggestions. These three emission mechanisms will be briefly reviewed, and a few of the arguments in favor of thermal bremsstrahlung and against the other two models will be cited.
5.1.1. Inverse Compton emission
As noted in Section 3.2, many X-ray
clusters also have strong radio emission, and
cluster radio emission is distinguished by having a large spectral index
 r. This
led to the idea that the X-ray emission might be produced by the same
relativistic electrons that produce the synchrotron radio emission. Very
high energy electrons, with very short lifetimes, would be required to
produce the emission by synchrotron emission, but much lower energy
electrons could scatter low energy background photons up to X-ray energies
(Felten and Morrison,
1966).
If the electrons are extremely relativistic,
with energies Ee =
r. This
led to the idea that the X-ray emission might be produced by the same
relativistic electrons that produce the synchrotron radio emission. Very
high energy electrons, with very short lifetimes, would be required to
produce the emission by synchrotron emission, but much lower energy
electrons could scatter low energy background photons up to X-ray energies
(Felten and Morrison,
1966).
If the electrons are extremely relativistic,
with energies Ee =
 me c2 for
me c2 for
 >>
1, and the initial frequency of the background photon is
>>
1, and the initial frequency of the background photon is
 b, then on average
the frequency after the scattering will be
b, then on average
the frequency after the scattering will be
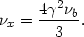
| (5.1) |
Because the cluster radio spectra vary as power-laws, it is generally assumed that the relativistic electrons have a power-law energy distribution
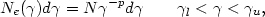
| (5.2) |
where Ned
 is the
number of electrons with energies between
is the
number of electrons with energies between
 and
and
 +
d
+
d .
Then, the resulting inverse Compton (IC) radiation has a spectrum given
by
.
Then, the resulting inverse Compton (IC) radiation has a spectrum given
by
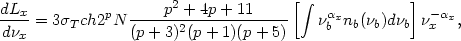
| (5.3) |
where Lx is the X-ray luminosity, nb
is the number density of background photons as a function of frequency
 b,
b,
 T is the
Thomson cross section, and the X-ray spectral index is
T is the
Thomson cross section, and the X-ray spectral index is
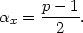
| (5.4) |
A source of low energy photons that is present everywhere and dominates the overall photon density in the universe is the 3 K cosmic background radiation. If the background is taken to be a blackbody radiation field at a temperature Tr, then
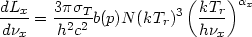
| (5.5) |
for frequencies in the range
 l2 << (h
l2 << (h
 x /
kTr) <<
x /
kTr) <<
 u2. Here
u2. Here
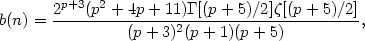
| (5.6) |
and  and
and
 are the
gamma and Riemann zeta functions.
are the
gamma and Riemann zeta functions.
Now, the synchrotron radio luminosity Lr produced by the same electron population is given by
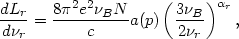
| (5.7) |
where  B
B
 (eB/
2
(eB/
2 mec) is
the gyrofrequency in the magnetic field B, and
mec) is
the gyrofrequency in the magnetic field B, and
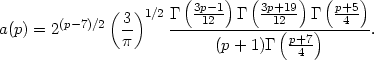
| (5.8) |
Equation (5.8) assumes that the electron distribution is isotropic and
that the frequency is in the range
 l2 <<
(
l2 <<
( r /
r /
 B) <<
B) <<
 u2. The radio spectral index
u2. The radio spectral index
 r is
equal to the X-ray spectral index
r is
equal to the X-ray spectral index
 x.
x.
Thus the synchrotron radio and IC X-ray emission from the same relativistic electrons will have the same spectral shape, and the luminosities in the two spectral regimes are also very simply related:

| (5.9) |
where Ur and UB =
(B2 /
8 ) are the energy densities of
the background
radiation and the magnetic field, respectively. Because fluxes
(fx, fr) at single
frequencies are easier to measure than integrated luminosities, it is
useful to note that (in cgs units)
) are the energy densities of
the background
radiation and the magnetic field, respectively. Because fluxes
(fx, fr) at single
frequencies are easier to measure than integrated luminosities, it is
useful to note that (in cgs units)
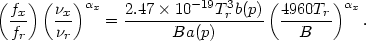
| (5.10) |
Since the temperature of the cosmic background radiation is known, the ratio
of radio and IC X-ray fluxes determines the magnetic field strength
(Harris and Romanishin,
1974).
If the X-ray emission from clusters were due to inverse
Compton emission, the magnetic field would typically be B
 0.1
µG. Fields at least ten times larger than this are expected
if the relativistic electrons and
the magnetic field have equal energy densities; the small magnetic fields
required by the IC model would increase the energy requirements for
cluster radio sources by about two orders of magnitude. On the other
hand, if the X-rays are not due to IC emission, than this value is a lower
limit to the magnetic field strength in the radio emitting region
(Section 4.3.1).
0.1
µG. Fields at least ten times larger than this are expected
if the relativistic electrons and
the magnetic field have equal energy densities; the small magnetic fields
required by the IC model would increase the energy requirements for
cluster radio sources by about two orders of magnitude. On the other
hand, if the X-rays are not due to IC emission, than this value is a lower
limit to the magnetic field strength in the radio emitting region
(Section 4.3.1).
For a magnetic field of B
 1 µG,
radio photons at a frequency of 1 GHz are produced by electrons with
1 µG,
radio photons at a frequency of 1 GHz are produced by electrons with

 2 ×
104. Similarly, IC X-ray emission at a photon
energy of 1 keV is produced by electrons with
2 ×
104. Similarly, IC X-ray emission at a photon
energy of 1 keV is produced by electrons with

 103. Thus
the electrons that
could produce the observed X-ray emission would produce very low frequency
radio emission, typically at a frequency of 20 MHz if B
103. Thus
the electrons that
could produce the observed X-ray emission would produce very low frequency
radio emission, typically at a frequency of 20 MHz if B
 1 µG, and
at an even lower frequency if B is lower as required in this
model. Such low frequency radio
emission generally cannot be detected from the Earth. However, one
argument in
favor of the IC model of cluster X-ray emission was that cluster radio
sources have steep spectra (Section 3.1),
indicating that they have many
lower energy relativistic electrons, as required to explain their X-ray
emission.
1 µG, and
at an even lower frequency if B is lower as required in this
model. Such low frequency radio
emission generally cannot be detected from the Earth. However, one
argument in
favor of the IC model of cluster X-ray emission was that cluster radio
sources have steep spectra (Section 3.1),
indicating that they have many
lower energy relativistic electrons, as required to explain their X-ray
emission.
There is now considerable evidence against the IC model. In this model, one would expect a very strong correlation between the low frequency radio flux and the X-ray flux (equation 5.10). The reality of any radio-X-ray correlation is questionable (Section 3.2), and recent larger samples of X-ray clusters from HEAO-1 and Einstein do not support such a strong correlation. In the IC model, the radio and X-ray emission would come from identical spatial regions and would therefore have identical distributions on the sky. However, while the X-ray emission is extended and diffuse (Section 4.4), the radio emission comes primarily from individual radio galaxies. Only a very small fraction of clusters appear to have significant diffuse radio halo emission (Section 3.4). The IC model predicts that clusters have power-law X-ray spectra, which is not consistent with the best X-ray spectral observations (Section 2.3.1); one clear distinction is that a power-law provides much more high energy X-ray emission than an exponential thermal spectrum (Section 5.1.3), and such emission is either not seen or very weak. The IC model would not produce any of the X-ray line emission that is seen universally in clusters that have been observed with reasonable sensitivity (Sections 4.3.2 and 4.3.3). The magnetic field is required to be much weaker than would be favored by radio observations. The distorted radio morphologies in clusters would not be explained in this model. Finally, most of the X-ray - optical correlations could not be accounted for naturally in the IC model.