5.4.4. Viscosity

If there are shears in the velocity in a fluid, then viscosity will produce forces that act against these shears. A unit volume of the fluid will be subjected to a force given by

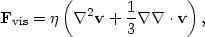
(5.45)

where is the dynamic viscosity, and the bulk viscosity has been assumed to be zero. For an ionized plasma without a magnetic field, is given by

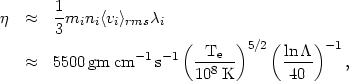
(5.46)

where m_i, n_i, <v_i>_rms, and _i are the mass, number density, rms velocity, and mean free path of ions, respectively. Like the thermal conductivity, the dynamic viscosity is independent of density and depends strongly on the temperature. However, because of the dependence on the particle mass, the viscosity is primarily due to ions, not electrons. The Reynolds number for flow at a speed v past an object of size l is defined as Re _g vl / , which can be written as

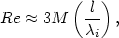
(5.47)

where M v/c_s is the Mach number and c_s is the sound speed. As noted in Section 5.3.4, this indicates that the flow around moving galaxies in a cluster is probably laminar, but not certainly so. The viscosity affects the rate of heating of the intracluster gas by galaxy motions (Section 5.3.4), and the rate of stripping by interstellar gas in cluster galaxies (Section 5.9).

As with thermal conduction, one can define a velocity scale length l_v so that the absolute value of the term in parentheses in equation (5.45) is <v_i>_rms / l_v². Then, if the ion mean free path _i is shorter than l_v, equation (5.45) applies. However, if l_v < _i, then equation (5.45) requires that the viscous stresses exceed the ion pressure and that momentum be transported faster than the thermal speed of the ions. This is not possible, and the viscous stresses must saturate at a value comparable to the ion pressure. To my knowledge, this effect has not been included in calculations of astrophysical fluid flows. It should be particularly important in flows around galaxies, where previous calculations, particularly those involving Kelvin-Helmholtz instabilities, have applied equation (5.45) to flows with very large shears.