


5.9. Stripping of gas from galaxies in clusters
The galaxies found in rich clusters generally have considerably less gas than galaxies in the field (Section 2.10.2). Their 21 cm radio line luminosities indicate that they have less neutral gas than more isolated galaxies (see Section 3.7 and the many references therein), and they also appear to have weaker optical line fluxes from ionized gas (Gisler, 1978). The galaxies in rich, regular, X-ray luminous clusters are predominantly ellipticals and S0s (Sections 2.5 and 2.10.1, Table 1), and the spirals that are seen in clusters often have weak ('anemic') spiral arms (van den Bergh, 1976) and tend to be found at large projected distances from the cluster center (Gregory, 1975; Melnick and Sargent, 1977). The fraction of spiral galaxies is anticorrelated with the X-ray luminosity of the cluster (Bahcall, 1977c; Melnick and Sargent, 1977; Tytler and Vidal, 1979; Figure 30; equation 4.9) and with the local galaxy density (Dressler, 1980b). A primary difference between spiral galaxies and ellipticals or S0s is that spirals contains large amounts of gas.
These observations suggest that gas in galaxies in clusters may be removed by some process. In Section 2.10.2 the possibility that the differences in the galaxian populations of clusters and the field might result from the stripping of gas from spiral galaxies was discussed. This hypothesis is very controversial, and it appears unlikely that spiral stripping alone accounts for all the differences between different types of galaxies. Nonetheless, even within individual galaxy classes (Hubble types), galaxies in clusters appear to have less gas (Sullivan et al., 1981; Giovanardi et al., 1983; Section 3.7). This suggests that some process must remove gas from galaxies in clusters, even if this stripping does not solely determine the morphology of galaxies.
In addition to this indirect evidence for gas removal, the X-ray observations of M86 suggest that it is currently being stripped of gas (Forman et al., 1979; Fabian et al., 1980; Sections 4.5.3 and 5.8.3). There are also a number of cases where optical or 21 cm radio observations may show gas currently being stripped from galaxies (see, for example, Gallagher, 1978).
Mathews and Baker (1971) showed that, once an isolated elliptical or S0 galaxy had been stripped of its gas, supernova driven winds would keep it gas free. If the interstellar gas density is low, then the energy input from supernovae cannot be radiated away, and heats the gas until it flows out of the galaxy (Sections 5.3.3 and 5.6). If the galaxy is immersed in intracluster gas, this mechanism is less effective, since the wind must overcome the confining pressure of the intracluster gas.
Spitzer and Baade (1951) suggested that collisions between spiral galaxies in the cores of compact clusters remove the interstellar medium from the disks of these galaxies. Their basic argument was that the stellar components of galaxies could pass through one another, because two-body gravitational interaction between galaxies or their component stars is very ineffective (Section 2.9.1). However, the mean free paths of gas atoms or ions (Section 5.4.1) are relatively short, and in the center of mass frame for the collision, the kinetic energy of the gas will be thermalized. If the gas cannot cool rapidly, it will be heated to a temperature at which it is no longer bound to either galaxy, since galaxies within a cluster move much more rapidly than stars move within galaxies. If the gas cools rapidly, it will still be left at rest in the center of mass frame, while the galaxies move away from it. In either case, the gas is no longer bound to either galaxy, since it has more kinetic energy (either thermal or bulk) than the maximum galaxy binding energy.
Spitzer and Baade estimated the rate of gas removal in the Coma cluster assuming all the galaxies were equivalent, and that the galaxies all had radial orbits, and found that a galaxy should be stripped in less than 108 yr. This is probably an underestimate of the time scale, since galaxy orbits are probably not radial, and a typical off-center collision between two galaxies of dissimilar mass and density may not remove all of the gas from both galaxies. Moreover, subsequent increases in the extragalactic distance scale have had the effect of increasing the time scale for this process. Sarazin (1979) estimated the mean time scale for collisional stripping of galaxies in a cluster, averaging over the cluster velocity dispersion, the spatial distribution of galaxies, and the diameters and masses of galaxies, and found a rate about 100 times smaller.
Gunn and Gott (1972)
suggested that galaxies lose their interstellar gas by
ram pressure ablation because of the rapid motion of the galaxies
through the
intracluster gas. They were primarily concerned with stripping gaseous disks
from spiral galaxies to make S0s. Based on a static force balance
argument, they
suggested that a gaseous disk would be removed when the ram pressure
Pr =
 g
v2 exceeded the restoring gravitational force per unit
area in the disk
2
g
v2 exceeded the restoring gravitational force per unit
area in the disk
2 G
G  D
D
 ISM (where
ISM (where
 g
is the intracluster gas density, v is the galaxy velocity,
g
is the intracluster gas density, v is the galaxy velocity,
 D
the surface density of the spiral disk, and
D
the surface density of the spiral disk, and
 ISM the
surface density of
interstellar gas in the disk). Taking v2 =
3
ISM the
surface density of
interstellar gas in the disk). Taking v2 =
3 r2
for a typical galaxy in a cluster with a line-of-sight velocity dispersion
r2
for a typical galaxy in a cluster with a line-of-sight velocity dispersion
 r, and
assuming the disk has a uniform surface density, with a radius
rD and mass MD, this condition
becomes
r, and
assuming the disk has a uniform surface density, with a radius
rD and mass MD, this condition
becomes
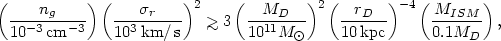
| (5.114) |
where ng is the number density of atoms in the intracluster medium and MISM is the mass of interstellar medium in the disk.
Tarter (1975) and Kritsuk (1983) have given a simple semianalytical treatment of the stripping of gas disks in spiral galaxies in clusters by integrating the net force due to ram pressure and gravity, assuming one-dimensional motion. For a given intracluster gas distribution, they found the smallest distance from the cluster center at which a galaxy could retain its gas. The calculations by Tarter indicated that most spirals should be stripped fairly easily in X-ray clusters, and that remaining spirals would only be found in the outer parts. On the other hand, Kritsuk suggested that molecular clouds might be very difficult to strip from spirals.
It is interesting to calculate the expected dependence of the spiral
fraction and the typical distance of spirals from the cluster center on
the cluster X-ray luminosity, if one assumes that all clusters originally
had the same spiral-rich galactic populations at all positions. If one also
assumes that the reduction in the fraction of spirals is due to ram pressure
ablation, that a spiral is stripped whenever the ram pressure exceeds a
critical amount (given by equation 5.114 or something similar), that the
galaxies in clusters have an analytic King isothermal distribution (equation
5.57), and that the gas is isothermal and hydrostatic (equation 5.63),
then the spiral fraction varies as fSp
 A- B
log Lx, where Lx is the
X-ray luminosity and A and B are constants. This is just
the empirical relationship found by
Bahcall (1977c)
(equation 4.9; Figure 30). The
radius of a typical spiral varies as rSp /
rc
A- B
log Lx, where Lx is the
X-ray luminosity and A and B are constants. This is just
the empirical relationship found by
Bahcall (1977c)
(equation 4.9; Figure 30). The
radius of a typical spiral varies as rSp /
rc
 (Lx)1/6
(Lx)1/6 , where rc is the
core radius and
, where rc is the
core radius and
 is the ratio
of gas and galaxy temperatures (equation 5.64).
is the ratio
of gas and galaxy temperatures (equation 5.64).
The majority of galaxies presently in X-ray clusters are ellipticals and S0s
that have a more spherical stellar distribution.
Sarazin (1979) gave a
semi-analytic treatment of the stripping of gas from spherical galaxies,
using basically the same formulation as
Tarter (1975).
He found that
galaxies would be stripped if the ram pressure were greater than about
2GMgal
 ISM
/ R2, where mgal and r are
the galaxy mass and radius, respectively.
Takeda et al.
(1984)
performed numerical hydrodynamic
simulations and derived a critical ram pressure of
2
ISM
/ R2, where mgal and r are
the galaxy mass and radius, respectively.
Takeda et al.
(1984)
performed numerical hydrodynamic
simulations and derived a critical ram pressure of
2 ISM
ISM
 *2. Assuming
that the ram pressure is much greater than this limit, the time scale for
ram pressure stripping of a galaxy, defined as trp
*2. Assuming
that the ram pressure is much greater than this limit, the time scale for
ram pressure stripping of a galaxy, defined as trp
 (d ln mISM / dt)-1, is
(d ln mISM / dt)-1, is
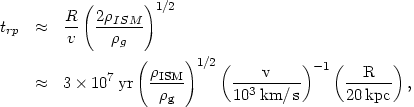
| (5.115) |
where
 ISM
is the average interstellar gas density,
ISM
is the average interstellar gas density,
 g
is the intracluster gas
density, v and Mgal are the galaxy velocity and
mass, respectively. The
calculations of Tarter and Sarazin assume that there are no sources of
gas in the galaxy.
g
is the intracluster gas
density, v and Mgal are the galaxy velocity and
mass, respectively. The
calculations of Tarter and Sarazin assume that there are no sources of
gas in the galaxy.
Gisler (1976,
1979)
pointed out that it would be more difficult to strip a
galaxy if the stars in the galaxy were constantly resupplying it with
gas. Then,
the ram pressure must overcome the momentum flux due to this mass input, as
well as the gravitational attraction of the galaxy. He derived an
approximate analytical relationship for the ram pressure needed to strip
gas out of a galaxy
out to a projected radius b, ignoring pressure forces in the gas
and assuming
one-dimensional motion. If the rate of gas loss by stars in the galaxy is
 ISM =
ISM =
 *
*
 * where
* where
 * is the mass density of stars in the
galaxy, then he
found that gas would be stripped at any projected radius b such that
the ram pressure exceeded
* is the mass density of stars in the
galaxy, then he
found that gas would be stripped at any projected radius b such that
the ram pressure exceeded
 8
8 *
*
 *(b)
*(b)
 *.
Here,
*.
Here,
 *(b)
is the projected stellar mass density at b, and
*(b)
is the projected stellar mass density at b, and
 * is
the line-of-sight velocity dispersion of
stars in the galaxy. For a typical giant elliptical galaxy in a typical
X-ray
cluster, Gisler found that all the gas is lost if the rate of input is
less than
0.1 M
* is
the line-of-sight velocity dispersion of
stars in the galaxy. For a typical giant elliptical galaxy in a typical
X-ray
cluster, Gisler found that all the gas is lost if the rate of input is
less than
0.1 M /
yr, and that all the gas is retained if it is greater than about 3
M
/
yr, and that all the gas is retained if it is greater than about 3
M /
yr. For intermediate values, a core of interstellar gas is retained by
the galaxy.
/
yr. For intermediate values, a core of interstellar gas is retained by
the galaxy.
Gisler's treatment ignored pressure forces, which must be important in elliptical galaxies (Jones and Owen, 1979; Takeda et al., 1984). Jones and Owen argued that extended gas in elliptical galaxies must be hot (the sound speed in the gas must be comparable to the velocity dispersion of stars), and that pressure forces in the gas cannot be ignored. A pressure gradient may be set up in the interstellar gas that opposes the ram pressure; they argued that this increases the region of a galaxy that is shielded from stripping by about a factor of ten over Gisler's result. Then elliptical galaxies will typically retain cores of interstellar gas with radii of about 10 kpc, and Jones and Owen argue that this gas can explain the existence of well-defined radio jets in the inner parts of head-tail radio sources (Section 3.3; Figure 9).
Takeda et al. (1984) recently rederived Gisler's condition for continuous stripping of gas from galaxies with stellar gas loss, including pressure forces. They find that the correct condition for stripping is that the ram pressure exceed
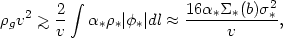
| (5.116) |
where  *
is the galaxy gravitational potential. Equation (5.116) differs from
Gisler's result by a factor of
*
is the galaxy gravitational potential. Equation (5.116) differs from
Gisler's result by a factor of
 2
2 *
/ v.
*
/ v.
Most of these calculations of stripping have been based on semianalytic estimates, which assume the motion to be one-dimensional, generally ignore the finite temperature and compressibility of the gases, and ignore any viscous forces. To avoid these assumptions and test the efficiency of ram pressure ablation, a large number of numerical hydrodynamic simulations have been made by , Lea and De Young (1976), Toyama and Ikeuchi (1980), and Nepveu (1981a). These studies have all taken the galaxy to be spherical, and the simulations have been two-dimensional, with the flows assumed to be axially symmetric. Lea and De Young started with a galaxy with a significant amount of interstellar gas, moving in the midst of intracluster gas. On the other hand, Gisler was mainly interested in the effects of stellar mass loss on ram pressure ablation, and he started with an empty galaxy. The numerical calculations indicate that stripping occurs even more easily than the simple analytic force balance arguments suggest. Unless the rate of mass input due to stars is high, a typical galaxy will be stripped almost completely during a single passage through the core of a cluster if the intracluster gas density exceeds roughly 10-4 atom / cm3.
Recently, Shaviv and Salpeter (1982) and Gaetz et al. (1985) made two-dimensional hydrodynamic calculations of ram pressure ablation for galaxies with stellar mass loss, including the cooling of the gas. Gaetz et al. also included star formation. They found that gas was ablated from the outer portions of the galaxy, but was retained in the inner portions and formed a cooling flow. One very useful feature of Gaetz et al. is that the hydro simulations were used to derive analytic fitting formulas for many physical quantities associated with the gas flows.
All of these numerical calculations start with the galaxy in the middle of a uniform cluster. Recently, Takeda et al. (1984) calculated the stripping of gas from a galaxy moving on a radial orbit from the outer parts of the cluster into the core. Stellar mass loss was assumed to add to the interstellar gas in the galaxy. The stripping was determined from two-dimensional hydrodynamic simulations. After the first passage through the cluster core, the behavior was periodic, with the galaxy accumulating interstellar gas when far from the core and losing nearly all of it when it passed through the core on each orbit. A large fraction of the accumulated interstellar gas was pushed out in a single 'blob' on each passage through the cluster core. These calculations may provide a model for the galaxy M86, other gas containing galaxies, and the galaxyless extended X-ray sources in A1367 (Sections 4.5.3, 4.5.4 and 5.8.3). The latter might be blobs released from stripped galaxies (Takeda et al., 1984).
Under many circumstances, transport processes such as viscosity and turbulent mixing can be more important than ram pressure in removing gas from a galaxy in a cluster (Livio et al., 1980; Nepveu, 1981b; Nulsen, 1982). Nulsen has calculated the rate of laminar viscous stripping and stripping due to turbulence, and finds a viscous stripping time scale
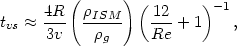
| (5.117) |
where Re is the Reynolds number (equation 5.47). In many cases, this is faster than the rate of ram pressure ablation given by equation (5.115). However, one caution is that the viscous stresses may saturate, since the mean free paths of ions are similar to the sizes of galaxies (Section 5.4.4).
Livio et al.
(1980)
suggest that the Kelvin-Helmholtz instability at the
boundary between interstellar and intracluster gas can produce 'spikes' of
interstellar gas protruding into the intracluster gas, which are sheared
off, increasing the stripping rate. They estimate a mass loss rate roughly
 KH
KH

 ISM
ISM
 R2
R2
 KH
/ tKH, where
KH
/ tKH, where
 KH
KH
 1021 cm
and tKH
1021 cm
and tKH
 106 yr are the
wavelength and growth time of the fastest growing modes. This stripping
rate is
considerably smaller than that given by equation (5.117). Moreover,
Nulsen (1982)
has argued that Livio et al. overestimated this rate because they
ignored
the effect of compressibility on the instability, and because they did
not include
the effect of the mass loss on the instability. Another problem is that the
wavelength of the fastest growing mode is shorter than the ion mean
free path
106 yr are the
wavelength and growth time of the fastest growing modes. This stripping
rate is
considerably smaller than that given by equation (5.117). Moreover,
Nulsen (1982)
has argued that Livio et al. overestimated this rate because they
ignored
the effect of compressibility on the instability, and because they did
not include
the effect of the mass loss on the instability. Another problem is that the
wavelength of the fastest growing mode is shorter than the ion mean
free path  KH
<<
KH
<<  i,
and the viscosity expression used is therefore not
valid (Section 5.4.4).
Nulsen showed that the instability was suppressed
when viscosity is significant, and that the mass loss is not controlled by
the fastest growing modes but by the induced velocities on the largest
scales.
i,
and the viscosity expression used is therefore not
valid (Section 5.4.4).
Nulsen showed that the instability was suppressed
when viscosity is significant, and that the mass loss is not controlled by
the fastest growing modes but by the induced velocities on the largest
scales.
Another mechanism for removing gas from galaxies, which can operate even when the galaxies are moving slowly through the intracluster gas, is evaporation (Gunn and Gott, 1972; Cowie and McKee, 1977; Cowie and Songaila, 1977). Heat is conducted into the cooler galactic gas from the hotter intracluster gas, and if the rate of heat conduction exceeds the cooling rate, the galactic gas will heat up and evaporate. If cooling is assumed to be small, the evaporation rate with unsaturated conduction for a spherical galaxy immersed in intracluster gas of temperature Tg is (Cowie and Songaila, 1977)
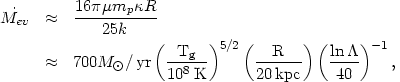
| (5.118) |
where  is the thermal
conductivity (Section 5.4.2;
equation 5.37) and
is the thermal
conductivity (Section 5.4.2;
equation 5.37) and  is the
Coulomb logarithm (equation 5.33). The stripping rate is a factor of
(2/
is the
Coulomb logarithm (equation 5.33). The stripping rate is a factor of
(2/ ) smaller for a disk galaxy
with the same radius. The evaporation
rate will be significantly reduced if the conductivity saturates
(Section 5.4.2),
as is probably the case at least for disk galaxies. Unfortunately,
thermal conductivity also depends critically on the magnetic field geometry
(Section 5.4.3).
If the conductivity is not suppressed by the magnetic
field, this mechanism can play an important role in stripping gas from
galaxies.
) smaller for a disk galaxy
with the same radius. The evaporation
rate will be significantly reduced if the conductivity saturates
(Section 5.4.2),
as is probably the case at least for disk galaxies. Unfortunately,
thermal conductivity also depends critically on the magnetic field geometry
(Section 5.4.3).
If the conductivity is not suppressed by the magnetic
field, this mechanism can play an important role in stripping gas from
galaxies.
As pointed out by Nulsen (1982), there is a simple connection between mass loss by evaporation and mass loss by laminar viscosity (the Re term in equation 5.117). At low velocities, this term dominates, and the viscous stripping rate is nearly independent of velocity, because the Reynolds number is proportional to velocity. Since both thermal conduction and ionic viscosity are transport processes and the ion and electron mean free paths are essentially equal, the rates of stripping from these two processes are simply related:
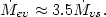
| (5.119) |
While this expression was derived for unsaturated conduction and viscosity and no magnetic suppression of either, it probably will remain approximately true even when these effects are included, since both thermal conduction and viscosity are affected similarly.