


5.4.3. Effects of the magnetic field
Charged particles gyrate around magnetic field lines on orbits with a
radius (the gyroradius) of rg =
(mv c/ZeB), where m is the particle mass,
v
c/ZeB), where m is the particle mass,
v is the
component of its velocity perpendicular to the magnetic field, z
is the particle charge, and B is the magnetic field strength. If
v
is the
component of its velocity perpendicular to the magnetic field, z
is the particle charge, and B is the magnetic field strength. If
v =
(2 k Tg / m)1/2, which is the rms
value in a thermal plasma, then
=
(2 k Tg / m)1/2, which is the rms
value in a thermal plasma, then
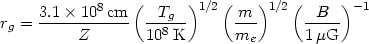
| (5.44) |
which is much smaller then any length scale of interest in clusters, and
is also much smaller than the mean free path of particles due to collisions
rg <<
 e.
Then, the effective mean free path for diffusion perpendicular to the
magnetic field is only on the order of rg2
/
e.
Then, the effective mean free path for diffusion perpendicular to the
magnetic field is only on the order of rg2
/  e
(Spitzer, 1956).
Because they have larger
gyroradii, the ions are most effective in transport processes
perpendicular to the magnetic field. In practice, the gyroradii are so
small that diffusion perpendicular to the magnetic field can be ignored
in the intracluster gas.
e
(Spitzer, 1956).
Because they have larger
gyroradii, the ions are most effective in transport processes
perpendicular to the magnetic field. In practice, the gyroradii are so
small that diffusion perpendicular to the magnetic field can be ignored
in the intracluster gas.
Consider the effect of the magnetic field on thermal conduction, when the
temperature gradient lies at an angle
 to the local magnetic
field direction. Only the component of the gradient parallel to the
field is effective in driving a heat
flux, and only the the component of the resulting heat flux in the
direction of the temperature gradient transports any net energy. If the
conduction is unsaturated,
the heat flux parallel to the thermal gradient is thus reduced by a
factor of
cos 2
to the local magnetic
field direction. Only the component of the gradient parallel to the
field is effective in driving a heat
flux, and only the the component of the resulting heat flux in the
direction of the temperature gradient transports any net energy. If the
conduction is unsaturated,
the heat flux parallel to the thermal gradient is thus reduced by a
factor of
cos 2 .
If the conduction is saturated, the heat flux is independent of the
temperature gradient; the appropriate factor is just
cos
.
If the conduction is saturated, the heat flux is independent of the
temperature gradient; the appropriate factor is just
cos  (Cowie and McKee,
1977).
(Cowie and McKee,
1977).
Observations suggest that the magnetic field in clusters may be tangled, so
that the direction  varies throughout the intracluster gas
(Section 3.6).
Let lB be the coherence length of the magnetic
field, so that the field will typically have changed direction by
varies throughout the intracluster gas
(Section 3.6).
Let lB be the coherence length of the magnetic
field, so that the field will typically have changed direction by
 90° over this
distance. Let
lT be the temperature scale height
(Section 5.4.2 above) and let
90° over this
distance. Let
lT be the temperature scale height
(Section 5.4.2 above) and let
 e be
the mean free path of electrons. Consider first the case where
e be
the mean free path of electrons. Consider first the case where
 e
<< lT,
so that the conduction is unsaturated. Then, if
lB
e
<< lT,
so that the conduction is unsaturated. Then, if
lB  lT, the magnetic
field is ordered over the scales of interest in the cluster, and the value
of cos 2
lT, the magnetic
field is ordered over the scales of interest in the cluster, and the value
of cos 2 depends on the geometry of the magnetic field. For example,
for a cluster with a radial temperature gradient and a circumferential
magnetic field, thermal conduction would be suppressed. Alternatively,
if lT >> lB >>
depends on the geometry of the magnetic field. For example,
for a cluster with a radial temperature gradient and a circumferential
magnetic field, thermal conduction would be suppressed. Alternatively,
if lT >> lB >>
 e, then the
field direction can be treated as a random
variable, and the heat flux is reduced by
e, then the
field direction can be treated as a random
variable, and the heat flux is reduced by
 <
cos2
<
cos2  >
= 1 / 3. If the coherence
length of the magnetic field is less than the mean free path
lB <<
>
= 1 / 3. If the coherence
length of the magnetic field is less than the mean free path
lB <<
 e, the
conductivity depends on the topology of the magnetic field (i.e.,
whether it is connected over distances greater than
lB). In general, the effective mean
free path for diffusion will always be at least as small as
lB, and could
be as small as lB2
/
e, the
conductivity depends on the topology of the magnetic field (i.e.,
whether it is connected over distances greater than
lB). In general, the effective mean
free path for diffusion will always be at least as small as
lB, and could
be as small as lB2
/  e if the
magnetic field is disconnected on the scale
of lB. In this limit, the thermal conduction would be
very significantly reduced.
e if the
magnetic field is disconnected on the scale
of lB. In this limit, the thermal conduction would be
very significantly reduced.
The Faraday rotation observations
(Section 3.6) suggest
that lB

 e
e
 20
kpc. Thus thermal conduction will probably be reduced by a factor of at
least 1/3, and the conductivity time scale (equations 5.41 and 5.43)
should be increased by at least this factor.
20
kpc. Thus thermal conduction will probably be reduced by a factor of at
least 1/3, and the conductivity time scale (equations 5.41 and 5.43)
should be increased by at least this factor.