


5.5.6. Chemically inhomogeneous equilibrium models
The heavier an ion is, the slower its thermal motion in the intracluster gas will be. As a result, heavy ions will tend to drift toward the center of the cluster. In Section 5.4.5 the drift rate was calculated and shown to be rather slow, although the precise value depends on cluster parameters. Further, the intracluster magnetic field may be very effective in retarding any sedimentation of heavy elements. Nonetheless, it is possible that heavier elements may have drifted to the cluster center in some cases, or been introduced into the intracluster gas quite near the center. Eventually, the motion of heavy ions towards the cluster center will stop when the resulting charge separation produces an electric field that cancels the effect of the gravitational field.
Abramopoulos et al. (1981) have calculated chemically inhomogeneous models for the intracluster gas in thermodynamic equilibrium. The temperature of the gas is therefore constant, both spatially and among the various ions and electrons. These models satisfy the hydrostatic equation (5.55) for the total pressure, but this does not uniquely define the chemically inhomogeneous model, since any value of the total pressure can be attributed to an infinite number of different combinations of partial pressures of different ions. In thermodynamic equilibrium, the number density of any ion is given by the Boltzmann equation
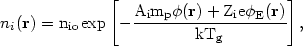
| (5.86) |
where Ai, zi, and
nio are the mass, charge, and central density
of the ion i. The cluster gravitational potential
 and electrical potential
and electrical potential
 e are defined in
this equation to be zero at the cluster center. The gravitational
potential is assumed to be fixed and known, as in most of the
hydrostatic models discussed in the previous sections. The electrical
potential is given as a solution of Poisson's equation
e are defined in
this equation to be zero at the cluster center. The gravitational
potential is assumed to be fixed and known, as in most of the
hydrostatic models discussed in the previous sections. The electrical
potential is given as a solution of Poisson's equation
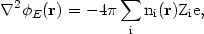
| (5.87) |
where the sum includes electrons as one of the ionic species. Because the
coupling constant for electrical forces exceeds that of gravitational
forces by
 1040,
while the fraction of the cluster mass due to intracluster gas is much
greater than the inverse of this, the electrical potential will generally be
quite small
1040,
while the fraction of the cluster mass due to intracluster gas is much
greater than the inverse of this, the electrical potential will generally be
quite small
 E
E
 -
- mp /
e, and a sufficient approximation to the solution
of equation (5.87) is to assume that the gas is very nearly electrically
neutral:
mp /
e, and a sufficient approximation to the solution
of equation (5.87) is to assume that the gas is very nearly electrically
neutral:
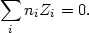
| (5.88) |
The electric potential is then given by requiring a simultaneous solution of
equations (5.86) and (5.88), and requiring that the total abundance
 ni
dV of each of the ions be fixed.
ni
dV of each of the ions be fixed.
In the case where the plasma can be assumed to consist only of protons and
electrons, with the abundances of all heavy elements being so low that
they do not contribute to the potential, the solution for the ion and
electron densities is
the same as the isothermal hydrostatic solution given above (equation
5.63), the electric potential is
 e =
-mp
e =
-mp
 / 2e, and the
densities of any trace heavy elements will be
/ 2e, and the
densities of any trace heavy elements will be
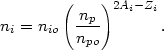
| (5.89) |
Unfortunately, the abundance of helium certainly can not be treated as
insignificant, and other heavier elements may contribute to the electric
potential near the cluster core. Equations (5.86) and (5.88) have been
solved numerically
by Abramopoulos et
al. (1981),
assuming an analytic King potential for the cluster, taking the gas
temperature to be
 = 2/3
(equation 5.64), and assuming
a range of heavy element abundances from pure hydrogen and helium to solar.
They find that the heavy elements are strongly concentrated to the
cluster core. To balance the resulting increase in the charge density,
the electrons also must be centrally condensed.
= 2/3
(equation 5.64), and assuming
a range of heavy element abundances from pure hydrogen and helium to solar.
They find that the heavy elements are strongly concentrated to the
cluster core. To balance the resulting increase in the charge density,
the electrons also must be centrally condensed.
The concentration of heavy elements to the cluster core, where the electron density is high, results in an increase in the X-ray line intensity for a given set of heavy element abundances. As a result, Abramopoulos et al. (1981) argue that the observed line strengths could be produced by gas with iron abundances of only 1/20 of solar.