


5.6. Wind models for the intracluster gas
If the rate of heating of the intracluster medium is sufficiently large,
the gas will
be heated to the escape temperature from the cluster, and will form a wind
leaving the cluster. Since the sound crossing time across a cluster is
relatively
short (equation 5.54), the cluster would be emptied of gas rapidly
unless gas were constantly being added to the cluster.
Yahil and Ostriker
(1973)
suggested that gas is being injected into the intracluster medium at
rates of 103 - 104
M / yr,
and is sufficiently heated to produce a steady-state
outflow of gas. These mass ejection rates are considerably larger than those
expected from stellar mass loss from visible stars in galaxies
(Section 5.10).
/ yr,
and is sufficiently heated to produce a steady-state
outflow of gas. These mass ejection rates are considerably larger than those
expected from stellar mass loss from visible stars in galaxies
(Section 5.10).
Let  be
the rate of mass input per unit volume into the intracluster gas, and
let h(r) be the heating rate per unit volume. If the
cluster is assumed to be spherically symmetric, with a gravitational
potential
be
the rate of mass input per unit volume into the intracluster gas, and
let h(r) be the heating rate per unit volume. If the
cluster is assumed to be spherically symmetric, with a gravitational
potential
 (r), and the gas is
injected
into the cluster with no net velocity, but with the velocity dispersion of
the galaxies, then the hydrodynamic equations for a steady-state wind
are
(r), and the gas is
injected
into the cluster with no net velocity, but with the velocity dispersion of
the galaxies, then the hydrodynamic equations for a steady-state wind
are

|

| (5.90) |

|
where
 g,
P, and v are, respectively, the gas density, pressure,
and velocity,
and
g,
P, and v are, respectively, the gas density, pressure,
and velocity,
and  r is the
one-dimensional velocity dispersion of the galaxies in the cluster.
r is the
one-dimensional velocity dispersion of the galaxies in the cluster.
Yahil and Ostriker argued that the source of mass input into the cluster was mass loss by stars in cluster galaxies, and that

| (5.91) |
where  is the
total mass density of the cluster and
is the
total mass density of the cluster and
 *-1 is the characteristic
time scale for gas ejection from galaxies. They argued that
*-1 is the characteristic
time scale for gas ejection from galaxies. They argued that
 *-1
*-1
 1012 yr.
1012 yr.
Yahil and Ostriker considered two mechanisms that might heat the gas.
First, if the gas were ejected by supernovae it could be heated within
galaxies before being ejected into the cluster
(Section 5.3.3; equation 5.27);
they referred to this as the HIG (heating in galaxies) model. Defining

 3kTej
/ (2µmp
3kTej
/ (2µmp
 r2),
the heating rate due to ejection from galaxies becomes
r2),
the heating rate due to ejection from galaxies becomes

| (5.92) |
Alternatively, Yahil and Ostriker suggested that the heating might be due to the motion of galaxies through the cluster (Section 5.3.4); they referred to this as the HBF (heating by friction) model. Then, the heating rate is

| (5.93) |
where RD is the drag radius (equation 5.28),
mgal 
 /
ngal is the total cluster mass per galaxy,
/
ngal is the total cluster mass per galaxy,
 v is the
velocity of the galaxy relative to the gas (which is
moving at v), and the average is over the Gaussian distribution
of galaxy velocities. It is useful to define
v is the
velocity of the galaxy relative to the gas (which is
moving at v), and the average is over the Gaussian distribution
of galaxy velocities. It is useful to define
 (r)
such that h(r)
(r)
such that h(r)

 (r)
(r)
 r2
r2
 , so
that
, so
that  is
constant in the HIG model, and
is
constant in the HIG model, and
 (r)
(r)

 RD2
RD2
 g
g
 r
/
r
/  *
mgal in the HBF model.
*
mgal in the HBF model.
Let the cluster density be given by
 =
=  0
g(x), where
0
g(x), where
 0 is
the central density,
x
0 is
the central density,
x  r/rc, rc is the cluster core radius,
and g(x) is a dimensionless function.
Similarly, let the cluster potential be written as
r/rc, rc is the cluster core radius,
and g(x) is a dimensionless function.
Similarly, let the cluster potential be written as
 (r) =
(r) =
 0
0
 (x), where
(x), where
 0 is the
central potential. If the mass distribution is assumed to be isothermal,
so that
0 is the
central potential. If the mass distribution is assumed to be isothermal,
so that  r
is constant and is related to the cluster central potential
r
is constant and is related to the cluster central potential
 0 and the central
density
0 and the central
density
 0
by equations (5.60) and (5.61), then the equation of continuity becomes
0
by equations (5.60) and (5.61), then the equation of continuity becomes

| (5.94) |

|
If the King analytic form of the cluster density is assumed, then
g, G, and
 are
given by the functions on the right-hand sides of equations (5.57), (5.58)
and (5.59), respectively. The energy equation can also be integrated to
give
are
given by the functions on the right-hand sides of equations (5.57), (5.58)
and (5.59), respectively. The energy equation can also be integrated to
give

| (5.95) |
where  and
and
 are the integrated
heating rate and potential energy
are the integrated
heating rate and potential energy

| (5.96) |

|
The left-hand side of equation (5.95) is positive definite, which implies that there is a minimum heating rate at any radius
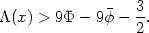
| (5.97) |
If the King analytic model for the potential is assumed, then the maximum
value for the right-hand side of equation (5.97) is 1.35, and this is
the minimum
value of  in the HIG
model (equation 5.92). Similarly, the central temperature is given by
in the HIG
model (equation 5.92). Similarly, the central temperature is given by

| (5.98) |
so that the minimum central temperature in the HIG model is

| (5.99) |
Similar arguments for the HBF model indicate that
 RD2
RD2
 go
go
 r
/(
r
/( *
mgal)
*
mgal)
 3/2,
and that the central temperature is
3/2,
and that the central temperature is

| (5.100) |
These analytic results were given in Bahcall and Sarazin (1978). The temperatures are lower than those in a href="Sarazin_refs.html#869" target="ads_dw">Yahil and Ostriker (1973) because they assumed µ = 1, which is not valid for an ionized plasma.
The observed cluster temperatures (Section 4.3.1) are generally below those required by equations (5.99) or (5.100), so it does not seem that the gas is heated sufficiently to produce a wind. The energy required to support such a wind also seems to be prohibitively large, since it would require that considerably more than the whole thermal content of the gas (more because of the kinetic energy of the flow) be produced in a flow time, which for a transonic wind is comparable to a sound crossing time. In the HIG model, this would require a very large supernova rate or other energy source; in the HBF model, it would require that the galaxies have delivered to the gas much more kinetic energy than they currently possess (Section 5.3.4). As a result, it seems unlikely that wind models fit the distribution of the intracluster gas at all radii, but it remains possible that gas is flowing out from the outer portions of clusters.
a href="Sarazin_refs.html#473" target="ads_dw">Livio et al. (1978) argue that viscous drag between intracluster and interstellar gas can produce a very large heating rate due to galaxy motions if the intracluster gas is sufficiently hot, so that the Reynolds number is small (equations 5.46 and 5.47). As discussed in Section 5.3.4, this requires that galaxies maintain large amounts of intracluster gas; it seems more likely that the drag forces will strip the gas from the galaxies. Unless the galaxies have a large rate of mass outflow, Rephaeli and Salpeter (1980) have shown that the drag does not increase for small Reynolds number (Section 5.4.4). Again, there is the problem that the heating required to support a strong wind is greater than the total kinetic energy content of the galaxies.
Lea and Holman (1978)
discussed winds driven by heating by relativistic
electrons (Section 5.3.5).
They derived analytic heating limits like those of
equation (5.59). To produce a steady-state wind, the heating rate must
be much
greater than that necessary to heat the gas in a Hubble time, and as a
result the required values of
 l
are very low. They find that even in the Perseus cluster,
which is one of the strongest radio clusters known,
l
are very low. They find that even in the Perseus cluster,
which is one of the strongest radio clusters known,
 l
<< (B / µG)-(
l
<< (B / µG)-( r+1)/2
r+1)/2 r is
required for a steady-state wind. Moreover, this mechanism suffers the
problem that extended halo radio sources, of the sort necessary to heat
the intracluster gas, are relatively rare.
r is
required for a steady-state wind. Moreover, this mechanism suffers the
problem that extended halo radio sources, of the sort necessary to heat
the intracluster gas, are relatively rare.
In summary, it seems unlikely that the intracluster gas in most clusters is involved in steady-state outflow, although gas may be flowing out of the outer portions of clusters.