5.5.5. Total masses and mass distributions in clusters-the hydrostatic method

Masses for individual galaxies or for clusters of galaxies can be derived from the distribution of their X-ray emitting gas if this gas is in hydrostatic equilibrium. This is a reasonable approximation as long as the cluster is stationary (the gravitational potential does not change on a sound crossing time), forces other than gas pressure and gravity (magnetic fields, for example) are not important, and any motions in the gas are subsonic. Estimates of intracluster magnetic fields based on radio observations (Chapter 4) show that they are much too small to have a significant dynamical effect. In Section 5.6, we will show that supersonic expansion of the gas (cluster winds) is unlikely. Some clusters show evidence for a slow settling of the intracluster gas due to cooling at the cluster center (a cooling flow; Sections 4.3, 4.4, and 5.7), but these motions are very subsonic except possibly very near the cluster center (r 1 kpc; equation 5.105).

Under these circumstances, the gas obeys the hydrostatic equation (5.56), and the cluster mass m(r) can be determined if the density and temperature of the intracluster gas are known. This method of determining the mass has a number of advantages over the use of the virial theorem (Section 2.8) or any other method which uses the galaxies as test particles. First, the gas is a collisional fluid, and the particle velocities are isotropically distributed. On the other hand, galaxies in clusters (or stars in galaxies) are collisionless, and uncertainties in the velocity anisotropy can significantly affect mass determinations. Second, the hydrostatic method gives the mass as a function of radius, rather than the total mass alone as given by the virial method. Third, the statistical accuracy of this method is not limited by the number of galaxies in the cluster; the statistical accuracy can be improved by lengthening the observation time. Fourth, better statistics in the X-ray measurements means that it is easier to avoid problems with background contamination, and to resolve possible uncertainities due to subclustering (Geller and Beers, 1982). Finally, hydrostatic mass determinations are not very sensitive to the shape of the cluster (Strimpel and Binney, 1979; Fabricant et al., 1984).

The first applications of this method to determine mass distributions were by Bahcall and Sarazin (1977) and Mathews (1978). The method has been developed extensively by Fabricant et al. (1980, 1984) and Fabricant and Gorenstein (1983). Applications of the method have been reviewed by Sarazin (1986b). Ideally, one would measure the spatially and spectrally resolved X-ray surface brightness I(b) to directly deconvolve the gas density and temperature as a function of the radius (Section 5.5.4; equations 5.80 through 5.83). The mass is then given by the hydrostatic equation, which can be written as

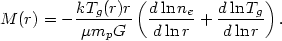
Note that the mass depends only weakly on the gas density n_e (only its logarithmic derivative enters), but depends strongly on the gas temperature.

Unfortunately, as discussed in Section 5.5.4, the limited spectral response of the Einstein X-ray observatory has prevented the direct determination of temperature profiles for the intracluster gas. Accurate profiles of the gas density are known. In order to apply the hydrostatic method to clusters, some simple assumption must be made about the temperature distribution T_g(r). Unfortunately, because the mass is strongly affected by T_g, this means that the resulting mass profiles will be very uncertain. Several analyses (Vallee, 1981; Fabricant et al., 1984) have assumed that gas is isothermal (Section 5.5.1) or that the gas temperature and density are related by a simple polytropic equation (Section 5.5.2). These analyses give a somewhat smaller total cluster mass than previous virial estimates, and as noted in Section 5.5.1, somewhat higher gas masses.

As discussed in Section 4.3, excellent global cluster X-ray spectra exist from the HEAO-1 A-2 detectors. These spectra generally cannot be fit by emission at a single temperature (Henriksen, 1985). The spectra can be used to determine the amount of gas (or, more precisely, the amount of EI = n_p n_eV, where Vis the volume (equation 4.3)) as a function of temperature, but cannot tell us where the gas is located because of their poor spatial resolution. The Einstein imaging observations give n_e(r) (which can be integrated to give n_p n_eV), but give no information about the temperature structure. However, the comparison of these two results ((EI vs. T_g) and (EI vs. r)) allow the determination of (T_g vs. r), if we assume that T_g is a monotonic function of the radius r (Henriksen, 1985; Henriksen and Mushotzky, 1986; Cowie et al., 1987). Since the observed gas densities vary at large distances like an isothermal sphere _g r^-2 (equation 5.73), while these mass determinations require that the gas temperature decrease with radius, the total mass density will always decrease with radius more rapidly than the gas density. Since the total density is the sum of the gas density, the galaxy density, and the missing mass density, these determinations suggest that the missing mass is concentrated towards the cluster center. For the Coma cluster, this method gives a missing mass density which is more centrally concentrated than that of the galaxies, which is in turn more centrally concentrated than that of the intracluster gas. Values of the mass-to-light ratio of the entire cluster of M/L_V 100h₅₀ are found, with the intracluster gas contributing about 30% of the mass.

If these monotonic temperature mass determinations are correct, one is lead to a different picture of the missing mass than that presented in Section 2.8. If the missing mass is more concentrated than the visible matter in the cluster, it suggests that the missing mass has undergone dissipation. Combined with the smaller ratio of missing mass to visible mass, this suggests that the missing mass is baryonic matter, and not some weakly interacting species. The major uncertainty in these analyses is the assumption of a monotonic temperature gradient. While this seems quite plausible, there is no compelling physical argument requiring that this be true. While most detailed models for the ejection or infall of intracluster gas give monotonic gradients (Section 5.10), some do not.

When spatially and spectrally resolved X-ray surface brightness measurement are available, it will be possible to directly determine the mass profiles of clusters of galaxies and determine the distribution of the missing mass. The same method can be applied to the X-ray emitting gas in elliptical galaxies (Section 5.8). This capability should become available with the launch of AXAF (Chapter 6). Until that time, the present results on the distribution of the missing mass must be regarded as tantalizing but tentative.