Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by Annual Reviews. All rights reserved

3. POWER SPECTRUM

3.1. Power Spectrum on Large Scales

Let us take the power spectrum of primordial fluctuations to be a power law in comoving wavenumber k. In the "processed" radiation power spectrum, this simple power law is multiplied by a transfer function T²(k). On COBE scales T(k) 1, and we can write the temperature fluctuation power spectrum as

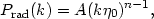
(12)

where A is the amplitude for scalar perturbations and ₀ 3t₀ = 2H₀^-1 (for ₀ = 1) is the conformal time today with scale factor normalized to unity. By using k₀ as our fundamental variable, we have A as a dimensionless number multiplied by something of order 10^{n - 1} on COBE scales. The connection between A and the normalization of the matter power spectrum is discussed in Section 3.3. [Another common convention is to define the matter power spectrum as P_mat(k) = Bkⁿ on large scales, which means that the dimensions of B will depend on n (and will be length⁴ for n = 1); see Equation (24).]

We can write the average over universes of the moments of the temperature anisotropy as

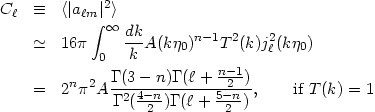
(13) (14) (15)

(see e.g. Peebles 1982c, Bond & Efstathiou 1987). For the special case of n = 1, we have C₂/A = 4/3 and C^-1 ( + 1). This is often referred to as "flat" since potential fluctuations (and the amplitude of / at horizon crossing) are independent of scale, and it also makes ( + 1) C = constant.

In some older literature, the normalization of the power spectrum is given in terms of _H, the dimensionless amplitude of matter fluctuations at horizon crossing. For a flat spectrum this quantity is simply _H² = (4/)A.

The normalization convention used by the COBE group, Q_{rms - PS} is obtained by a best fit to the correlation function assuming a flat spectrum of fluctuations and allowing the normalization to vary. In terms of C₂, this corresponds to

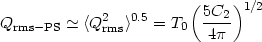
(16)

[For n = 1 the factor in parenthesis is (5/3)A, which allows a simple conversion from quadrupole normalization to our normalization in terms of A.] We would like to stress that Q_{rms - PS} is the COBE group's best estimate, measured from our sky, of the power spectrum normalization. It is not the quadrupole measured by the COBE team from their maps. The value quoted for Q_{rms - PS}, including the effects of systematic error, is (Smoot et al 1992, Wright et al 1994a, Bennett et al 1994)

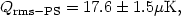
which implies

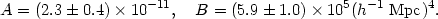
(17)

Since the analysis for Q_{rms - PS} assumed a flat spectrum, one should not use (17) to normalize other spectra, although <Q_rms²>^0.5 is still a valid way of quoting the normalization of the power spectrum.

For the first year data, a fit to the correlation function gives n = 1.1 ± 0.5 (Smoot et al 1992). Including the second year data gives n 1.5 - 0.5 (Bennett et al 1994, Wright et al 1994b) [by combining both COBE and Tenerife data, a stronger limit n 0.9 has been obtained (Hancock et al 1994)] and the inferred value of Q_{rms - PS} is quite correlated with a (Seljak & Bertschinger 1993, Watson & Gutierrez de la Cruz 1993). For n 1 the best value for the normalization is (Smoot et al 1992)

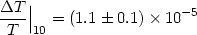
(18)

which probes a range of centered around 4 (Wright et al 1994a). Note that for n = 1, these two normalizations differ by ~ 10%, since the fit to Q_{rms - PS} uses the full correlation function.

Another normalization sometimes used is the bias, defined through

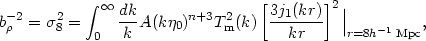
(19)

where T_m(k) is a matter transfer function (see later section) not to be confused with T(k), and ²(r) is the variance of the density field within spheres of radius r. The variance of galaxies, possibly biased relative to the matter (_gal = b ), is roughly unity on a scale of 8 h^-1 Mpc (Davis & Peebles 1983). Equation (19) is nontrivial to evaluate numerically because of the "ringing" of the j₁ and the final result is dependent on the transfer function assumed. For CDM, we will take (Efstathiou 1990)

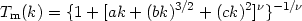
(20)

with a = 6.4₀ h^-2 Mpc, b = 3₀ h^-2 Mpc, c = 1.7₀ h^-2 Mpc, and = 1.13. We will set ₀ = 1 and h = 1/2 unless otherwise noted. For n = 1 the COBE best fit gives ₈ 1.2, i.e. an essentially unbiased model. However, this depends on the adopted values of ₀, h, etc. It is possible to have a nonstandard (e.g. 0.8) CDM model with the galaxies significantly biased on small scales as seems to be required (e.g. Davis et al 1985, Bardeen et al 1986, Frenk et al 1990, Carlberg 1991).

Large-scale flows also provide a measure of the power spectrum (Peebles 1993):

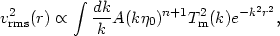
(21)

where v_rms is the 3-D velocity dispersion smoothed with a Gaussian filter of width r. This tends to probe scales similar to the degree-scale CMB experiments. Whether there is agreement between the two measures for a particular theory is still a matter of debate (see e.g. Vittorio & Silk 1985; Juszkiewicz et al 1987; Suto et al 1988; Atrio-Barandela et al 1991; Kashlinsky 1991, 1992, 1993a; Górski 1991, 1992).