Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by Annual Reviews. All rights reserved

3.2. Power Spectra on Smaller Scales

Although on large angular scales the transfer function is T(k) 1, there is significant structure on small to intermediate scales. Generally the Sachs-Wolfe effect dominates the power spectrum on scales larger than the horizon size at last scattering and the power spectrum can be taken to be a power law. On smaller scales, however, causal interactions become important and the spectrum is modified.

For a given cosmological model, the shape of the fluctuation spectrum is fixed, and depends on the primordial spectrum (e.g. kⁿ) and its evolution as the waves enter the horizon. This makes the spectrum at smaller scales dependent on ₀, _B, H₀, and the dark matter. Given a cosmological model, however, both the radiation and matter power spectra are well defined. For a fixed ₀, the radiation power spectrum depends only on the type of dark matter at the high k end.

The calculation proceeds by considering perturbations in the photon distribution function, f (x, q, t), which can be written in terms of

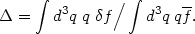
(22)

where 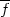is the Planck function and q is the comoving photon momentum. is the total energy, or brightness, perturbation, which is also 4T / T for a uniform shift in temperature. Liouville's theorem tells us that the total phase space density is conserved for collisionless particles, i.e. the distribution function is constant along particle paths: Df /Dt = 0. Source terms ("collisions") add on the right hand side; the important sources are baryon velocities and photon density perturbations coupled through Thomson scattering. The Boltzmann equation (or equation of radiative transfer, written here in the synchronous gauge) for is

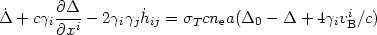
(23)

(see Peebles & Yu 1970, Hu et al 1994, Dodelson & Jubas 1994), where the dot denotes differentiation with respect to conformal time (= dt / a), _i are the direction cosines defined by 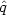, n_e is the number density of free electrons, a(t) is the cosmological scale-factor, v_B is the baryon peculiar velocity, ₀ is the isotropic part of , h_ij is the metric perturbation, and isotropic scattering has been assumed. The Boltzmann equation is generally Fourier transformed, since in the linear approximation the different k-modes evolve independently, which makes the calculation tractable. It is also assumed that all fluctuations are still in the linear regime, which is a reasonable approximation for the relevant scales at the scattering epoch. Since the effects of the radiation on the matter cannot be ignored (except for late reionization), the equation of motion for the baryons needs to be solved simultaneously; this is the continuity equation for matter evolving freely, but also takes into account the Compton drag at early times.

The radiation and baryons evolve as a coupled fluid at early times, but need to be followed more accurately as the Universe recombines, and eventually the baryons decouple from the photons entirely. After this point, the photons can be assumed to free-stream to the observer, and the subsequent behavior of the anisotropies is often treated analytically. Dark matter evolves collisionlessly throughout. although its gravity feeds back into the baryon and photon evolution. Detailed calculations along these lines have been carried out for many different cosmological models, e.g. the work of Peebles & Yu (1970), Wilson & Silk (1981), Bond & Efstathiou (1984, 1987), Vittorio & Silk (1984, 1992), Holtzman (1989), Sugiyama & Gouda (1992), Dodelson & Jubas (1993a), Stompor (1993), and Crittenden et al (1993a, b) among others. The Boltzmann equation is usually solved by expanding the s in Legendre polynomials up to some high enough and numerically integrating the coupled equations.

We show in Figure 2 the power spectrum for CDM models as a function of wavenumber k, for a range of _B consistent with Big Bang Nucleosynthesis (BBN) (Krauss & Romanelli 1990, Walker et al 1991, Smith et al 1993). To calculate the C from these power spectra approximately, one integrates the power spectrum with measure j²(k ₀) dk / k. Each C is thus in effect an average of the power spectrum around k H₀/2. We have also included an x_e = 1 reionized BDM power spectrum (arbitrarily normalized) on the figure for comparison.

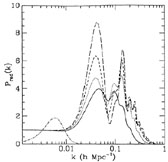
Figure 2. Power spectrum for "standard" CDM models (h = 1/2, 0 = 1 and = 0) with B = 0.01 (solid), 0.03 (dotted), 0.06 (short dashed) and 0.10 (long-dashed) consistent with the range from BBN, from Sugiyama & Gouda (1992). The curves have been normalized to unity at small k. For comparison we also show a fully ionized BDM model (dot-dashed line) with 0 = 0.1, n = 0, and h = 0.5, chosen (arbitrarily) to match at k = 0.002h Mpc-1.

The plateau in Figure 2 at low k is the contribution from the Sacks-Wolfe effect (or gravitational redshift), which damps on the scale of the scattering surface thickness. The bumps and wiggles reflect the phase of the oscillating baryons and photons when recombination occurs, i.e. the number of oscillations a given mode has undergone in the time between entering the horizon and the switch-off of radiation pressure when the matter becomes neutral. These so-called "Doppler" peaks (physically they come from a combination of v and sources which are difficult to separate) rise at k ~ 0.01 Mpc, the size of the horizon at the time of last scattering. In -space the rise to the first Doppler peak is quite gradual, which can lead an effective n > 1 even on relatively large scales, e.g. n_eff 1.15 on COBE scales (Bond 1994). The height of the Doppler peaks is dependent on the number of scatterers or _B h² (scaling roughly as _B^1/3, which would be the dependence for an experiment like MAX; see also Fukugita et al 1990). The second and third peaks are harmonics of the first which is the fluctuation that underwent half an oscillation since it entered the horizon. The amplitude of these oscillations reflects the amount of growth before the perturbation enters the photon-baryon Jeans scale, which depends on _B h². There is a further dependence on h through z_eq. There is also an effect due to the baryons falling into the dark matter potential wells after recombination, although this happens largely after the photons have been scattered. CDM fluctuations that first entered the horizon during radiation domination suffer growth suppression, which partly accounts for the differing heights of the peaks. Note, also, the exponential cutoff in the power spectrum at large k, due to the effects of the thickness of the last scattering surface, as well as the familiar damping (Silk 1968) of baryon and photon fluctuations prior to decoupling. The damping scale is set by the thickness z (see Appendix A).

For a reionized model (see Section 5.1) the visibility function is centered around some z_* and has width z ~ z_*, so that the two important scales above are almost the same. The effect is that there is only one Doppler peak, which is at the scale of the horizon at z_* (i.e. smaller k or ), with damping for higher wavenumbers. There are no extra bumps and wiggles, since at the time of last scattering the photons and baryons were no longer oscillating.