2.2.1. Mathematical Details

We now describe the method in detail. We assume that the relevant distance indicator is the TF relation; with minor changes, the formalism could be adapted to comparable distance indicators such as D_n - . We use the terminology of Willick (1994) and Willick et al. (1995): briefly, we denote by m and log v_rot - 2.5 a galaxy's corrected apparent magnitude and velocity width parameter, respectively; by cz, its Local Group frame radial velocity ("redshift") in units of km s^-1; and by r, its true distance in units of km s^-1. We define the distance modulus as µ 5 log r, and absolute magnitudes as M = m - µ. We write the forward and inverse TF relations as linear expressions, M() = A - b and ⁰(M) = -e(M - D), and denote their rms scatters _TF and , respectively.

We seek an exact expression for the probability that a galaxy at redshift cz possesses TF observables (m, ), given a model of the peculiar velocity and density fields. ⁽⁵⁾ We first consider the joint probability distribution of the TF observables, redshift, and an unobservable quantity, the true distance r. Later, we will integrate over r to obtain the probability distribution of the observables. We may write

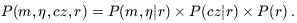
(5)

The splitting into conditional probabilities reflects the fact that the TF observables and the redshift couple with one another only via their individual dependences on the true distance r.

The first of the three terms on the right-hand side of equation (5) depends on the luminosity function, the sample selection function, and the TF relation. We can express it in one of two ways, depending on whether we are using the forward or inverse form of the TF relation:

1. Forward relation:

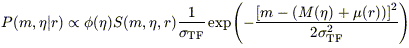
(6)

2. Inverse relation:

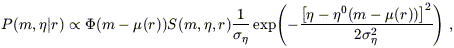
(7)

where () and (M) are the (closely related) velocity width distribution function and luminosity function, respectively, and S(m, , r) is the sample selection function; we have assumed Gaussian scatter of the TF relation (cf. the discussion in Section 4.1).

Detailed derivations of these expressions are given by Willick (1994). ⁽⁶⁾ In equations (6) and (7), we have written only proportionalities, since the normalization is straightforward and will occur at a later point in any case.

The third term on the right-hand side of equation (5) is simply the a priori probability of observing an object at distance r,

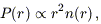
(8)

where n(r) 1 + _g(r) is the number density of the species of galaxies that makes up the sample. The second term on the right-hand side of equation (5), P(cz|r), is the one that couples the TF observables to the velocity field model. We assume that, for the correct IRAS velocity field reconstruction (i.e., for the correct value of _I and other velocity field parameters, to be described below), the redshift is normally distributed about the value predicted from the velocity model:

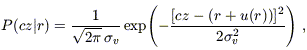
(9)

where u(r) 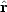^. [v(r) - v(0)] is the radial component of the predicted peculiar velocity field in the Local Group frame (cf. eq. [A1]). We treat the velocity noise _v as a free parameter in our analysis; we discuss its origin in detail in Section 3.2. Although _v must be position or density dependent at some level, we treat it as spatially constant in this paper, except in the Virgo Cluster (Section 4.3). The present data do not enable us to model the possible position or density dependence of _v in terms of free parameters.

Substituting equations (6) (or eq. [7]), (8), and (9) into equation (5) yields the joint probability distribution P(m, , cz, r). To obtain the joint probability distribution of the observable quantities, one integrates over the (unobserved) line-of-sight distance, i.e.,

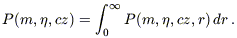
(10)

In practice, it is not optimal to base a likelihood analysis on the joint distribution P(m, , cz) because of its sensitivity to terms, such as the luminosity function, the sample selection function, and the density field, that are not critical for our purposes. Instead, the desired probability distributions are the conditional ones:

1. Forward TF relation:

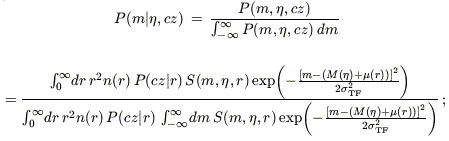
(11)

2. Inverse TF relation:

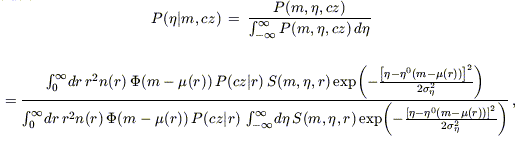
(12)

where P(cz|r) is given by equation (9).

Although neither of these expressions is independent of the density field n(r) or the selection function S, their appearance in both the numerator and the denominator much reduces their sensitivity to them. A similar statement holds for the luminosity function in equation (12). The velocity width distribution function , however, has dropped out entirely from the forward relation probability. We discuss these points further in Section 2.2.2.

Equations (11) and (12) are the conditional probabilities whose products we wish to maximize over all the galaxies in the sample. In practice, we do so by minimizing the quantities

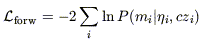
(13)

or

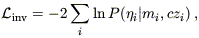
(14)

where the index i runs over all the objects in the TF sample. We have assumed that the probabilities for each galaxy are independent; we validate this assumption a posteriori (cf. Section 5.2).

⁵ The dependence of all quantities on the line-of-sight direction will remain implicit. Back.

⁶ Willick (1994) assumed that the selection function depended on the TF observables only. Here we acknowledge the possibility of an explicit distance dependence; the origin of such a dependence was discussed by SW, Section 6.5.3. Back.