


Most gravitational lenses have the standard configurations we illustrated in Section B.2. These configurations are easily understood in terms of the caustic structures generic to simple lens models. In this section we illustrate the origin of these basic geometries using simple mathematical examples. We build on the general outline of lensing theory from Part 1.
B.3.1. Some Nomenclature
Throughout this lecture we use comoving angular diameter distances (also
known as proper motion distances) rather than the
more familiar angular diameter distances because almost every
equation in gravitational lensing becomes simpler. The distance between
two redshifts i and j is
where
for flat universes.
We denote angles on the lens plane by
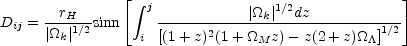
(B.1)
 M,
M,

 and
and
 k = 1 -
k = 1 -
 M -
M -

 are
the present day matter density, cosmological constant and "curvature"
density respectively, rH = c /
H0 is the Hubble radius, and the function
sinn(x) becomes sinh(x), x or sin(x)
for open
(
are
the present day matter density, cosmological constant and "curvature"
density respectively, rH = c /
H0 is the Hubble radius, and the function
sinn(x) becomes sinh(x), x or sin(x)
for open
( k >
0), flat
(
k >
0), flat
( k = 0) and
closed
(
k = 0) and
closed
( k < 0)
models (Carroll, Press & Turner
[1992]).
We use Dd, Ds and
Dds for the distances from the observer to the lens,
from the observer to the source and from the lens to the source. These
distances are trivially related to the angular diameter distances,
Dijang = Dij / (1 +
zj), and luminosity distances,
Dijlum = Dij(1 +
zj). In a flat universe, one can simply add comoving
angular diameter distances (Ds = Dd
+ Dds), which is not true of angular diameter
distances. The comoving volume element is
k < 0)
models (Carroll, Press & Turner
[1992]).
We use Dd, Ds and
Dds for the distances from the observer to the lens,
from the observer to the source and from the lens to the source. These
distances are trivially related to the angular diameter distances,
Dijang = Dij / (1 +
zj), and luminosity distances,
Dijlum = Dij(1 +
zj). In a flat universe, one can simply add comoving
angular diameter distances (Ds = Dd
+ Dds), which is not true of angular diameter
distances. The comoving volume element is
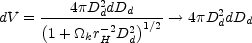
(B.2)
 =
=  (cos
(cos ,
sin
,
sin ) and
angles on the source plane by
) and
angles on the source plane by
 .
Physical lengths on the lens plane are
.
Physical lengths on the lens plane are
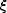 =
Ddang
=
Ddang
 . The
lensing potential, denoted by
. The
lensing potential, denoted by
 (
( ), satisfies
the Poisson equation
), satisfies
the Poisson equation
 2
2
 =
2
=
2 where
where
 =
=
 /
/
 c is the
surface density
c is the
surface density
 in units of the
critical surface density
in units of the
critical surface density
 c =
c2(1 + zl) Ds /
(4
c =
c2(1 + zl) Ds /
(4 G Dd
Dds). For a
more detailed review of the basic physics, see Part 1.
G Dd
Dds). For a
more detailed review of the basic physics, see Part 1.