B.4.2. The Effective Single Screen Lens

Throughout these notes we will treat lenses as if all the lens components lay at a single redshift ("the single screen approximation"). The lens equations for handling multiple deflection screens (e.g. Blandford & Narayan [1986], Kovner [1987b], Barkana [1996]) are known but little used except for numerical studies (e.g. Kochanek & Apostolakis [1998], Moller & Blain [2001]) in large part because few lenses require multiple lens galaxies at different redshifts with the exception of B2114+022 (Chae, Mao & Augusto [2001]). In fact, we are not being as cavalier in making this approximation as it may seem.

The vast majority of strong lenses consist of a single lens galaxy perturbed by other objects. We can divide these objects into those near the primary lens, where a single screen is clearly appropriate, and those distributed along the line of site for which a single screen may be inappropriate. Because the correlation function is so strong on small scales, the perturbations are dominated by objects within a correlation length of the lens galaxy (e.g. Keeton, Kochanek & Seljak [1997], Holder & Schechter [2003]). The key to the relative safety of the single screen model is that weak perturbations from objects along the line of site, in the sense that in a multi-screen lens model they could be treated as a convergence and a shear, can be reduced to a single "effective" lens plane in which the true amplitudes of the convergence and shear are rescaled by distance ratios to convert them from their true redshifts to the redshift of the single screen (Kovner [1987b], Barkana [1996]). The lens equation on the effective single screen takes the form

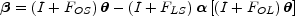(B.63)

where F_OS, F_LS and F_OL describe the shear and convergence due to perturbations between the observer and the source, the lens and the source and the observer and the lens respectively. For statistical calculations this can be simplified still further by making the coordinate transformation  ' = (I + F_OL) and  ' = (I + F_LS) ) to leave a lens equation,

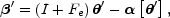(B.64)

identical to a single screen lens in an effective convergence and shear of F_e = F_OL + F_LS - F_OS (to linear order). In practice it will usually be safe to neglect the differences between Eqns. B.63 and B.64 because the shearing terms affecting the deflections in Eqn B.63 are easily mimicked by modest changes in the ellipticity and orientation of the primary lens. The rms amplitudes of these perturbations depend on the cosmological model and the amplitude of the non-linear power spectrum, but the general scaling is that the perturbations grow as D_s^3/2 with source redshift, and increase for larger ₈ and _M as shown in Fig. B.19 from Keeton et al. ([1997]). The importance of these effects is very similar to concerns about the effects of lenses along the line of sight on the brightness of high redshift supernova being used to estimate the cosmological model (e.g. Dalal et al. [2003]).

Figure B.19. Dependence of the shear generated by other objects along the line of sight for both linear (light lines) and non-linear (heavy lines) power spectra. (a) Shows the logarithmic contribution to the rms effective shear for a source at redshift zs = 3 as a function of wave vector k. (b) Shows the dependence on 8 for a fixed power spectrum shape M h = 0.25. (c) Shows the dependence on the shape Mh with 8 = 0.6 for M = 1 and 8 = 1.0 for M < 1. (d) Shows the variation in the shear with source redshift for the models in (c) with M h = 0.25.