


B.4.1. Common Models for the Monopole
Most attention in modeling lenses focuses on the monopole or radial mass distribution of the lenses. Unfortunately, much of the lensing literature uses an almost impenetrable array of ghastly non-standard acronyms to describe the mass models even though many of them are identical to well-known families of density distributions used in stellar dynamics. Here we summarize the radial mass distributions which are most commonly used and will keep reappearing in the remainder of Part 2.
The simplest possible choice for the mass distribution is to simply trace the light. The standard model for early-type galaxies or the bulges of spiral galaxies is the de Vaucouleurs ([1948]) profile with surface density
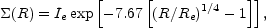 |
(B.53) |
where the effective radius Re encompasses half the total mass (or light) of the profile. Although the central density of a de Vaucouleurs model is finite, it actually acts like a rather cuspy density distribution and will generally fit the early-type lens data with no risk of producing a detectable central image (e.g. Lehár et al. [2000], Keeton [2003a]). The simplest model for a disk galaxy is an exponential disk,
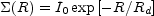 |
(B.54) |
where Rd is the disk scale length. An exponential disk by itself is rarely a viable lens model because it has so little density contrast between the center and the typical radii of images that detectable central images are almost always predicted but not observed. Some additional component, either a de Vaucouleurs bulge or a cuspy dark matter halo, is always required. This makes spiral galaxy lens models difficult because they generically require two stellar components (a bulge and a disk) and a dark matter halo, while the photometric data are rarely good enough to constrain the two stellar components (e.g. Maller, Flores & Primack [1997], Koopmans et al. [1998], Maller et al. [2000], Trott & Webster [2002], Winn, Hall & Schechter [2003]). Since spiral lenses are already relatively rare, and spiral lens galaxies with good photometry are rarer still, less attention has been given to these systems. The de Vaucouleurs and exponential disk models are examples of Sersic ([1968]) profiles
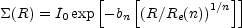 |
(B.55) |
where the effective radius Re(n) is defined to encompass half the light and n = 4 is a de Vaucouleurs model and n = 1 is an exponential disk. These profiles have not been used as yet for the study of lenses except for some quasar host galaxy models (Section B.10). The de Vaucouleurs model can be approximated (or the reverse) by the Hernquist ([1990]) model with the 3D density distribution
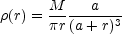 |
(B.56) |
and a  0.55Re if matched to a de Vaucouleurs model.
For lensing purposes, the Hernquist model has one major problem. Its
0.55Re if matched to a de Vaucouleurs model.
For lensing purposes, the Hernquist model has one major problem. Its

 1 / r central
density cusp is shallower than the effective cusp of a de Vaucouleurs
model, so Hernquist models tend to predict detectable
central images even when the
matching de Vaucouleurs model would not. As a result, the Hernquist model
is more often used as a surrogate for dynamical normalization of the de
Vaucouleurs model than as an actual lens model (see below).
1 / r central
density cusp is shallower than the effective cusp of a de Vaucouleurs
model, so Hernquist models tend to predict detectable
central images even when the
matching de Vaucouleurs model would not. As a result, the Hernquist model
is more often used as a surrogate for dynamical normalization of the de
Vaucouleurs model than as an actual lens model (see below).
Theoretical models for lenses started with simple, softened power laws of the form
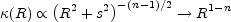 |
(B.57) |
in the limit where there is no core radius. We are using these simple power law lenses in all our examples (see Section B.3). These models include many well known stellar dynamical models such as the singular isothermal sphere (SIS, n = 2, s = 0), the modified Hubble profile (n = 3) and the Plummer model (n = 5). Since we only see the projected mass, these power laws are also related to common models for infinitely thin disks. The Mestel ([1963]) disk (n = 2, s = 0) is the disk that produces a flat rotation curve, and the Kuzmin ([1956]) disk (n = 3) can be used to mimic the rising and then falling rotation curve of an exponential disk. The softened power-law models have generally fallen out of favor other than as simple models for some of the visible components of lenses because the strong evidence for stellar and dark matter cusps makes models with core radii physically unrealistic. While ellipsoidal versions of these models are not available in useful form, there are fast series expansion methods for numerical models (Chae, Khersonsky & Turnshek [1998], Barkana [1998]).
Most "modern" discussions of galaxy density distributions are based on sub-cases of the density distribution
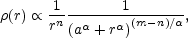 |
(B.58) |
which has a central density cusp with

 r-n, asymptotically declines as
r-n, asymptotically declines as

 r-m
and has a break in the profile near r
r-m
and has a break in the profile near r
 a
whose shape depends on
a
whose shape depends on
 (e.g. Zhao
[1997]).
The most common cases are the Hernquist model (n = 1, m = 4,
(e.g. Zhao
[1997]).
The most common cases are the Hernquist model (n = 1, m = 4,
 = 1) mentioned above,
the Jaffe
([1983])
model (n = 2, m = 4,
= 1) mentioned above,
the Jaffe
([1983])
model (n = 2, m = 4,
 = 1), the NFW (Navarro,
Frenk & White
[1996])
model (n = 1, m = 3,
= 1), the NFW (Navarro,
Frenk & White
[1996])
model (n = 1, m = 3,
 = 1) and the Moore
([1998]) model
(n = 3/2, m = 3,
= 1) and the Moore
([1998]) model
(n = 3/2, m = 3,
 = 1). We can view the
power-law models either as the limit
n
= 1). We can view the
power-law models either as the limit
n  0 and
0 and
 = 2, or we could
generalize the r-n term to
(r2 + s2)-n/2 and consider
only regions with r and s << a. Projections
of these models are similar to surface density distributions of the form
= 2, or we could
generalize the r-n term to
(r2 + s2)-n/2 and consider
only regions with r and s << a. Projections
of these models are similar to surface density distributions of the form
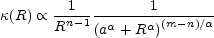 |
(B.59) |
(although the definition of the break radius a changes) with the
exception of the limit
n  1 where the
projection of a 3D density cusp
1 where the
projection of a 3D density cusp

 1 / r produces
surface density terms
1 / r produces
surface density terms 
 ln R that
cannot be reproduced by the broken surface
density power law. This surface density model is sometimes called the
Nuker law (e.g. Byun et al.
[1996]).
A particularly useful case for lensing is the pseudo-Jaffe model with
n = 2, m = 4 and
ln R that
cannot be reproduced by the broken surface
density power law. This surface density model is sometimes called the
Nuker law (e.g. Byun et al.
[1996]).
A particularly useful case for lensing is the pseudo-Jaffe model with
n = 2, m = 4 and
 = 2 (where the normal
Jaffe model has
= 2 (where the normal
Jaffe model has
 = 1) as the only
example of a broken power law with simple analytic
deflections even when ellipsoidal because the density distribution is
the difference between two isothermal ellipsoids (see Eqn. B.41).
These cuspy models also allow fast approximate solutions for their
ellipsoidal counterparts (see
Chae 2002).
= 1) as the only
example of a broken power law with simple analytic
deflections even when ellipsoidal because the density distribution is
the difference between two isothermal ellipsoids (see Eqn. B.41).
These cuspy models also allow fast approximate solutions for their
ellipsoidal counterparts (see
Chae 2002).
The most theoretically important of these cusped profiles is the NFW profile (Navarro et al. 1996) because it is the standard model for dark matter halos. Since it is such a common model, it is worth discussing it in a little more detail, particularly its peculiar normalization. The NFW profile is normalized by the mass Mvir inside the virial radius rvir, with
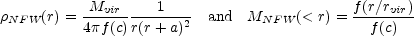 |
(B.60) |
where f (c) = ln(1 + c) - c / (1 + c) and
the concentration c = rvir / a ~ 5 for
clusters and c ~ 10 for galaxies. The concentration is a function
of mass whose scaling is determined from N-body simulations. A typical
scaling for a halo at redshift z in an
 M = 0.3
flat cosmological models is
(Bullock et al. 2001)
M = 0.3
flat cosmological models is
(Bullock et al. 2001)
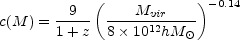 |
(B.61) |
with a dispersion in log c of
 log c
log c
 0.18 dex. Because
gravitational lensing is very sensitive to the central density of the lens,
including the scatter in the concentration is quantitatively important for
lensing by NFW halos (Keeton
[2001b]).
The virial mass and radius are related and determined by the overdensity
0.18 dex. Because
gravitational lensing is very sensitive to the central density of the lens,
including the scatter in the concentration is quantitatively important for
lensing by NFW halos (Keeton
[2001b]).
The virial mass and radius are related and determined by the overdensity
 vir(z) required
for a halo to collapse given the cosmological model and the
redshift. This can be approximated by
vir(z) required
for a halo to collapse given the cosmological model and the
redshift. This can be approximated by
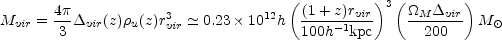 |
(B.62) |
where  u(z) = 3H02
u(z) = 3H02
 M(1 +
z)3 /
8
M(1 +
z)3 /
8 G is the mean matter
density when the halo forms and
G is the mean matter
density when the halo forms and
 vir
vir
 (18
(18 2 + 82x -
39x2) /
2 + 82x -
39x2) /
 (z) with
x =
(z) with
x =  - 1 is
the overdensity needed for a halo to collapse. There
are differences in normalizations between authors and with changes in the
central cusp exponent
- 1 is
the overdensity needed for a halo to collapse. There
are differences in normalizations between authors and with changes in the
central cusp exponent
 , but
models of this type are what we presently
expect for the structure of dark matter halos around galaxies.
, but
models of this type are what we presently
expect for the structure of dark matter halos around galaxies.
For most lenses, HST imaging allows us to measure the spatial distribution of the stars, thereby providing us with a model for the distribution of stellar mass with only the stellar mass-to-light ratio as a parameter. For present purposes, gradients in the stellar mass-to-light ratio are unimportant compared to the uncertainties arising from the dark matter. Unless we are prepared to abandon the entire paradigm for modern cosmology, the luminous galaxy is embedded in a dark matter halo and we must decide how to model the overall mass distribution. The most common approach, as suggested by the rich variety of mass profiles we introduced in Section B.4.1, is to assume a parametric form for the total mass distribution rather than attempting to decompose it into luminous and dark components. The alternative is to try to embed the stellar component in a dark matter halo. Operationally, doing so is trivial - the lens is simply modeled as the sum of two mass components. However, there are theoretical models for how CDM halos should be combined with the stellar component.
Most non-gravitational lensing applications focus on embedding disk galaxies in halos because angular momentum conservation provides a means of estimating a baryonic scale length (e.g. Mo, Mao & White [1998]). The spin parameter of the halo sets the angular momentum of the baryons, and the final disk galaxy is defined by the exponential disk with the same angular momentum. As the baryons become more centrally concentrated, they pull the dark matter inwards as well through a process known as adiabatic contraction (Blumenthal et al. [1986]). The advantage of this approach, which in lensing has been used only by Kochanek & White ([2001]), is that it allows a full ab initio calculation of lens statistical properties when combined with a model for the cooling of the baryons (see Section B.7). It has the major disadvantage that most lens galaxies are early-type galaxies rather than spirals, and that there is no analog of the spin parameter and angular momentum conservation to set the scale length of the stellar component in a model for an early-type galaxy.
Models of early-type galaxies embedded in CDM halos have to start with an empirical estimate of the stellar effective radius. In models of individual lenses this is a measured property of the lens galaxy (e.g. Rusin et al. [2003], [2004], Koopmans & Treu [2002], Kochanek [2003a]). Statistical models must use a model for the scaling of the effective radius with luminosity or other observable parameters of early-type galaxies (e.g. Keeton [2001b]). From the luminosity, a mass-to-light ratio is used to estimate the stellar mass. If all baryons have cooled and been turned into stars, then the stellar mass provides the total baryonic mass of the halo, otherwise the stellar mass sets a lower bound on the baryonic mass. Combining the baryonic mass with an estimate of the baryonic mass fraction yields the total halo mass to be fed into the model for the CDM halo.
In general, there is no convincing evidence favoring either approach - for the regions over which the mass distributions are constrained by the data, both approaches will agree on the overall mass distribution. However, there can be broad degeneracies in how the total mass distribution is decomposed into luminous and dark components (see Section B.4.6).