


B.4.7. Non-Parametric Models
The basic idea behind non-parametric mass models is that the effective
lens potential and the deflection equations are linear "functions" of the
surface density. The surface density can be decomposed into multipoles
(Kochanek
[1991a],
Trotter, Winn & Hewitt
[2000],
Evans & Witt
[2003]),
pixels (see Saha & Williams
[1997],
[2004],
Williams & Saha
[2000]),
or any other form in which
the surface density is represented as a linear combination of density
functionals multiplied by unknown coefficients
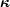 . In any
such model, the lens equation for image i takes the form
. In any
such model, the lens equation for image i takes the form
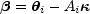 |
(B.85) |
where Ai is the matrix that gives the deflection at
the position of image i in terms of the coefficients of the
surface density decomposition
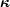 . For a lens
with i = 1 ... n images
of the same source, such a system can be solved exactly if there are
enough degrees of freedom in the description of the surface density.
For simplicity, consider a two-image lens so that we can eliminate
the source position by hand, leaving the system of equations
. For a lens
with i = 1 ... n images
of the same source, such a system can be solved exactly if there are
enough degrees of freedom in the description of the surface density.
For simplicity, consider a two-image lens so that we can eliminate
the source position by hand, leaving the system of equations
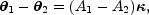 |
(B.86) |
which is easily solved by simply taking the inverse of the matrix A1 - A2 to find that
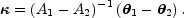 |
(B.87) |
Sadly, life is not that simple because as soon as the density decomposition has more degrees of freedom than there are constraints, the inverse (A1 - A2)-1 of the deflection operators is singular.
The solution to this problem is to instead consider the problem as a
more general minimization problem with a
 2 statistic for the
constraints and some form of regularization to restrict the results to
plausible surface densities. One possibility is linear regularization,
in which you minimize the function
2 statistic for the
constraints and some form of regularization to restrict the results to
plausible surface densities. One possibility is linear regularization,
in which you minimize the function
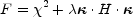 |
(B.88) |
where the  2
measures the goodness of fit to the lens constraints,
H is a weight matrix and
2
measures the goodness of fit to the lens constraints,
H is a weight matrix and
 is a Lagrange
multiplier. The
Lagrange multiplier controls the relative importance given to fitting the
lens constraints (minimizing the
is a Lagrange
multiplier. The
Lagrange multiplier controls the relative importance given to fitting the
lens constraints (minimizing the
 2) versus
producing a smooth density distribution (minimizing
2) versus
producing a smooth density distribution (minimizing
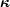 . H .
. H .
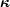 ).
The simplest smoothing function is to minimize the variance of the
surface density (H = I, the identity matrix), or,
equivalently, ignore H and use the singular value
decomposition for inverting a singular matrix. By using more complicated
matrices you can
minimize derivatives of the density (gradients, curvature etc.). Solutions
are found by adjusting the multiplier
).
The simplest smoothing function is to minimize the variance of the
surface density (H = I, the identity matrix), or,
equivalently, ignore H and use the singular value
decomposition for inverting a singular matrix. By using more complicated
matrices you can
minimize derivatives of the density (gradients, curvature etc.). Solutions
are found by adjusting the multiplier
 until the goodness of
fit satisfies
until the goodness of
fit satisfies  2
2
 Ndof
where Ndof is the number of degrees of freedom.
Another solution is to use linear programming methods to impose constraints
such as positive surface densities, negative density gradients from the lens
center or density symmetries (Saha & Williams
[1997],
[2004],
Williams & Saha
[2000]).
Time delays, which are also linear
functions of the surface density, are easily included. Flux ratios are
more challenging because magnifications are quadratic rather than linear
functions of the surface density except for the special case of the
generalized singular isothermal models where
Ndof
where Ndof is the number of degrees of freedom.
Another solution is to use linear programming methods to impose constraints
such as positive surface densities, negative density gradients from the lens
center or density symmetries (Saha & Williams
[1997],
[2004],
Williams & Saha
[2000]).
Time delays, which are also linear
functions of the surface density, are easily included. Flux ratios are
more challenging because magnifications are quadratic rather than linear
functions of the surface density except for the special case of the
generalized singular isothermal models where
 = b
= b
 F(
F( )
(Eqn. B.42, Witt, Mao & Keeton
[2000],
Kochanek et al.
[2001],
Evans & Witt
[2001]).
The best developed, publicly available non-parametric models are those
by Saha & Williams
([2004]).
These are available at
http://ankh-morpork.maths.qmul.ac.uk/~saha/astron/lens/.
)
(Eqn. B.42, Witt, Mao & Keeton
[2000],
Kochanek et al.
[2001],
Evans & Witt
[2001]).
The best developed, publicly available non-parametric models are those
by Saha & Williams
([2004]).
These are available at
http://ankh-morpork.maths.qmul.ac.uk/~saha/astron/lens/.
Personally, I am not a fan of the non-parametric models, because
almost all the additional degrees of freedom they include are irrelevant
to the problem. As I have tried to outline in the preceding sections,
there is no real ambiguity about the aspects of gravitational potentials
either constrained or unconstrained by lens models. Provided the
parametric models capture these
degrees of freedom and you do not get carried away with the precision of the
fits, you can ignore deviations of the
cos(16 ) term of
the surface density
from that expected for an ellipsoidal model. Similarly
for the monopole profile, the distribution of mass interior and exterior
to the images is irrelevant and for the most part only the mean surface
density between
the images has any physical effect. Nothing is gained by allowing arbitrary,
fine-grained distributions.
) term of
the surface density
from that expected for an ellipsoidal model. Similarly
for the monopole profile, the distribution of mass interior and exterior
to the images is irrelevant and for the most part only the mean surface
density between
the images has any physical effect. Nothing is gained by allowing arbitrary,
fine-grained distributions.
There are also specific physical and mathematical problems with non-parametric models just as there are for parametric models. First, the trick of linearization only works if the lens equations are solved on the source plane. As we discussed when we introduced model fitting (Section B.4.6), this makes it impossible to properly compute error bars on any parameters. The equations become non-linear if they include either the magnification tensor (Eqn. B.83) or use the true image plane fit statistic (Eqn. B.84), and this greatly reduces the attractiveness of these methods. Second, in many cases the non-parametric models are not constrained to avoid creating extra images not seen in the observations - the models reproduce the observed images exactly, but come with no guarantee that they are not producing 3 other images somewhere else. Third, it is very difficult to guarantee that the resulting models are physical. For example, consider a simple spherical lens constrained to have positive surface density. For the implied three-dimensional density to also be positive definite, the surface density must decline monotonically from the center of the lens. This constraint is usually applied by the Saha & Williams ([2004]) method. For the distribution function of the stars making up the galaxy to be positive definite, the three dimensional density must also decline monotonically - this implies a constraint on the second derivative of the surface density which is not imposed by any of these methods. For the distribution to be dynamically stable it must satisfy a criterion on the derivative of the distribution function with respect to the orbital energy, and this implies a criterion on the third derivative of the surface density which is also not imposed (see Binney & Tremaine [1987]). Worse yet, for a non-spherical system we cannot even write down the constraints on the surface density required for the model to correspond to a stable galaxy with a positive definite distribution function. In short, most non-parametric models will be unphysical - they overestimate the degrees of freedom in the mass distribution. The critique being made, parametric models have a role because they define the outer limits of what is possible by avoiding the strong physical priors implicit in parametric models of galaxies.