B.7.1. The Effects of Halo Structure and the Power Spectrum

Estimating the structure of clusters using gravitational lensing is primarily a topic for Part 3, so we include only an abbreviated discussion of lensing by clusters here. For a fixed cosmological model, two parameters largely control the abundance of cluster lenses. First, the abundance of clusters varies nearly exponentially with the standard normalization ₈ 1 of the power spectrum on 8h^-1 Mpc scales. Second, the cross sections of the individual clusters depend strongly on the exponent of the central density cusp of the cluster. There are recent studies of these issues by Li & Ostriker ([2002], [2003]), Huterer & Ma ([2004]), Kuhlen, Keeton & Madau ([2004]), Oguri et al. ([2004]), and Oguri & Keeton ([2004]).

We can understand the general effects of halo structure very easily from our simple power law model in Eqn. B.9. In Section B.3 we normalized the models to have the same Einstein radius, but we now want to normalize them to all have the same total mass interior to some much larger radius R₀. This is roughly what happens when we keep the virial mass and break radius of the halo constant but vary the central density exponent r^-n. The deflection profile becomes

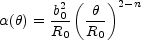(B.121)

where b₀ << R₀ sets the mass interior to R₀ and we recover our old example if we let b = b₀ = R₀. The typical image separation is determined by the tangential critical line at _t = R₀(b₀ / R₀)^2/(n-1), so more centrally concentrated lenses (larger n) produce larger image separations when b₀ / R₀ << 1. The radial caustic lies at _r = f (n) _t where f (n) is a not very interesting function of the index n, so the cross section for multiple imaging _r² R₀²(b₀ / R₀)^4/(n-1) - for an SIS profile b⁴ / R₀², while the cross section for a Moore profile (n = 3/2) b⁸ / 16R₀⁶ is significantly smaller. We cannot go to the limit of an NFW profile (n = 1) because our power law model has a constant surface density rather than a logarithmically divergent surface density in the limit as n 1, but we can see that as the density profile becomes shallower the multiple image cross section drops rapidly when the models have constant mass inside a radius which is much larger than their Einstein radius. As a result, the numbers of group or cluster lenses depends strongly on the central exponent of the density distribution even when the mass function of halos is fixed. Magnification bias will weaken the dependence on the density slope because the models with shallower slopes and smaller cross sections will generally have higher average magnifications. The one caveat to these calculations is that many groups or clusters will have central galaxies, and the higher surface density of the galaxy can make the central density profile effectively steeper than the CDM halo in isolation.