A century ago our picture of the cosmos was of a small, young, and static universe. Today we have a far grander and richer universe to inhabit, one that carries information on the strongest and weakest forces in nature, whose history runs from singularities and densities and temperatures far beyond our terrestrial and laboratory access to the vacuum and temperatures near absolute zero. Understanding our universe relies on a wide range of physics fields including thermodynamics, classical and quantum field theory, particle physics, and gravitation.
Perhaps most amazing is that while our universe is huge, it is finite in well defined ways, and can be encompassed and comprehended. The visible universe extends for nearly an equal number of orders of magnitude above the size of the Earth as the proton lies below. The number of particles is of order 1080, large but not unbounded, and the age of the universe is some 14 billion years, only three times the age of the Earth. And the universe is simple in ways we have no right to expect: it is essentially electrically neutral and its large scale dynamics is governed by gravity and no other forces of nature, it is nearly in thermal equilibrium for most of its history, and the geometry of space is maximally symmetric.
A few characteristics hold where we might be tempted to say, as Alfonso X "The Wise" did in the 13th century: "Had I been present at the creation of the world, I should have recommended something simpler". The universe has about a billion times more entropy per baryon than expected, and in a related sense has a greatly unequal ratio of matter to antimatter. The dynamics is neither kinetic energy dominated nor potential energy dominated but apparently perfectly balanced, giving the critical energy density and a flat spatial geometry. But the most important cosmological discovery of the 20th century was that the maximal symmetry does not extend to spacetime; that is, we do not live in a steady state universe unchanging in time.
Discovery of the cosmic expansion of space in the 1910s and 1920s and that the evolution arose from a hot, dense, early state called the Big Bang in the 1960s gave rise to modern cosmology as a exemplar of, window on, and laboratory for physics. Ten years ago the discovery of the acceleration of that expansion revolutionized cosmology and a great array of overlapping fields of physics. This article addresses our current knowledge of the cosmic expansion and our prospects for exploring it in detail. In particular, we focus on the recent epoch of acceleration and the astrophysical tools for mapping the cosmic expansion history to reveal the nature of new physics beyond our present standard model.
In the remainder of this section we discuss how the expansion of our universe impacts fundamental questions of the origin and fate of the cosmos and everything in it, and its intimate relation with the nature of gravity, as a force itself and reflecting on unification with quantum theory. We present the effects of acceleration in Section 2, but do not go into the root causes of it, which are highly speculative at this time; see, e.g., the focus issue on dark energy in [1]. Techniques for directly mapping the expansion appear in Section 3, while Section 4 briefly mentions indirect effects of acceleration through the growth of structure in the universe. Obtaining an accurate map is crucial to our understanding, and Section 5 focuses on challenges imposed by systematic uncertainties within the theoretical interpretation and data analysis. For future measurements these may be the key issues in advancing our knowledge. Future prospects for mapping the cosmic expansion from the Big Bang to the final fate are outlined in Section 6, and Section 7 summarizes and concludes.
In the 1910s the frequency shift of spectral lines from astronomical sources with respect to laboratory measurements were observed by Slipher and the dynamics of space was found by Einstein within his theory of general relativity. While Einstein, together with de Sitter, acted to counteract the expansion of space and retain a static state through introduction of the cosmological constant, other researchers in the 1920s such as Friedmann and Lemaître calculated the expansion history of a universe containing matter and components with pressure, and Weyl recognized that a physical expansion scaling linearly with distance occurred naturally. The observations of Hubble in 1929 established the expanding universe as the basis of cosmology.
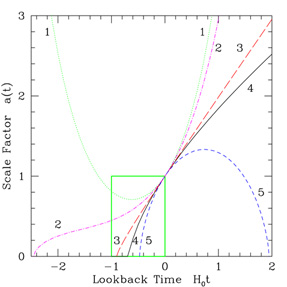
From the 1930s to 1980s, astronomical observations of the behavior of sources at different redshifts, and the increasing corroboration of redshift as directly related to distance, confirmed the picture of an expanding universe. (For a collection of some important early papers, see [2].) Figure 1 shows the evolution of our capabilities to map the cosmic expansion and the subsequent understanding achieved. Comparison of theoretical calculations and observations with respect to primordial nucleosynthesis and the cosmic microwave background (CMB) radiation clarified the model as one arising from a hot, dense, near singular state given the name Big Bang. However, estimates of the matter density (and even more so other component contributions, save for radiation measured directly in the CMB) remained somewhat vague, and in fact little different from Friedmann's 1922 work. Data could not make a definitive statement as to whether the matter and energy density amounted to less than, equal to, or possibly greater than the critical density needed for a spatially flat, asymptotically static expansion.
This all changed dramatically in 1998 with the discovery of acceleration of the cosmic expansion, by two independent groups mapping the distance-redshift relation of Type Ia supernovae [3, 4]. The expansion history behavior jumped from being somewhere between a critical, matter dominated universe and an open, spatial curvature dominated universe (approaching an empty universe akin to the Minkowski space of merely special relativity), and instead shifted toward one with similarities to de Sitter space governed by a cosmological constant. What was so revolutionary was not that such behavior merely changes the quantitative aspects of the expansion, illustrated in Figure 1, but differs qualitatively and fundamentally, breaking the relation between geometry and destiny.
 |
 |
 |
|
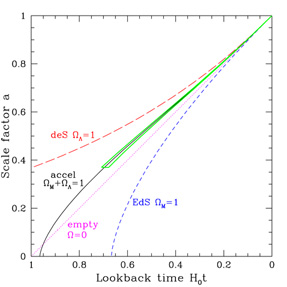
Figure 1. Mapping the expansion
history has
been a major theme of cosmology, revealing the constituents and nature
of our universe. From early models with diverse properties (top left
panel), scientists narrowed in to a region shown by the green box
corresponding to Big Bang models with a long matter dominated
epoch. By the 1980s cosmologists believed the universe corresponded to
an Einstein-de Sitter universe with critical matter density, or
perhaps some model more toward the empty universe curve (top right
panel). The remarkable discovery in 1998 of accelerated expansion
showed that the correct model must be similar to the solid black
curve, partaking of characteristics of the de Sitter universe with a
cosmological constant
|
|
For a non-accelerating universe described on large scales by a smooth, homogeneous and isotropic, i.e. Friedmann-Robertson-Walker model, geometry and destiny are inextricably linked. Whether the spatial curvature is positive, zero (flat), or negative correlates one-to-one with whether the expansion is closed (bounded), critical (asymptotically static), or open (unbounded). However, the Einstein field equations governing the cosmic expansion involve not only the amount of energy density but the full energy-momentum contribution. So there is a loophole to escape destiny.
The Friedmann equations (the Einstein equations in a homogeneous, isotropic model) can be written as
 |
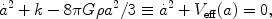(1) |
where a is the expansion scale factor, k is the spatial
curvature, and
is the
total energy density. (We consider the effective
potential Veff below.)
From the continuity (or conservation of energy-momentum) equation, the
total energy density
will evolve
with expansion as
~
a-3(1+w), where w = p /
is the
pressure to energy density, or
equation of state, ratio (easily generalized for a time varying ratio).
So
a2 ~ a-(1+3w).
If w > -1/3 then the sum of the k and
a2 terms
ranges from -
to
k for all values of a, i.e. the entire
expansion history. Thus, whether a2 ever reaches zero
and hence whether there is a maximum value of a or expansion
continues without halt is wholly governed by the value of the spatial
curvature k: is it positive or negative. Geometry controls density.
However, if w < -1/3 then the
a2 term grows with a and
eventually dominates as the expansion factor grows large. This strongly
negative contribution can overcome a positive k, so this breaks the
link between geometry and destiny.
One can get a visual appreciation for this by considering the k and
a2 terms together as making up an effective potential
energy (see, e.g.,
[5]),
such as standardly used in physics analysis
to determine whether a system with a certain kinetic energy is bound or
not. Here, the analog of kinetic energy is a2, and we
want to know whether the minimum kinetic energy, a2 =
0, hits the potential energy curve for any value of a, indicating
a maximum expansion factor.
Figure 2 for the effective potential
Veff vs. a
then illustrates the conditions discussed above. If w > -1/3
then the effective potential
ranges from - to
k for all values of a, i.e. the entire
expansion history. Thus, whether the effective potential crosses the
minimum kinetic energy value of zero
and hence whether there is a maximum value of a or expansion
continues without halt is wholly governed by the value of the spatial
curvature k: geometry controls density.
 |
Figure 2. Effective potentials for
universes classified according to their geometry (sign of k) and
whether the cosmic expansion accelerates (w < -1/3) or
not. Models crossing the dotted zero line do not expand
forever. For w > -1/3 the geometry determines the destiny:
whether models with physical kinetic energy, hence
Veff |
However, if w < -1/3 then the second term of the effective potential eventually dominates as the expansion factor grows large. This strongly negative contribution can overcome a positive k, so one can in fact have an eternal, positive curvature universe. Conversely, if the energy density itself goes negative (e.g. due to a negative cosmological constant) then a finite, negative curvature universe is possible. To determine the crucial quantity, the value of w, we need to take into account the entire energy-momentum not just the energy density. From the other Friedmann equation,
 |
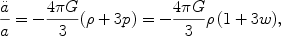(2) |
we see that the condition w < -1/3 is precisely the condition for accelerated expansion, a > 0. When one of the components of the universe has sufficiently negative pressure and contributes substantial energy density, such so-called dark energy can cause the total equation of state to drop below -1/3 and cause acceleration. Destiny then becomes unhinged from geometry, and we must understand the nature of dark energy to predict the fate of the universe. We discuss this further in Section 2.5.
Einstein's equivalence principle states that acceleration is curvature is gravity. While space may (or may not) be flat, spacetime curvature is nonzero in an expanding universe. Rather than viewing gravity as a force acting at a distance, we can view it as the curvature of spacetime and particles follow paths of least action (geodesics) in this curved spacetime. An intuitive way of seeing these deep connections is given in Figure 3.
 |
Figure 3. A photon experiences a frequency shift from acceleration, gravity, or spacetime curvature. Here the spacetime diagram illustrates a Pound-Rebka experiment of a photon propagating from one atom to another at height h above it. A gravitational field leads to a gravitational redshift z = gh / c2, while equivalently a uniform acceleration g over a time t leads to a velocity v = gt and a Doppler shift z = v / c = gt / c = gh / c2. Since a frequency change is equivalent to a change of time intervals, the horizontal, parallel line segments representing the emitted photon pulse period t0 and received period t' cannot be equal. This means the photon propagation lines (wavy diagonal lines), which should each be at 45° in a flat spacetime diagram, must not in fact be parallel. Thus acceleration, gravitation, and spacetime curvature are equivalent. |
Thus, mapping the expansion history and its acceleration is equivalent to mapping spacetime or to exploring the gravitational nature of the universe.
Is the discovery and further exploration of cosmic acceleration truly revolutionary? Let us ask what is our current understanding of the universe through the Standard Model: baryons, photons, neutrinos, etc. make up roughly 4% of the energy density of the universe. Understanding 4% is like one letter out of the alphabet, e.g. reading
The nature of the physics of the accelerating universe is the premier mystery for this generation of physics. The challenge of a new, dominant, strongly negative pressure component of the universe is closely tied with the foundations of quantum theory and the nature of the vacuum; it is central to the theory of gravitation and the nature of spacetime, possibly even the number of dimensions. The behavior of dark energy governs the fate of the universe.
We may hope to soon detect and eventually characterize dark matter. What will be our understanding once we have succeeded with this characterization and employed it to extend the Standard Model to a new theory of high energy physics such as supersymmetry? Then we will comprehend 25% of the energy density of the universe, like all the vowels (with y) of the alphabet:
The nature of the physics of the accelerating universe is the premier mystery for this generation of physics. The challenge of a new, dominant, strongly negative pressure component of the universe is closely tied with the foundations of quantum theory and the nature of the vacuum; it is central to the theory of gravitation and the nature of spacetime, possibly even the number of dimensions. The behavior of dark energy governs the fate of the universe.
It is apparent that for true understanding we will need to know the nature of dark energy. Only then will we have a complete and comprehensible picture:
The nature of the physics of the accelerating universe is the premier mystery for this generation of physics. The challenge of a new, dominant, strongly negative pressure component of the universe is closely tied with the foundations of quantum theory and the nature of the vacuum; it is central to the theory of gravitation and the nature of spacetime, possibly even the number of dimensions. The behavior of dark energy governs the fate of the universe.
Understanding cosmic acceleration undeniably will extend the frontiers of physics and rewrite the textbooks. It is not excessive to suggest that we are faced with a revolution in our understanding of nature as profound as the mystery of blackbody radiation a century ago. Blackbody radiation taught us the existence of photons and the structure of atoms; dark energy may lead us to the existence of quantum gravity and the structure of the vacuum.
. The challenge
now is to further improve
our cosmic mapping ability to zoom in on the narrow green triangular
region, revealing the nature of the new physics behind acceleration
(bottom panel). (See
[
0,
can achieve
a 