Bars are common features in disk galaxies. An earlier review (Sellwood & Wilkinson 1993) of the vast topic of bars is now somewhat dated but, as it provides a still useful summary of the basic dynamics, the present article will update a few main points and the reader is referred to the earlier review for a more detailed discussion.
For a long time, dynamicists were struggling to understand the absence of bars in some disk galaxies (Ostriker & Peebles 1973), but since reasonable models of luminous galaxies that include a dense bulge of moderate mass are now known to be stable (Section ), the problem has become almost the opposite! Strong bars are seen in many galaxies whose mass distributions now appear unfavorable to the dynamical bar instability, as evidenced by a nuclear gas ring (see Section 9.4), which can form only if the center is dense enough to have inhibited bar formation by Toomre's mechanism.
However, the fact that the center is dense today does not require that it was dense when the bar formed; secular inflow of gas (Section 9.4) can build up the central density after the bar has formed. Alternatively, the bar could have grown in size and slowed trhough disk evolution (Sellwood 1981, Berentzen et al. 2007) or halo friction (Athanassoula 2002, see Section 9.8), or have been triggered by large density fluctuations in the disk (Sellwood 1989a), by tidal interactions (Noguchi 1987, Berentzen et al. 2004, Curir et al. 2006), halo substructure (Romano-Díaz et al. 2008b) or a non-axisymmetric halo (Dubinski & Chakrabarty 2009). Any of these considerations, or that described in the next paragraph, could plausibly reconcile the existence of bars in these galaxies with Toomre's stabilizing mechanism.
In an elegant piece of dynamics,
Lynden-Bell (1979)
demonstrated that the
inner parts of galaxies are regions where eccentric orbits have a
tendency to align themselves, which allows a bar to grow slowly
through orbit trapping. The region where a cooperative response to a
mild perturbation occurs is where the overall radial density profile
of the galaxy flattens into a more uniform core. In this region, the
radial variation of 
- 
/ 2 has a maximum at
some non-zero
radius and an infinitesimal bar pattern can have a pattern speed that
allows two ILRs. Lynden-Bell's aligning mechanism, which operates
best on the more eccentric orbits, requires
p
-
R / 2 of
orbits in the aligning region. As this
pattern speed is much lower than that expected from the global bar
instability (Section 4.1), the aligning
mechanism offers an
additional route to bar formation in otherwise globally stable disks.
Although the cooperative region has a small radial extent,
Lynden-Bell (1979)
suspected the bar could be much larger.
Erwin (2005) presented a useful study of bar properties and pointed out that bars in late-type galaxies are often much smaller relative to the disk size than are those formed in sumulations.
Strong bars are clearly visible in 25% - 30% of disk galaxies (e.g.
Masters et
al. 2010),
and the fraction rises to
50% when more
objective criteria are applied to red or near-IR images
(Eskridge et
al. 2000,
Marinova & Jogee
2007,
Reese et al.
2007
and further references cited below).
Barazza et al.
(2008)
found a higher bar fraction in later Hubble types, while
Méndez-Abreu
et al. (2010)
found no bars in either very luminous, or very faint, galaxies.
Whatever may be the mechanism responsible for the formation of bars in real galaxies, none of the above suggestions makes a clear prediction for the frequency of bars. Bosma (1996), Courteau et al. (2003), and others have pointed out that barred galaxies seem little different from their unbarred cousins in most respects, e.g. they lie on the same Tully-Fisher relation. Minor systematic differences do exist: e.g. Davoust & Contini (2004) note that barred galaxies seem to have smaller mass fractions of neutral HI gas, but this seems more likely to be the result, rather than the cause, of the bar. The anti-correlation of bar frequency with the bulge half-light (Barazza et al. 2008) possibly results from Toomre's stabilizing mechanism, but this cannot be the whole story because some near-bulgeless disks are unbarred while other barred disks have massive bulges.
If no dynamical property, other than their eponymous one, can be identified that cleanly separates barred from unbarred galaxies, then the existence of a bar in a galaxy may possibly be determined by external factors, such as a chance encounter. Elmegreen et al. (1990) reported an increased fraction of bars in groups and clusters, but more recent work (Barazza et al. 2009, Li et al. 2009, Aguerri et al. 2009) has found little or no variation of bar fraction with environment. It is also possible that the bar fraction could be changing with time; different groups disagree (Jogee et al. 2004, Sheth et al. 2008), probably because observations of galaxies at significant look-back times are subject to systematic difficulties due to band-shifting and changing spatial resolution (see also Elmegreen et al. 2007).
A radical alternative is to regard bars as transient features that form and decay, and that the current fraction of barred galaxies represents the duty cycle (Bournaud et al. 2005). Bars in N-body simulations are dynamically rugged objects that appear to last indefinitely. Of course, they could be destroyed by a merger event, for example, although not much in the way of a cool disk would survive such an event. Norman and his co-workers (Pfenniger & Norman 1990, Norman et al. 1996) have argued that bars can be destroyed by the accumulation of mass at their centers, which may lead to a pseudo-bulge and/or a hot inner disk. However, Shen & Sellwood (2004) and Athanassoula et al. (2005) found that unreasonably large and/or dense mass concentrations were required to cause their bars to dissolve. The simulations by Bournaud et al. (2005) uniquely show that gas accretion may aid the dissolution of the bar and, with star formation, could recreate a cool disk that would be needed to make a new bar. Even if this behavior can be confirmed by others, the model requires very substantial gas infall. Moreover, the continued existence of the hot old disk and the build-up of a dense center makes every cycle of this speculative picture harder to achieve.
In the distant future, galaxy formation simulations (see chapter by Steinmetz) may have the quality and resolution perhaps to be able to predict the correct bar fraction, and thereby reveal their cause.
This section gives a brief description of a few important aspects of the orbital behavior in large-amplitude bars, and the reader is referred to Sellwood & Wilkinson (1993) for a more comprehensive discussion. Weak bars can be treated using epicycle theory (BT08, Section 3.3.3). Most early orbit studies in strongly barred potentials considered motion confined to the plane perpendicular to the rotation axis. Even though 3D motion is much richer, the fundamental structure of bars is most easily understood from in-plane orbits.
Since bars are believed to be steadily-rotating, long-lived objects,
it makes sense to discuss their structure in a frame that co-rotates
with the potential well at the angular rate
p. A rotating
frame has the effective potential
 |
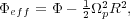(16) |
where 
is the potential
in an inertial frame.
The effective potential surface in the disk plane (eq. 16)
resembles a volcano, with a central crater, a rim, and a steeply
declining flank. The crater is elongated in the direction of the bar,
and the rim has four Lagrange points: two maxima,
L4 and
L5, on the bar minor axis and two saddle points,
L1 and L2 on
the bar major axis. (The fifth Lagrange point, L3, is
the local potential minimum at the bar center.) Because of Poisson's
equation, the density contours of the bar must be more elongated than
those of the inner
eff.
Neither E nor Lz is conserved in
non-axisymmetric potentials, but Jacobi's invariant IJ
(eq. 6) is conserved even for
strong bars that rotate steadily. Since IJ =
1/2|v|2 +
eff, where
v is the velocity in the rotating frame, contours of
eff bound the
possible trajectories of stars
having IJ less than that contour value. Stars that are
confined to the bar, which also have IJ <
eff(L1), are of most
interested here.
A periodic orbit is a possible path of a star in the rotating frame that retraces itself, usually after a single turn around the center, but always after a finite number of turns. Because the orbits close, the orbital period in the rotating frame is commensurable with the radial period and these orbits are also described as resonant orbits of the (strongly non-axisymmetric) potential.
Periodic orbits can be either stable, in which case a star nearby in phase space oscillates (librates) about its parent periodic orbit in an epicyclic fashion, or they are unstable, in which case the trajectory of a star nearby in phase space diverges exponentially (at first) from the periodic orbit. The orbits of stars that librate around a periodic orbit are known as regular orbits, those that diverge from it are known as irregular or chaotic orbits. Chaotic orbits have only a single integral, IJ, while regular orbits have an additional integral (two more in 3D) that confines their motion to a hypersurface of smaller dimension in phase space. Regular orbits are the more interesting because the star's orbit can be more elongated than the potential surface that confines it, which is of great value when building a self-consistent bar model.
The main features can be illustrated in the simple potential (cf. BT08, eq. 3.103)
 |
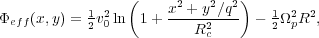(17) |
where R2 = x2 +
y2, Rc is a core radius inside of
which the potential is approximately harmonic,
q 
1 is the
flattening, and v0 is the circular speed at large
R when q = 1. As in BT08, the
values are: v0 = 1, q = 0.8,
Rc = 0.03, and
p = 1. With
these parameters, the major-axis Lagrange points lie at a distance
RL
0.9996 from the bar center.
The 2:1 resonant periodic orbits shown in Fig. 13 have a range of IJ values, but all close in the rotating frame after two radial oscillations for every turn about the center. Orbits of the main family, denoted x1, are elongated parallel to the bar (horizontal in the Figure), and are referred to as the backbone of the bar, since the majority are stable. Stars on these orbits all move in the same direction as the bar rotates, but have shorter periods because they are interior to the Lagrange points (or more loosely, they are inside CR). Some x1 orbits are simple closed figures, but others have loops near the outer ends where the star progresses around the center of the galaxy more slowly than does the rotating frame. Sparke & Sellwood (1987) and Voglis et al. (2007) found that a large fraction of particles in an N-body bar librate around them, and the same behavior is expected for stars in real bars.
 |
Figure 13. Examples of important periodic orbits in a rotating bar potential that close after two radial oscillations for every turn about the center, the 2:1 resonant families. Those orbits elongated parallel to the bar axis (horizontal) are members of the x1 family. The x2 orbits are elongated perpendicular to the bar. |
Another important family of 2:1 orbits appears near the center of the bar, but is elongated perpendicular to the bar axis, as also shown in Fig. 13. This family, denoted x2, is almost always stable and is present in many realistic bar potentials. Since Lindblad resonances (Section 2.4) are defined for infinitesimal perturbations to axisymmetric potentials, the label ILR is very loose usage in strong bars. It is true that the x2 family appears in barred potentials only, but not always, when the axisymmetric mass distribution and pattern speed admit one or more ILRs. Furthermore, x2 orbits orient themselves perpendicular, while the x1 family is parallel, to the bar axis, which is directly analogous to the abrupt phase shift that occurs in the response of a forced harmonic oscillator as the forcing frequency crosses its natural frequency (cf. Sanders & Huntley 1976). At finite amplitude, the near circular orbit sequence acquires gaps at the 2:1 resonance bifurcations, which become broader as the bar amplitude rises. Thus the radial extent of the x2 family shrinks as the strength of the bar is increased, and it may disappear entirely. Even if one is careful to say that the appearance of the x2 family is the generalization of the ILR to strong bars, the radius of this resonance is still badly defined because the orbits that appear inside it can be quite eccentric.
As IJ approaches the value of
eff(L1), the time to
complete a full turn in the rotating frame lengthens and additional
orbit families appear. Orbits that close after any number of radial
oscillations can be found in principle, but of these only the 4:1
resonant orbits are of dynamical significance to bar structure. As
the period lengthens, the proliferation of orbit families causes a
precipitous decrease in the stable regions around each parent and
chaotic behavior ensues
(Chirikov 1979).
The onset of chaos near CR led
Contopoulos (1980)
to expect the density of a self-consistent bar to
drop steeply near the major axis Lagrange points, leading to the rule
that the length of a bar is limited by CR. This rule predicts that
the parameter
(Elmegreen 1996)
 |
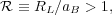(18) |
where aB is the semi-major axis of the bar. In principle,
self-consistent bar dynamics could allow bars with
>> 1,
although empirical bar pattern speed estimates
(Section 9.5) mostly
find that CR is in fact only slightly beyond the end of the bar.
There are many more in-plane orbit families, but few are of dynamical importance to the structure of the bar. See Sellwood & Wilkinson (1993) for a fuller account.
The extension to 3D allows for many more resonances between the in-plane motion and the vertical oscillations. While there is a rich variety of behavior (Pfenniger & Friedli 1991, Skokos et al. 2002), the backbone x1 family from 2D continues to be the most important, but now with a "tree" of orbits also librating vertically. The new periodic orbits that appear in 3D have a similar projected shapes as the in-plane x1 family, but they also librate vertically a small number of times over the same period as the motion in the plane. Patsis et al. (2002) highlighted the orbit families that they found to be of importance for the "boxy" appearance of edge-on bars (see also Section 9.7).
When pressure and magnetic forces can be neglected, any mild dissipation will drive gas to move on stable periodic orbits. An organized streaming gas flow pattern is expected wherever the simplest periodic orbits over a range of energies can be nested and intersect neither with neighboring orbits, nor with themselves. Shocks, where pressure ceases to be negligible, must occur in flows either where periodic orbits self-intersect, or where gas flows on two separate orbits cross. Fig. 13 shows that were gas to flow in that adopted bar potential, shocks would be inevitable because many orbits self-intersect (the loops) and, in particular, x2 orbits cross the x1 family. Thus shocks are a general feature of cool (low pressure) gas flows in bars. 14
Full hydrodynamic simulations (e.g. Roberts et al. 1979, Athanassoula 1992, Fux 1999) are needed to determine the flow pattern. Shocks are offset to the leading sides of the bar major-axis in models having reasonable parameters. Prendergast (1962) seems to have been the first to associate the dust lanes in bars with the locations of shocks in the gas.
Shocks convert some kinetic energy of bulk motion in the gas into heat, which is radiated efficiently. Furthermore, the offset location of the shock causes the gas to spend more than half its orbit on the leading sides of the bar, where it is attracted backwards towards the bar major axis, causing it to lose angular momentum. 15 Thus gas in the bar region must settle a little deeper into the potential well on each passage through a shock, i.e. the bar drives gas inwards, the angular momentum it loses being given to the bar.
The inflow stalls where gas settles onto the x2 orbit family, which is found in bar models that have dense centers, leading to a build up of gas. This behavior can be associated with nuclear rings of dense gas (Regan et al. 2002), which are often the sites of intense star formation also (Maoz et al. 2001, Benedict et al. 2002). If this were the whole story, the gas could not be driven any further inwards, but there is both observational evidence, in the form of spiral dust lanes and star formation (e.g. Carollo et al. 1998), and some theoretical work (Wada 2001) to suggest that self-gravity causes inflow to continue. However, the existence of high gas density and rapid star formation in the nuclear ring indicates that only a small fraction of the gas continues inwards.
Modeling the gas flow in a specific galaxy allows one to determine two
properties of the bar that are hard to constrain otherwise.
Estimating the gravitational potential of the galaxy from a
photometric image plus a dark halo,
Weiner et al.
(2001)
fitted for both the disk mass-to-light (M/L) and
p in the
galaxy NGC 4123. These
authors also described the procedure in detail. Results for a number
of other galaxies were reported by
Pérez et
al. (2004),
Weiner (2004),
and
Zánmar
Sánchez et al. (2008),
although these last authors were unable to obtain an
entirely satisfactory fit.
Lindblad et
al. (1996)
fixed the M/L and fitted only for
p. All
these fits preferred rapidly rotating bars in heavy disks.
Pérez (2008)
confirmed that the best fit parameters
of M/L and p
were the same for both 2D Eulerian (Godunov)
and 3D Lagrangian (SPH) hydrodynamic methods.
Even though the quadrupole field of a bar decays quickly with radius, it can be strong enough to drive a spiral shock in the gas of the outer disk, as originally demonstrated by Sanders & Huntley (1976). Schwarz (1981) showed that when gas is modeled as inelastic particles, it is driven outwards to form an outer ring (see review by Buta & Combes 1996). However, it is unclear that spirals in the outer disks of real barred galaxies are the responses to the bar, and they may owe more to self-excited structures than to bar driving (Section 7, Sellwood & Sparke 1988, Buta et al. 2009). In addition, the outer spiral response to an imposed bar is not steady in modern simulations, with the shapes of the driven arms cycling through a broad range. For these reasons, the gas flow models fitted to individual galaxies should rely primarily on the fit within the bar and pay little attention to the outer disk.
Kranz et al. (2003) tried a similar approach, but fitted a spiral pattern instead of a bar, which may yield unreliable results for two reasons: (i) The lifetimes of spiral arms are believed to be short (Section 7) leading to broader resonances and stronger gas responses than would arise in simulations that assume a slowly evolving pattern, and (ii) the observed spirals could be the superposition of several features with different angular rotation rates. As bars undoubtedly last for longer than do spirals and dominate the non-axisymmetric potential, fits to bars in galaxies are likely to yield better disk mass estimates.
Tremaine & Weinberg (1984a) devised a method to measure the pattern speed of a bar directly from observations of a tracer component, which must obey the equation of continuity. Their original method assumes that the galaxy has but a single pattern, and would yield a misleading result were there more than one pattern, each rotating at a different angular rate.
The stellar component of early-type barred galaxies is believed to
obey the equation of continuity because these galaxies have little
dust obscuration and no star formation. They also rarely possess
prominent spirals in the outer disk. Results of many studies using
this method for early-type barred galaxies were summarized by
Corsini (2008)
and are shown in Fig. 14. While some
individual measurements are quite uncertain, the data seem to favor 1
<
1.4.
Chemenin &
Hernandez (2009)
found a counter-example in a low-luminosity galaxy.
 |
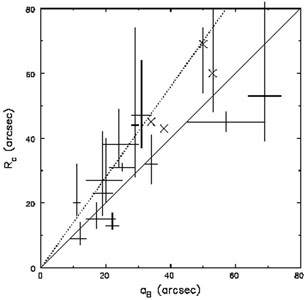Figure 14. Summary of direct pattern speed
measurements for bars collected by
Corsini (2008).
The diagonal line shows |
Fathi et al. (2009) and Meidt et al. (2009) applied the method of Tremaine & Weinberg (1984a) to ionized and molecular gas, respectively. Both groups argue that this is valid, even though the sperate gas components do not obey the continuity equation that undelies the method. Fathi et al. (2009) generally find fast bars. Meidt et al. (2008) generalized the method to attempt to measure radial variations in the pattern speed and Meidt et al. (2009) found suggestions of pattern speeds that are lower at large radii than those near the center.
Other methods can yield indirect estimates of bar pattern speeds.
Fits of models of the gas flow (Section 9.4) have
been reported for a few galaxies, finding
~ 1.2.
Athanassoula (1992)
argued that the shapes and locations of dust lanes in bars also seem
to suggest that
1.2. Associating a ring
in a barred galaxy with the location of a major resonance with the bar
(Buta & Combes
1996)
yields, with kinematic information, an estimate of the pattern speed.
Rautiainen et
al. (2008)
computed models of the stellar and gas (sticky particles)
responses to forcing by photometric models of 38 barred galaxies, in
which they assumed that the entire non-axisymmetric structure rotated at
the same pattern speed. They attempted to match the model to the visual
morphology of the galaxy, and found a range of values for
.
However, in most cases where
>> 1, the fit is
dominated by the outer spiral, which may have a lower angular speed than
does the bar.
Erwin & Sparke (2002) and others have found inner secondary bars within the inner parts of > 25% of large-scale or primary bars. They reported that the secondary bar has a length some ~ 12% of that of the primary bar and the deprojected angles between the principal axes of the two bars appeared to be randomly distributed, suggesting that the two bars may tumble at differing rates. This inference was supported by Corsini et al. (2003), who used the Tremaine & Weinberg (1984a) method to show that the two bars in NGC 2950 could not have the same rotation rates; Maciejewski (2006) used their data to argue that the secondary bar has a large retrograde pattern speed.
The theoretical challenge presented by these facts is substantial, and progress to understand the dynamics has been slow. Maciejewski & Sparke (2000) studied the orbital structure in a potential contain two nonaxisymmetric components rotating at differing rates. However, it is almost certain that the secondary bar can neither rotate at a uniform rate (Louis & Gerhard 1988) nor can it maintain the same shape at all relative phases to the primary.
Friedli & Martinet (1993) argued that gas was essential to forming secondary bars (see also e.g. Heller et al. 2001, Englmaier & Shlosman 2004). However, some of the collisionless simulations reported by Rautiainen & Salo (1999) and Rautiainen et al. (2002) manifested dynamically decoupled inner structures when the inner disk had high orbital frequencies due to a dense bulge. The structure was more spiral like in some models, but others appeared to show inner bars that rotated more rapidly than the main bar.
Debattista & Shen (2007) created long-lived, double-barred galaxy models in collisionless N-body simulations having dense inner disks, which they described as pseudo-bulges. They followed up with a more detailed study (Shen & Debattista 2009) that also made some predictions for observational tests. The secondary bars in their models indeed rotated at non-uniform rates, while their shape varied systematically with phase relative to that of the primary. These models prove that collisionless dynamics can support this behavior, but it is unclear that their initial conditions mimicked those that have given rise to double barred galaxies in nature.
The possible consequence of gas inflow in these galaxies has attracted a lot of attention. Shlosman et al. (1989) speculated that bars within bars might lead to gas inflow over a wide dynamic range of scales, from global to the parsec scale where accretion onto a black hole might cause AGN activity. While inflows may have been observed (e.g. Haan et al. 2009), understanding of gas flow in these non-steady potentials remains rather preliminary (Maciejewski et al. 2002, Heller et al. 2007).
Combes & Sanders (1981) first reported that the bars in their 3D simulations were thicker than the disk from which they had formed, and had acquired a pronounced "boxy" shape when viewed edge-on. Boxy isophotes in edge-on disk galaxies are now believed to be an indicator of a bar, as is supported by kinematic evidence in the gas (Merrifield & Kuijken 1999, Bureau & Athanassoula 2005).
The reason the bar thickened was explained by
Raha et al.
(1991),
who showed that bars are subject to the buckling instability
(Section 8.1).
The bar buckles because the formation of the bar created a structure
supported by elongated orbits that stream along the bar in the near
radial direction. Even though the ingoing and outgoing stars stream
on different sides of the bar, the effective averaged
R has
risen as a result without changing
z. The
simulation by
Raha et al.
(1991)
revealed that the buckling instability produced a large
amplitude arch just before it saturated, after which the bar became
thicker. The energy to increase vertical motion in the bar appeared
to have been released by the further concentration of mass towards the
bar center (see also
Martinez-Valpuesta
& Shlosman 2004).
It is delightful that the evolution of one instability, the bar-forming
mode, should create a new structure, the bar, that is itself unstable.
Bars still thicken in more recent simulations with grids having higher
spatial resolution (e.g.
Fig. 6), but do not seem to
exhibit the spectacular arch reported by
Raha et al.
(1991)
unless bi-symmetry is enforced. Low spatial resolution or significant
gravity softening (which are equivalent) weakens the restoring force
in eq. (13) and artificially increases
J, which is
the characteristic length for instability. Stronger gravity causes
the preferred buckling modes to have shorter wavelength allowing, say,
an upward arch on one side of the center and downward arch on the
other. Enforcing bi-symmetry prevents the bar from bending in this
anti-symmetric manner, and forces it to buckle through the single
arch mode.
9.8. Dynamical Friction on Bars
Friction between a rotating bar and a massive halo was first reported many years ago (Sellwood 1980), but the implications for dark matter halos have fueled a renewed intense study of the topic.
Dynamical friction (Chandrasekhar 1943) is the retarding force experienced by a massive perturber as it moves through a background sea of low-mass particles. It arises, even in a perfectly collisionless system, from the vector sum of the impulses the perturber receives from the particles as they are deflected by its gravitational field (see Appendix). Equivalently, friction can be viewed as the gravitational attraction on the perturber of the density excess, or wake, that develops behind it as it moves, as was nicely illustrated by Mulder (1983).
Chandrasekhar's formula (BT08, eq. 8.6) for the acceleration of a
perturber of mass M moving at speed vM through
a uniform background, density
, of
non-interacting particles having an
isotropic velocity distribution with a 1D rms velocity spread
, may be written as
 |
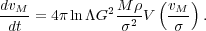(19) |
The Coulomb logarithm is defined in the Appendix, and the dimensionless function V is drawn in Fig. 15 for a Gaussian distribution of velocities; other velocity distributions would yield a different functional form. Physically, the retarding acceleration must vanish when the perturber is at rest and it must also tend to zero when the perturber moves so fast that the background particles receive only small impulses and the feeble wake lies far downstream from the perturber. Friction is strongest when the speed of the perturber is somewhat greater than the rms speeds of the background particles.
 |
Figure 15. The dimensionless acceleration function V defined in eq. (19) for the case of a Gaussian distribution of velocities among the background particles. The function is negative because the acceleration is directed oppositely to the velocity. |
The simplifying assumptions in its derivation invalidate application of eq. (19) to the physically more interesting problem of friction in a non-uniform medium in which the background particles are confined by a potential well and interact with the perturber repeatedly.
Repeated encounters between the perturber and thebackground particles require the more sophisticated treatment presented in Tremaine & Weinberg (1984b), who adopted a rotating potential perturbation in a gravitationally bound spherical halo of test particles. They showed, as did Lynden-Bell & Kalnajs (1972) for spiral waves, that lasting changes to the orbits of the halo particles appear to second order in the perturbing potential, and can occur only at resonances. They derived a daunting formula for the torque on the halo caused by the perturbation that sums the contributions from infinitely many resonances. The contribution at each resonance is proportional to the gradient of the DF near the phase-space location of the resonance, in a manner that is directly analogous to Landau damping. Weinberg (1985) computed the surprisingly large torque expected on a rotating bar, and his conclusion was confirmed in restricted tests (Little & Carlberg 1991, Hernquist & Weinberg 1992).
Weinberg & Katz (2007) pointed out that friction is dominated by a few important resonances. They estimated the widths of these resonances for a perturbation having constant pattern speed and finite amplitude, and argued that immense simulations would be needed to populate the resonance with sufficient particles to capture the correct net response. However, the loss of angular momentum from the perturber causes its pattern speed to change, and the resulting time-dependence of the forcing frequency is a much more important factor in broadening the resonances; thus friction can in fact be captured correctly in simulations having moderate numbers of particles (Sellwood 2008a). Note that the pattern speed of an orbiting satellite rises as it loses angular momentum, while that of a bar usually decreases.
Despite the complicated language of resonant dynamics, the upshot is simply that the perturber induces a wake-like response in the halo, as was beautifully illustrated by Weinberg & Katz (2007, their Fig. 1). As for the infinite medium, friction can be thought of more simply as the torque between the perturber and the induced halo response. Sellwood (2006, his Fig. 2b) shows the lag angle between the forcing bar and the halo response, which is about 45 when friction is a maximum and gradually decreases to zero as the bar slows, until eventually friction ceases when the halo response co-rotates with the bar.
Lin & Tremaine
(1983)
for an orbiting satellite, and
Sellwood (2006)
for a rotating bar, demonstrated that the frictional drag on the
perturbation scales with the mass of the perturber, M, the halo
density, ,
and the halo velocity dispersion,
exactly as
in eq. (19). Furthermore, the dimensionless function that
describes the dependence on the angular speed of the perturber shares
the general properties with V(x) that it is negative (for
reasonable non-rotating halos), and must
0 as x
, and that it should be
x as
x 0.
Including self-gravity in the halo response causes a further slight
increase in friction, but does not otherwise change the behavior.
9.8.2. Halo Density Constraint
Fully self-consistent simulations of bar formation in a live halo by Debattista & Sellwood (1998, 2000) showed that strong bars are indeed slowed rapidly. The fact that observed bars appear not to have been slowed (Section 9.5) may imply an upper bound to the density of the dark matter halo in barred disk galaxies. Valenzuela & Klypin (2003) claimed a counter-example of a bar that does not experience much friction in a "cosmologically-motivated" halo, even though their result disagreed with all others for strong bars (O'Neill & Dubinski 2003, Athanassoula 2003) and with theory!
Investigation of their anomalous result by Sellwood & Debattista (2006) revealed that friction can be avoided temporarily if the gradient of the DF at the most important resonance(s) has been flattened by earlier evolution, which they described as a metastable state. Lin & Tremaine (1983) reported similar behavior as a result of driving the perturber at constant frequency for a protracted period. They showed, as did Sellwood & Debattista (2006) and Villa-Vargas et al. (2009), that the full frictional drag resumes after some delay, the duration of which seems to vary stochastically (Sellwood & Debattista 2009). Delayed friction can happen only in simulations of disks in isolated, smooth halos, since any reasonable amount of halo substructure, or a tidal encounter, disturbs the delicate metastable state of the halo, causing friction to appear with its full force. Thus simulations that do not find strong friction from moderately dense halos (e.g. Klypin et al. 2009) have simply not been run for long enough.
While Debattista & Sellwood (2000) argued for near maximal disks, and their requirement for a low halo density is in agreement with the disk masses derived from fitting bar flow models (Section 9.4), their constraint on the halo density may be specific to their adopted halo models. Thus additional careful studies of other halo models seem warranted.
9.8.3. Halo Density Reduction by Bars
While a full discussion of processess that may lower the dark matter density in the centers of halos is outside this review, a brief mention of the effect of bar friction is appriate here.
Weinberg & Katz (2002) argued that the transfer of angular momentum from the bar to the halo could reduce the central density of the dark matter halo by a substantial factor. However, the possible density reduction is quite modest (Holley-Bockelmann et al. 2005, McMillan & Dehnen 2005, Sellwood 2008a) because the disk has only a finite amount angular momentum to give to the halo. Furthermore, as the disk loses angular momentum, its mass distribution contracts, and the deepening potential well further compresses the halo, which actually overwhelms the slight density reduction (Sellwood 2003, Colín et al. 2006).
14 Shocks may be avoided when pressure is significant (Englmaier & Gerhard 1997). Back.
15 The opposite happens in shocks outside CR, where the gas gains angular momentum from the bar. Back.