


The optically visible parts of galactic disks are usually remarkably thin and flat, whereas the more extended HI disks of many edge-on galaxies appear noticeably warped with an integral sign shape. Stellar warps (Reshetnikov et al. 2002, Saha et al. 2009) are much less pronounced than the warps in the extended gaseous disks. The long-known warp in the HI layer of the Milky Way (Oort et al. 1958) has been most recently analyzed by Levine et al. (2006), while the dust and stars of the outer disk appear to be distorted in a similar, though less extensive, shape (Reylé et al. 2009). Both gaseous and stellar warps are frequently asymmetric, as appears to be the case for the Milky Way. The fact that stellar warps usually follow the same warped surface as do the gaseous ones (see also Cox et al. 1996), is strong evidence that warps are principally a gravitational phenomenon.
Warps are extremely common. HI observations of edge-on galaxies (Bosma 1991, García-Ruiz et al. 2002b) find very high fractions of warps, and the true fraction must be even higher, since warps directed close to our line of sight may be missed. Warps can also be detected kinematically even when the system is not edge-on. Their ubiquity suggests that warps are either repeatedly regenerated or long-lived.
Briggs (1990) studied a sample of 12 warped galaxies with high-quality 21-cm data, and found that galactic warps obey three fairly simple rules:
Kahn & Woltjer (1959) first drew attention to the winding problem presented by warps (see also BT08, Section 6.6.1), and argued that while self-gravity would slow the differential precession, it could not be strong enough to create a long-lived warp. Lynden-Bell (1965), on the other hand, suggested that warps could result from a persisting misalignment between the spin axis and the disk normal, i.e. a long-lived mode.
This section describes the theory of bending waves in general before addressing warps more directly. Unstable bending modes will be denoted buckling modes, although other names that come from plasma physics, such as hose, firehose, or hosepipe instabilities, are commonly used.
8.1. Local Theory of Bending Waves
Toomre (1966)
considered the bending stability of an infinite, thin
slab of stars having a velocity dispersion
 x in the
x-direction and some characteristic thickness
z0. The
self-gravity of the slab causes it to bend coherently provided the
vertical oscillations of stars are adiabatically invariant as they
move over the bend, which requires the slab to be thin compared with
the wavelength of the bend. Furthermore, if the bending amplitude is
small, its effect on the horizontal motion is negligible.
x in the
x-direction and some characteristic thickness
z0. The
self-gravity of the slab causes it to bend coherently provided the
vertical oscillations of stars are adiabatically invariant as they
move over the bend, which requires the slab to be thin compared with
the wavelength of the bend. Furthermore, if the bending amplitude is
small, its effect on the horizontal motion is negligible.
Toomre derived the dispersion relation for small-amplitude,
long-wave (kz0 << 1) distortions of the
formh(x,t) = H
ei(kx -  t):
t):
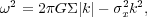 |
(13) |
where  is the
vertically-integrated surface density of the
slab. The first term on the RHS is the restoring force from
the perturbed gravity caused by the bend, while the second is the
inertia term due to the vertical acceleration needed for stars to
follow the corrugations. The inertia term is destabilizing and
outweighs the gravitational restoring force when
is the
vertically-integrated surface density of the
slab. The first term on the RHS is the restoring force from
the perturbed gravity caused by the bend, while the second is the
inertia term due to the vertical acceleration needed for stars to
follow the corrugations. The inertia term is destabilizing and
outweighs the gravitational restoring force when
 <
<
 J =
J =
 x2 /
G
x2 /
G , causing
the distortion to grow
exponentially. The unstable range of the buckling instability is
precisely complementary to that of the Jeans instability in the plane
in the absence of rotation, which is unstable for wavelengths
, causing
the distortion to grow
exponentially. The unstable range of the buckling instability is
precisely complementary to that of the Jeans instability in the plane
in the absence of rotation, which is unstable for wavelengths
 >
>  J
(Toomre 1966).
J
(Toomre 1966).
The dispersion relation (13) predicts a buckling instability,
at sufficiently short wavelengths, for any razor-thin system.
However, it does not hold for wavelengths shorter than or comparable
to the actual vertical thickness of the slab. Since z0 ~
 z2 /
(G
z2 /
(G ), where
), where
 z is the
vertical velocity dispersion, one expects that bending at all
wavelengths will be suppressed when
z is the
vertical velocity dispersion, one expects that bending at all
wavelengths will be suppressed when
 z /
z /
 x exceeds
some critical value, which
Toomre (1966)
estimated to be 0.30. 12
x exceeds
some critical value, which
Toomre (1966)
estimated to be 0.30. 12
Araki (1985)
carried through a linear normal mode analysis of the infinite,
isothermal slab
(Spitzer 1942,
Camm 1950),
which has the
properties  =
=  0
sech2(z / 2z0), z0 =
0
sech2(z / 2z0), z0 =
 z2 /
(2
z2 /
(2 G
G
 ), and
), and
 =
4
=
4 0
z0. He assumed a
Gaussian distribution of x-velocities, with
0
z0. He assumed a
Gaussian distribution of x-velocities, with
 x
x

 z, and
determined the range of unstable wavelengths as the
slab was made thicker. He showed that the buckling instability could
be avoided at all wavelengths when
z, and
determined the range of unstable wavelengths as the
slab was made thicker. He showed that the buckling instability could
be avoided at all wavelengths when
 z > 0.293
z > 0.293
 x, in good
agreement with Toomre's earlier estimate. At the marginal stability
threshold, the last unstable mode has a wavelength
x, in good
agreement with Toomre's earlier estimate. At the marginal stability
threshold, the last unstable mode has a wavelength
 1.2
1.2
 J.
J.
Galaxy disks are not, of course, infinite slabs subject to plane-wave
distortions, but the radial velocity dispersion,
 R, which is
larger than the azimuthal dispersion, could perhaps be great enough to
drive a buckling instability. As the observed ratio of velocity
dispersions for stars in the Solar neighborhood is
R, which is
larger than the azimuthal dispersion, could perhaps be great enough to
drive a buckling instability. As the observed ratio of velocity
dispersions for stars in the Solar neighborhood is
 z /
z /
 R ~ 0.6
(Nordström
et al. 2004),
Toomre (1966)
concluded that at least this
region of our Galaxy is "apparently well clear of this stability
boundary." It should be noted that the approximate solution for the
potential, which requires kR >> 1, is stretched in this
case, since
R ~ 0.6
(Nordström
et al. 2004),
Toomre (1966)
concluded that at least this
region of our Galaxy is "apparently well clear of this stability
boundary." It should be noted that the approximate solution for the
potential, which requires kR >> 1, is stretched in this
case, since  J
J
 7 kpc when
7 kpc when
 R = 40 km
s-1 and
R = 40 km
s-1 and
 = 50
M
= 50
M pc-2.
pc-2.
When the disk is embedded in some external potential, arising from a halo or the distant bulge of the galaxy say, the dispersion relation for short-wavelength waves in a thin slab (13) acquires an additional stabilizing term
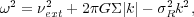 |
(14) |
where  ext2 =
|
ext2 =
| 2
2
 ext /
ext /
 z2|z = 0 (BT08 eq. 6.114). Taking
this additional factor into account further reinforces local stability
and global, axisymmetric simulations
(Sellwood 1996a)
confirmed that Toomre's conclusion holds everywhere in an axisymmetric,
but otherwise plausible, model of the Milky Way disk.
z2|z = 0 (BT08 eq. 6.114). Taking
this additional factor into account further reinforces local stability
and global, axisymmetric simulations
(Sellwood 1996a)
confirmed that Toomre's conclusion holds everywhere in an axisymmetric,
but otherwise plausible, model of the Milky Way disk.
As for WKB spiral waves (Section 3.2),
the dispersion relation
(14) can be generalized to tightly-wrapped
non-axisymmetric bending waves simply by replacing
 with
with
 -
m
-
m ,
with the angular rate of precession of the
bending wave that has m-fold rotational symmetry being
,
with the angular rate of precession of the
bending wave that has m-fold rotational symmetry being
 p =
p =
 / m.
It should be borne in mind that since observed warps in galaxies are
very far from being tightly wound, analyses that make this
approximation yield results that are at best only indicative of the
dynamical behavior.
/ m.
It should be borne in mind that since observed warps in galaxies are
very far from being tightly wound, analyses that make this
approximation yield results that are at best only indicative of the
dynamical behavior.
Vertical resonances between the bending wave and the stars arise where
m( p -
p -
 ) =
±
) =
±  (Section 2.6),
although the meaning
of
(Section 2.6),
although the meaning
of  here depends on the
context. BT08 (Section 6.6.1) considered
only razor thin disks, for which the internal oscillation frequency
here depends on the
context. BT08 (Section 6.6.1) considered
only razor thin disks, for which the internal oscillation frequency
 int is infinite and
the resonances occur where
m(
int is infinite and
the resonances occur where
m( p
-
p
-  ) = ±
) = ±
 ext. In disks of
finite thickness, the stars have a natural internal vertical frequency
ext. In disks of
finite thickness, the stars have a natural internal vertical frequency
 int2
int2
 4
4 G
G 0 (exact in the mid-plane of an infinite
slab), and for vertical resonances the appropriate value of
0 (exact in the mid-plane of an infinite
slab), and for vertical resonances the appropriate value of
 =
(
=
( int2 +
int2 +
 ext2)1/2. Henceforth,
ext2)1/2. Henceforth,
 will be
used to mean either this total frequency in a thickened layer or
will be
used to mean either this total frequency in a thickened layer or
 ext for a
razor-thin sheet.
ext for a
razor-thin sheet.
Eq. (14) is satisfied for both ±
m( p
-
p
-  ),
implying two possible pattern speeds known as fast and slow
waves. Because the gravity term raises the Doppler-shifted frequency
above
),
implying two possible pattern speeds known as fast and slow
waves. Because the gravity term raises the Doppler-shifted frequency
above  , waves in a cold disk
(
, waves in a cold disk
( R = 0)
extend away
from the vertical resonances, and do not exist in the region between
them that includes CR. The slow wave, which is a retrograde pattern for
m = 1, is of most interest because the unforced precession rate,
R = 0)
extend away
from the vertical resonances, and do not exist in the region between
them that includes CR. The slow wave, which is a retrograde pattern for
m = 1, is of most interest because the unforced precession rate,
 p =
p =
 -
-
 , has much the milder radial
variation.
, has much the milder radial
variation.
Much like density waves, neutrally-stable bending waves propagate in a disk in the radial direction at the group velocity (Toomre 1983)
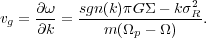 |
(15) |
Since the denominator is negative for slow bending waves, trailing
waves (k > 0) in a cold disk
( R = 0)
propagate inwards, while leading waves (k < 0) propagate
outwards. As for waves in non-uniform
whips, the bending amplitude rises when the wave propagates into a
region of lower surface density, and vice versa.
R = 0)
propagate inwards, while leading waves (k < 0) propagate
outwards. As for waves in non-uniform
whips, the bending amplitude rises when the wave propagates into a
region of lower surface density, and vice versa.
Unfortunately, a full description of wave propagation in a sheet of
finite thickness requires a solution of the linearized Boltzmann and
Poisson equations
(Toomre 1966,
Araki 1985,
Weinberg 1991,
Toomre 1995).
The results are not analytic and surprisingly more complex than equation
(14) for the razor-thin case. Because the vertical potential
of the disk is anharmonic, stars whose vertical oscillation takes them
far from the mid-plane have lower vertical frequencies. Thus, any
Doppler-shifted frequency
m( p -
p -
 ) of the bending wave
will be in resonance with some stars that will damp the wave by
converting wave energy into increased random motion. In general,
short-wavelength modes kz0
) of the bending wave
will be in resonance with some stars that will damp the wave by
converting wave energy into increased random motion. In general,
short-wavelength modes kz0
 0.5 damp in less
than one wavelength
(Weinberg 1991,
Toomre 1995),
while long-wavelength modes
kz0 << 1 can propagate large distances.
0.5 damp in less
than one wavelength
(Weinberg 1991,
Toomre 1995),
while long-wavelength modes
kz0 << 1 can propagate large distances.
Sellwood et al. (1998) studied the propagation anddamping of axisymmetric bending waves in disks having both finite thickness and non-zero random velocities.Waves launched from the center of the disk at a fixed frequency propagated outwards and were damped as they approached the vertical resonance. As a result the disk thickened over a small radial range, with the peak occurring just interior to the resonance.
Because of the complication caused by finite thickness, analytic work
almost always adopts the razor-thin approximation, which also requires
 R = 0, since
thin disks with velocity dispersion are
buckling unstable. 13
With these assumptions, the disk
can be approximated by a finite number of gravitationally coupled
circular rings of matter, each having the appropriate angular
momentum, which always admits a discrete spectrum of bending modes.
The real modes of the continuum disk can be distinguished by showing
they are independent of the number of rings employed.
R = 0, since
thin disks with velocity dispersion are
buckling unstable. 13
With these assumptions, the disk
can be approximated by a finite number of gravitationally coupled
circular rings of matter, each having the appropriate angular
momentum, which always admits a discrete spectrum of bending modes.
The real modes of the continuum disk can be distinguished by showing
they are independent of the number of rings employed.
The gravitational restoring forces are correctly captured in this approach, but the lack of random motion omits the additional coupling between adjacent mass elements caused by the epicyclic motions of the stars. This extra mechanism further stiffens the disk's resistance to bending (Debattista & Sellwood 1999), especially in the high density inner regions where radial epicycles are larger.
Hunter & Toomre
(1969)
developed the coupled ring approach to study the
bending dynamics of rotationally-supported, razor-thin disks with no
random motion and no halo. They were able to prove that general disks
of this kind have no axisymmetric (m = 0) or warping (m = 1)
instabilities, but they could not extend their proofs to higher
sectoral harmonics. In fact they noted that were the disk composed of
two equal counter-rotating populations of stars (on circular orbits)
it would be buckling unstable for all m
 2.
2.
Hunter & Toomre (1969) also studied the particular case of the sharp-edged Maclaurin disk in which all stars orbit at the same angular rate. When the sense of rotation is the same for all stars, the disk is stable to all bending waves, and there is a simple set of discrete neutral modes for all m. Polyachenko (1977) extended their analysis to Maclaurin disks with random motion (the Kalnajs disks) and was able to solve for the complete spectrum of bending modes. Needless to say, the introduction of random velocities in this razor-thin system caused buckling instabilities to appear for all m.
Since the Maclaurin disk bears little resemblance to real galaxies, Hunter & Toomre (1969) modified the disk to blur the sharp edge. They demonstrated that discrete warp modes in a cold, razor-thin disk can exist only when the edge is unrealistically sharp. Note that all isolated disks admit two trivial zero-frequency modes: a vertical displacement of the entire disk and a tilt of the disk plane to its original direction. More interesting standing wave solutions (modes) require traveling waves to reflect off the disk edge, but a realistic disk with a fuzzy edge does not reflect bending waves, because the group velocity decreases with the disk surface density (eq. 15) and a wave packet in a cold disk will never reach the edge (Toomre 1983).
8.3. Simulations of Buckling Modes
Sellwood & Merritt (1994) used N-body simulations to study the global instabilities of hot disks with no net rotation, i.e. with half the particles counter-rotating. (See Section 9.7 for buckling modes of more normal disks with large net rotation.) The form and vigor of the principal instabilities in any one of their models varied with the balance between radial and azimuthal pressure and with disk thickness: an in-plane lop-sided instability was the most disruptive for cool models (Section 5). The radially hotter thin disks were disrupted by axisymmetric bending instabilities (bell modes), as illustrated in Fig. 11. The instability creates a thick inner disk resembling a pseudo-bulge (see chapter by Kormendy). Very thin disks also buckled in an m = 2 "saddle" mode, and an m = 1 warp instability was detectable in some models, but never dominant.
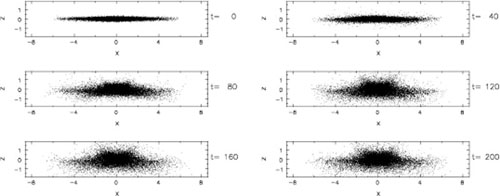 |
Figure 11. The development of a buckling instability in a simple model of an isolated stellar disk with Q ~ 2. The disk is KT/4 model described by Sellwood & Merritt (1994), with equal numbers of particles orbiting in each direction, but here the simulation uses a code of much higher spatial resolution. The buckling mode is axisymmetric and, while non-axisymmetric features were permitted by the code, none developed. The disk mass and radial scale are unity, and G = 1; the orbit period at R = 2 is 16 in these units. |
Remarkably, instabilities in a counter-streaming model having intermediate radial pressure caused rather mild changes and led to an apparently stable, moderately thin, and almost axisymmetric disk. The in-plane velocities in this model resemble those reported by Rubin et al. (1992) for the S0 galaxy NGC 4550, and indicate this galaxy could be stable even without large quantities of dark matter. The stability of this end product also demonstrated that thin axisymmetric systems with modest radial pressure are more stable to bending modes than those having isotropic or radially biased DFs.
Merritt & Sellwood
(1994)
proposed a criterion for the stability of a stellar system
to buckling modes that can be applied globally. A particle moving at
speed 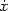 in a mildly bent
sheet with characteristic wavenumber
k experiences a periodic vertical forcing at frequency k
in a mildly bent
sheet with characteristic wavenumber
k experiences a periodic vertical forcing at frequency k
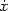 and, like any harmonic
oscillator, the phase of its response depends upon whether the forcing
frequency is greater or less than its natural vertical frequency. If
k
and, like any harmonic
oscillator, the phase of its response depends upon whether the forcing
frequency is greater or less than its natural vertical frequency. If
k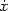 <
<
 , the density response of the
system to an imposed perturbation will be supportive, and the
disturbance can be sustained or even grow. However, if
k
, the density response of the
system to an imposed perturbation will be supportive, and the
disturbance can be sustained or even grow. However, if
k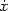 >
>  for most particles, the overall density response to the perturbation
will produce a potential opposite to that imposed and the disturbance
will be damped. They showed that their proposal successfully
accounted for their N-body results, for the behavior of the infinite
slab at short wavelengths, and for the apparent absence of elliptical
galaxies more flattened than E7.
for most particles, the overall density response to the perturbation
will produce a potential opposite to that imposed and the disturbance
will be damped. They showed that their proposal successfully
accounted for their N-body results, for the behavior of the infinite
slab at short wavelengths, and for the apparent absence of elliptical
galaxies more flattened than E7.
Sellwood (1996b) found a long-lived bending oscillation in an N-body simulation of a warm disk that was constrained to be axisymmetric. Apparently the system was able to support a standing wave, at most mildly damped, between the center and the edge of the disk, even though the stars had random motion in a disk of finite thickness. The frequency of the bending or flapping mode was low enough to avoid vertical resonances with almost all disk particles, in agreement with the requirement stated by Mathur (1990). While this result remains an isolated curiosity, since the flapping mode would probably be quickly damped in a halo, it is a clear counter-example to the argument by Hunter & Toomre (1969) that realistic disks do not possess global bending modes, which apparently holds only for disks without random motion.
Since the paper by Hunter & Toomre (1969), ideas of warp formation have relied in some way on the interaction between the disk and its dark matter halo. Dekel & Shlosman (1983) and Toomre (1983) suggested that a flattened halo misaligned with the disk could form a long-lasting warp. Sparke & Casertano (1988) and Kuijken (1991) obtained long-lived warps (dubbed modified tilt modes) of disks in rigid, misaligned halos, which were insensitive to the details of the disk edge. Lovelace (1998) studied the tilting dynamics of a set of rings also in a rigid halo, but assumed that the inner disk lay in the symmetry plane of the spheroidal halo.
Dubinski & Chakrabarty (2009) noted that the dark matter halos that result from cosmic structure formation simulations are usually aspherical, with frequent misalignments between the principal axes of the inner and outer halo. The disks in their simulations warped nicely when forced with slowly rotating, but otherwise rigid, perturbing fields representative of such halos.
However, dark matter halos are not rigid, and a responsive halo alters the dynamics in several ways. Nelson & Tremaine (1995) showed that were the inner disk misaligned with the principal plane of the flattened halo, as supposed by Sparke & Casertano (1988), its precession would be damped through dynamical friction, bringing the disk into alignment with the halo on time scales much shorter than a Hubble time. But a more compelling objection to the modified tilt mode emerged from N-body simulations with live halos: Dubinski & Kuijken (1995) found that the warp did not survive while Binney et al. (1998) showed that the inner halo quickly aligns itself with the disk, not vice versa. The large store of angular momentum in the disk maintains its spin axis, but the pressure supported inner halo can readily adjust its shape slightly to align itself with the disk.
The idea that galaxy warps are manifestations of eternal warp modes seems doomed by the damping effect of a live halo. But slowly evolving warps remain viable, provided that suitable external perturbations occur in enough cases.
In hierarchical galaxy formation scenarios, late infalling material
probably has an angular momentum axis misaligned with the disk spin
axis.
Ostriker & Binney
(1989)
therefore proposed that warps arise due to the
slewing of the galactic potential as material with misaligned angular
momentum is accreted. Structure formation simulations by
Quinn & Binney
(1992)
confirmed that the mean spin axis of a galaxy must slew as late
arriving material rains down on the early disk. The
less-than-critical matter density in modern
 CDM universe
models implies that infall is less pervasive at later times, but it
manifestly continues to the present day in gravitationally bound
environments
(Sancisi et
al. 2008,
and chapter by van Woerden & Bakker).
CDM universe
models implies that infall is less pervasive at later times, but it
manifestly continues to the present day in gravitationally bound
environments
(Sancisi et
al. 2008,
and chapter by van Woerden & Bakker).
Jiang & Binney (1999) and Shen & Sellwood (2006) presented results of experiments in which a disk was subjected to the torque from a misaligned, massive torus at a large radius. This well-defined perturbation is a very crude model of an outer halo that is rotationally flattened, and having its spin axis misaligned with that of the disk. It is misaligned and farther out because, in hierarchical scenarios, the mean angular momentum of the later arriving outer halo is probably greater and misaligned from that of the original inner halo and disk. The accretion axis is, in reality, likely to slew continuously over time, so a model with a constant inclination is somewhat unrealistic.
Rather than striving for realism, Shen & Sellwood (2006) used this simple forcing to reach an understanding of how the warp develops and why the LoN usually forms a loosely-wound, leading spiral. The inner disk maintained a coherent plane because of both self-gravity and random motion. The torque arising from the misaligned outer torus caused the inner disk, and the aligned inner halo, to precess rigidly even though the torque increased with radius, but the outer disk beyond ~ 4Rd started to warp.
As soon as the outer disk became misaligned with the inner disk, the strongest torque on the outer parts of the disk arose from the inner disk. The torque from the interior mass was responsible for the leading spiral of the line of nodes, even though the adopted external field would have produced a trailing spiral. The fact that the LoN of most warps forms a leading spiral over an extended radial range seems to imply massive disks.
Even though the disk precessed due to the externaltorque, its motion was barely damped over many Gyr, in contrast to the expectations from Nelson & Tremaine (1995). Damping was weak because the slow precession rate allowed the inner halo to remain closely aligned with the disk, which therefore caused little drag. The weak damping seemed to be caused more by the relative precession of the inner and outer parts of the halo. Also the warp evolved slowly as the layer settled to the main plane at gradually increasing radii, in apparent agreement with the decreasing outward group velocity.
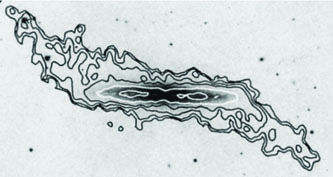
Fig. 12 shows the HI observation of NGC 4013 by Bottema (1996), together with the warp obtained in the simulation by Shen & Sellwood (2006). Their simulations revealed that the warp persisted for cosmologically interesting times, even when the external forcing field was removed. Thus the persistence of warps is not nearly as perplexing as previous studies had suggested. Furthermore, the model had a flat inner disk and the warp in the outer disk matched all of Briggs's rules quite well.
 |
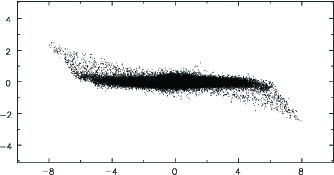 |
Figure 12. The upper panel shows the observed HI warp of NGC 4013 (Bottema 1996), and the lower panel the warp in the simulation by Shen & Sellwood (2006) that closely resembles it. The length unit on the axes is the scale length Rd of the exponential disc. |
A fixed outer torus is clearly unrealistic and the halo axis probably shifts continuously or episodically, as argued by Quinn & Binney (1992), making warp lifetimes a side issue. Warps formed this way can be repeatedly regenerated when a new infall event happens. Since cosmic infall and mergers are more likely to happen in a denser environment, warps can be induced more frequently in such an environment, which is consistent with the statistics (García-Ruiz et al. 2002b).
Tidal interactions between galaxies could be an additional cause of warps in disks, and one that is quite likely to produce asymmetrical warps. This idea has been explored most fully to explain the warp of the Milky Way's (MW) disk that results from the proximity of the Magellanic Clouds, especially the Large Cloud (LMC). The orientation of the principal axes of the warp (Levine et al. 2006) at least seems favorable to this hypothesis. Bailin (2003) suggested that the Sagittarius dwarf galaxy is another possible culprit.
Hunter & Toomre (1969), in models that did not include dark matter, concluded that the LMC could be responsible for the warp of the MW, but only if it was a lot more massive than was then suspected and had recently passed close to the edge of the disk. García-Ruiz et al. (2002a) tested the hypothesis in fully self-consistent simulations that included live halos and used updated information about the distance and motion of the LMC. They concluded that neither the amplitude, nor the orientation, of the warp in the disk of the MW was consistent with the tidal hypothesis. Weinberg & Blitz (2006), on the other hand, suggested that a co-operative response from the halo to the passage of the LMC could have generated the observed warp in the disk. Thus there is no consensus yet on the origin of the warp in the Milky Way.
12 Kulsrud et al. (1971) and Fridman & Polyachenko (1984) considered the bending instability in a constant density slab of stars with sharp edges. Back.
13 A razor thin disk is not destabilized by orbital motions with no velocity spread. Back.