3. GALAXY DIAGNOSTICS

In this and in the following section, we focus on objects for which a galaxy classification (or lack thereof) tends to be ambiguous.

3.1. Stellar kinematics

The most direct way to determine whether an object contains dark matter, or whether its properties are otherwise inconsistent with Newtonian gravity, is to conduct a kinematic study. The present day mass of a system is typically derived from its kinematics using formalism based on Newton's laws of gravity and the assumption of dynamical equilibrium. This dynamical mass can then be compared with the total mass present in the form of stars, stellar remnants, and gas. If dynamical mass exceeds the baryonic mass, then dark matter must be present or one of the dynamical assumptions - such as Newtonian gravity or virial equilibrium - must be flawed.

There are many regimes in which dynamical studies can be translated with few assumptions into Newtonian masses (e.g., Walker et al. 2009a; Wolf et al. 2010). Wolf et al. (2010) showed that the half-light mass of a dispersion supported system could be robustly calculated with only mild assumptions about the orbital anisotropy of its constituent stars. They derive M_half = 4G^-1 < _los² > r_half. Here M_half is the total mass within the 3D deprojected half-light radius, <_los²> is the luminosity weighted square of the line of sight velocity dispersion, and r_half is the 2D projected half-light radius. Such calculations have yielded (M / L)_half as high as ~ 3000 for a MW satellite galaxy (Segue 1, Simon et al. 2011).

It is not always possible to diagnose a galaxy definition based on dynamical (M / L)_half alone. Many authors have looked at the relationship between M / L and other system properties (such as luminosity, see e.g. Figures 3 and 5 in Tollerud et al. 2011 and Figure 4 in Wolf et al. 2010.) While typical star clusters stand out as having low (M / L)_half (~ 1-5) for their luminosities (L ~ 10^4-6 L), dispersion supported galaxies (L ~ 10^8-10 L) have similar (M / L)_half as star clusters. In such cases, a combination of (M / L)_half and other population arguments may be used to diagnose a galaxy classification (see also Section 3.3). Alternatively, dynamical modeling including tracers at larger distances can reveal M / L outside of r_half.

If the existence of dark matter is the correct interpretation of galaxy dynamics, then dynamical classification of galaxies may be robust to the effect of tidal mass loss. Simulations show that galaxies tidally stripped of mass should maintain a high dynamical mass-to-light ratio. For example, Peñarrubia et al. (2008) showed that the mass-to-light ratios of tidally evolving dwarf galaxies increase over time, assuming they reside in cuspy dark matter halos. Even if the dark matter halos hosting dwarf galaxies are cored, their central dark matter density slopes remain constant during tidal evolution (Peñarrubia et al. 2010).

3.1.1. Special Considerations

Generally, dynamical M / L 5 may be taken to diagnose a galaxy classification, because such M / L are larger than expected from typical stellar populations. However, a number of challenges face attempts to determine whether an observed dynamical M / L of a system is consistent with expectations from baryons alone - especially for systems with M / L 10, low intrinsic velocity dispersions, or low surface brightness. Some of these challenges are fairly obvious, as the dynamical M / L expected for a purely baryonic population varies significantly with: age, metallicity, initial mass function, dynamical state, and gas content. In this section, we highlight several specific examples which are less commonly discussed in the literature. See also Section 4.2.1 for a more nuanced discussion of dynamical M / L in the context of UCDs.

Several effects can cause an overestimate in dynamical mass, and thus an overestimate of M / L. For example, the orbital motions of binary stars can inflate a system's observed velocity dispersion. A recent, multi-epoch velocity study of Segue 1 suggests that binaries should not pose a major problem for the dynamical classification of systems with intrinsic velocity dispersions of at least a few km s^-1 (Martinez et al. 2011, Simon et al. 2011). However, binaries do materially impact lower velocity dispersion systems (Bradford et al. 2011), and models based on more extreme assumptions than previously considered identify regions of parameter space where binaries could impact Segue 1-like velocity dispersion systems (McConnachie & Côté 2010). Tidally unbound and MW foreground stars can also contaminate spectroscopic samples of a MW companion's stars and inflate its observed velocity dispersion. The effect of such contaminants can be mitigated by a combination of careful simulations of the MW foreground and its color-magnitude-velocity distribution (Willman et al. 2011), the use of spectroscopic abundance indicators, statistical approaches to identifying object members (e.g., Walker et al. 2009b), and approaches to eliminating tidally stripped stars that have been informed by N-body simulations (Klimentowski et al. 2007).

Other effects may alternatively cause an underestimate of stellar mass, and thus an overestimate of the presence of non-stellar mass. For example, Hernandez (2012) shows that the lowest luminosity systems (L ~ 500 L) can have (M / L)_stellar between 1 and 10 simply from the stochastic effects of sampling an IMF with a small number of stars. A tidally stripped, dynamically relaxed (and therefore mass-segregated) GC can also have a super-stellar M / L once the majority of its mass has been lost. Models of star cluster evolution that include the effects of mass segregation and the Galaxy's tidal field have shown that high fractions of stellar remnants accumulate in the center as a cluster is stripped of mass (Vesperini & Heggie 1997, Giersz 2001, Baumgardt & Makino 2003). Although possible, it should be rare to observe a system so tidally stripped that its global M / L is significantly inflated by this mechanism. For example, although Palomar 5 is estimated to be ~ 100 Myr from complete destruction (less than 1% of its total lifetime), it is observed to have M / L_dyn < 1 (Odenkirchen et al. 2002, Dehnen et al. 2004). Observational limitations may also generate ambiguity in the dynamical classification of the lowest luminosity (L < 1000 L) and low velocity dispersion (< 3 km s^-1) systems. For example, Segue 3 (L = 90_-40⁺⁹⁰ L, d ~ 17 kpc) contains only a few dozen member stars brighter than r = 22. 32 of Segue 3's stars were observed with Keck/DEIMOS to obtain velocity measurements with uncertainties per exposure per star of ~ 3-10 km s^-1 (Fadely et al. 2011). With a _los of 0.3 km s^-1 expected based on stars and Newtownian gravity alone, its measured velocity dispersion of 1.2 ± 2.6 km s^-1 is dynamically consistent with either a galaxy or a star cluster interpretation. Even with techniques which retrieve stellar velocities from medium-resolution spectra with uncertainties < 1 km s^-1 (Koposov et al. 2011), star-poor systems need to reside within ~ 20 kpc for there to be a sufficient number of stars bright enough to spectroscopically observe with high S/N with a 10m-class telescope.

3.2. [Fe/H] Spread

Another way to directly constrain the potential well in which a system formed is the presence of an [Fe/H] spread. The use of [Fe/H] as a diagnostic for our proposed galaxy definition is supported by a combination of models of supernova winds in low-mass systems and the observed abundances of stars in well-studied dwarfs and GCs. Iron is produced by supernovae (both Type II and Ia), so a dispersion in [Fe/H] implies that the system was able to retain supernova ejecta to form multiple generations of stars. The energetic winds of supernovae can only be retained in a gravitational well of sufficient depth. Estimates for the GC mass needed to retain SN ejecta are > few × 10⁶ M (e.g., Dopita & Smith 1986, Baumgardt et al. 2008). Observed [Fe/H] spreads of over 1 dex combined with inferred stellar masses of ~ 1000 M or less have thus contributed to a galaxy classification for both Segue 1 and Willman 1 (Martin et al. 2007, Norris et al. 2010, Simon et al. 2011, Willman et al. 2011).

3.2.1. Calculating _{[Fe / H]}

To empirically investigate the difference in [Fe/H] spread, _{[Fe / H]}, between well-studied dwarf galaxies and GCs, we estimate the spread and associated uncertainty for each of 16 dwarfs and 24 GCs with publicly available, spectroscopic [Fe/H] measurements. We only used [Fe/H] measurements based on actual iron lines, rather than studies that infer iron abundance from the calcium triplet or photometry. We used Bayesian Markov Chain Monte Carlo techniques to fit a normal distribution to the stellar [Fe/H] values for each object, taking into account the reported measurement uncertainties and assuming flat priors. ⁵ We summarize the standard deviation of each sample, _{[Fe / H]}, as the median of its posterior distribution, together with a 68.2% credible interval (analogous to the usual 1 confidence interval). Calculated values of [Fe/H], _{[Fe / H]}, associated uncertainties, and references are summarized in Table 1. The uncertainties on the variances are an increasing function of decreasing sample size, because small samples poorly sample the underlying [Fe/H] distribution.

Table 1. [Fe/H] properties of MW globular clusters and dwarfs

Name	[Fe / H]	±34% CL	[Fe / H]	+34% CL	-34% CL	MV	Nstar	Ref	type
Cen	-1.647	0.009	0.271a	0.007	0.007	-10.3	855	J10	GC
M54	-1.559	0.021	0.186	0.016	0.014	-10.0	76	Car10	GC
NGC 6441	-0.334	0.018	0.079	0.016	0.013	-9.6	25	G07	GC
NGC 104	-0.743	0.003	0.024	0.003	0.002	-9.4	147	Car09b	GC
NGC 2419	-2.095	0.019	0.032	0.013	0.009	-9.4	38	Coh10	GC
NGC 2808	-1.105	0.006	0.062	0.005	0.004	-9.4	123	Car06	GC
NGC 6388	-0.404	0.014	0.071	0.012	0.010	-9.4	36	Car09b	GC
NGC 7078	-2.341	0.007	0.055	0.006	0.005	-9.2	84	Car09b	GC
NGC 5904	-1.346	0.002	0.014	0.002	0.002	-8.8	136	Car09b	GC
M22	-1.764	0.016	0.099b	0.013	0.011	-8.5	37	M11	GC
NGC 1851	-1.157	0.005	0.046	0.004	0.003	-8.3	124	Car11	GC
NGC 1904	-1.545	0.005	0.028	0.005	0.004	-7.9	58	Car09b	GC
NGC 6752	-1.564	0.004	0.034	0.003	0.003	-7.7	137	Car07b	GC
NGC 6809	-1.970	0.004	0.035	0.003	0.003	-7.6	156	Car09b	GC
NGC 3201	-1.495	0.004	0.042	0.004	0.003	-7.5	149	Car09b	GC
NGC 6254	-1.557	0.005	0.048	0.004	0.003	-7.5	147	Car09b	GC
NGC 7099	-2.358	0.006	0.037	0.006	0.005	-7.5	65	Car09b	GC
NGC 4590	-2.230	0.007	0.057	0.006	0.005	-7.4	122	Car09b	GC
NGC 6218	-1.313	0.004	0.027	0.004	0.003	-7.3	79	Car07a	GC
NGC 6121	-1.200	0.003	0.018	0.003	0.002	-7.2	103	Car09b	GC
NGC 6171	-1.066	0.008	0.037	0.007	0.006	-7.1	33	Car09b	GC
NGC 288	-1.219	0.004	0.034	0.004	0.003	-6.8	110	Car09b	GC
NGC 6397	-1.994	0.004	0.027	0.003	0.003	-6.6	144	Car09b	GC
NGC 6838	-0.806	0.006	0.027	0.005	0.005	-5.6	39	Car09b	GC
For	-1.025	0.012	0.292	0.010	0.010	-13.3	675	K10	dwarf
Leo I	-1.450	0.011	0.276	0.009	0.008	-11.9	827	K10	dwarf
Scl	-1.726	0.024	0.452	0.019	0.017	-11.2	376	K10	dwarf
Leo II	-1.670	0.024	0.347	0.020	0.018	-10.0	258	K10	dwarf
Sex	-1.966	0.039	0.339	0.033	0.030	-9.6	141	K10	dwarf
Dra	-1.946	0.024	0.354	0.020	0.019	-8.8	298	K10	dwarf
CVn I	-1.962	0.038	0.441	0.032	0.029	-8.6	174	K10	dwarf
UMi	-2.112	0.027	0.319	0.025	0.023	-9.2	212	K10	dwarf
Herc	-2.518	0.140	0.583	0.124	0.095	-6.2	21	K08	dwarf
UMa I	-2.334	0.128	0.638	0.106	0.086	-5.5	31	K08	dwarf
Leo IV	-2.363	0.230	0.695	0.210	0.149	-5.5	12	K08	dwarf
Cvn II	-2.444	0.178	0.621	0.164	0.120	-4.6	15	K08	dwarf
UMa II	-2.357	0.204	0.563	0.204	0.136	-4.0	9	K08	dwarf
ComBer	-2.640	0.100	0.382	0.088	0.070	-3.8	23	K08	dwarf
Wil1	-2.110	0.367	0.557	0.577	0.231	-2.7	3	W11	dwarf
Seg 1	-2.735	0.389c	0.752	0.417	0.227	-1.5	7	N10, S11	dwarf
The reference column gives the source of individual [Fe/H] measurements used to estimate the dispersion in each object. For Segue 1, only the one star (Seg 1-7) is taken from Norris et al. (2010). Values of MV for the dwarfs are from Sand et al. (2011) and references therein. Values of MV for the GCs are from Harris (Harris 1996, 2010 edition). The posterior distribution of [Fe / H] sufficiently symmetric that we only quote a single value for ± 34% CL, taking the average of the + and - values in the small number of cases with a few thousandth of a dex difference between the two.. Reference key: J10 = Johnson & Pilachowski (2010), Car11 = Carretta et al. (2011), Car10 = Carretta et al. (2010a), Coh10 = Cohen et al. (2010), Car09b = Carretta et al. (2009b), Car06 = Carretta et al. (2006), M11 = Marino et al. (2011), Car07a = Carretta et al. (2007a), G07 = Gratton et al. (2007), Car07b = Carretta et al. (2007b), K10 = Kirby et al. (2010), K08 = Kirby et al. (2008), W11 = Willman et al. (2011), N10 = Norris et al. (2010), S11 = Simon et al. (2011)
a This value is a lower limit (see Section 3.2.1).
b This value is an upper limit (see Section 3.2.1).
c Unlike the other objects, the metallicity of Segue 1 has asymmetric uncertainties: -2.735-0.405+0.373

A few notes on unusual cases: For Segue 1, we included the star from Simon et al. (2011) with only an upper limit to its [Fe/H] as a censored datum in our analysis. We used the largest set of [Fe/H] values for Centauri (Johnson & Pilachowski 2010). However, this sample is biased against the most metal-rich subpopulation because it is magnitude-limited in V. We thus consider our estimate of its [Fe/H] spread to be a lower limit. The Marino et al. (2011) data for M22 does not contain uncertainties, and so our reported _{[Fe / H]} is an upper limit. Our analysis does not include the Terzan 5 GC despite claims of an [Fe/H] spread in this object (Ferraro et al. 2009, Origlia et al. 2011), owing to its ~ solar abundance (and thus different origin than the old metal-poor stellar populations we are primarily considering) and the possibility that the sample may be partially contaminated by bulge stars. We also did not include NGC 5824, in which Saviane et al. (2012) have reported _{[Fe / H]} ~ 0.11 - 0.14 dex, because this measurement is based on the Calcium triplet (thus revealing a Ca spread, not necessarily an Fe spread). The GC NGC 2419 is known to display a ~0.2 dex spread in Ca, but none in Fe (Cohen et al. 2010).

Although reasonable indicators of the dispersion in [Fe/H], the values in Table 1 should be considered with caution before comparing in detail with models. The accuracy of our estimates of the variance of [Fe/H] (and its uncertainty) rely on (i) the appropriateness of the underlying Gaussian model, (ii) clean membership samples, and (iii) accurate uncertainties for individual stars. For the fainter dwarfs in this set the first condition rarely holds (e.g., Kirby et al. 2011), so our estimated variances should be taken as indicators of the spread in metallicity rather than as exact values. The faintest dwarfs may also have a small number of interloper stars in their membership samples (see also Section 3.2.4). The third condition - estimating accurate uncertainties - is most relevant for GCs, because their measured _{[Fe / H]} are comparable to (or less than) the measurement uncertainties for single stars. For this paper, we have included the random uncertainty in the Fe1 abundance as the standard error of the mean, while Carretta et al. (2009a) included no measurement uncertainties in their calculation of [Fe/H] spread. The practical effect is that the intrinsic [Fe/H] spreads we derive for GCs in this paper are slightly smaller than those in Carretta et al. (2009a), by typically 0.01 dex. Like Carretta et al. (2009a), we emphasize that their and our values are upper limits to be true [Fe/H] spreads because of our limited ability to model the full measurement uncertainties on each star (see Carretta et al. 2009a for detailed discussion of the relevant modeling issues).

3.2.2. _{[Fe / H]} in M_V -10 Objects

Figure 1 shows _{[Fe / H]} for MW dwarf galaxies (filled, black circles) and MW GCs (open red circles) as a function of absolute magnitude. Uncertainty bars show the 68.2% confidence intervals. We show objects with dynamical classifications of galaxy or star cluster as different symbols in Figure 1 to highlight the regime in which _{[Fe / H]} results in the same inference about a system's potential well as a dynamical study. This tests whether _{[Fe / H]} may be used as a galaxy diagnostic in cases where dynamical studies are inconclusive.

This figure shows a striking difference between the [Fe/H] spreads observed for dwarf galaxies and GCs. The dwarfs all have spreads of 0.3-0.7 dex (even higher for Segue 1), whereas none of the GCs less luminous than M_V = -10 have substantial [Fe/H] dispersions. After the upper limit of _{[Fe / H]} = 0.1 dex estimated for M22, the next highest spread is 0.08 dex estimated for NGC 6441. Although these values are small, they are formally greater than zero with > 99% probability (as calculated above). These estimates may reflect the detection of minor star-to-star variations in [Fe/H] in GCs less luminous than M_V = -10. However, in light of the caveats given above, they may yet be found to be consistent with no star-to-star variation in [Fe/H].

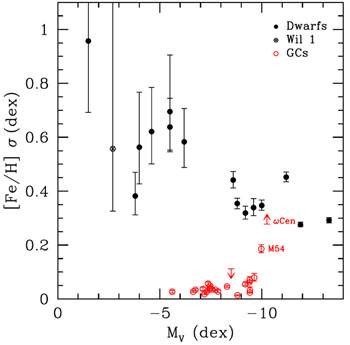Figure 1. The dispersion in [Fe/H] measured for MW dwarf galaxies (black, filled) and globular clusters (red, open), calculated assuming an underlying Gaussian distribution. The systems shown with dwarf galaxy symbols in this figure have been independently classified as galaxies by dynamical studies. Willman 1 does not have a definitive dynamical classification, and so is shown as an open hexagon with a cross. By this figure, a galaxy classification can be indirectly inferred from Willman 1's spread in [Fe/H]. The presence of a spread in [Fe/H] can diagnose a galaxy definition because it constrains the depth of the potential well in which a system formed, as supernova ejecta must be retained to form further generations of stars. Error bars show the estimated uncertainty on each dispersion given the [Fe/H] measurement uncertainties on the individual member stars. Values and references are summarized in Table 1. Figure 7 of Carretta et al. (2010a) shows a figure similar in spirit to this, but for a smaller set of objects and without measurement uncertainties.

3.2.3. _{[Fe / H]} in M_V -10 Objects

The interpretation of the _{[Fe / H]} spreads observed in the two GCs more luminous than M_V = -10, M54 and Cen, is less straightforward. One interpretation of the spreads in M54 and Cen is that they are the nuclear star cluster cores remaining from a stripped dwarf galaxy (M54: Sgr core, Sarajedini & Layden 1995; Cen, Lee et al. 1999, Bekki & Freeman 2003). It remains to be seen whether the properties of the gravitationally bound remains of such a stripped galaxy would satisfy our definition of a galaxy, and be formally classified as such. Recent observations have discovered a significant amount of tidal debris that may be associated with Cen (Majewski et al. 2012). Sgr is already a classified galaxy, so M54 would not be considered a separate entity.

An alternative interpretation of the [Fe/H] spreads in these M_star > 10⁶ M clusters is self-enrichment by SNe without the additional gravitational influence of dark matter or a non-Newtonian effect. This interpretation is complicated by the fact that M54 and Cen do not actually have the highest escape velocities of the GCs in our sample. Using the fitted relation between central velocity dispersion and central escape velocity, v_esc,0 / ₀ = 3.7 + 0.9(c-1.4), from Gnedin et al. (2002), we find that 8 of the 62 GCs with velocity dispersions reported in the 2010 edition of Harris (1996) have central escape velocities larger than M54's v_esc,0 ~ 45 km s^-1(not including Cen). 5 of these (47 Tuc, NGC 2808, NGC 6388, NGC 6441, and M15) are in our sample and do not display [Fe/H] spreads 0.1 dex. NGC 6441 and 6388 have escape velocities of 72 and 76 km s^-1, respectively, larger than Cen's escape velocity of 61 km s^-1. A caveat to this analysis is that these values are measured at the present day. At earlier times, these GCs were all more massive but have since undergone stellar evaporation and tidal mass loss; some may have also had different sizes. All of these factors could have affected their relative abilities to retain supernova ejecta.

Observations of GCs in other galaxies provide tentative support for self-enrichment in iron in M_V < -10 GCs. For example, HST/ACS photometry of three of the most massive GCs in M31 are suggestive of spreads in [Fe/H] on the red giant branch (Fuentes-Carrera et al. (2008)). The dynamical masses of these GCs range from 2-6 × 10⁶ M, comparable to or larger than Cen (Strader et al. 2011). The M31 cluster G1 (3 × 10⁶ M) also may have a significant [Fe/H] spread (Meylan et al. (2001)).

Separately, a number of groups have identified evidence of self-enrichment in extragalactic GCs. Precise photometry of blue, metal-poor GCs in a variety of galaxies (Harris et al. 2006, Mieske et al. 2006, Strader et al. 2006, Spitler et al. 2006, Forbes et al. 2010, Mieske et al. 2010) shows a correlation between magnitude and color for metal-poor GCs. This mass-metallicity relationship is not observed in all galaxies studied, but a typical relation is Z ~ M^0.4, where Z is the mean metallicity of the GC and M is its mass. The onset of the correlation appears to be between ~ 2 × 10⁵ and 10⁶ M. The slope and onset mass of the correlation can be reasonably explained by models in which the GCs self-enrich in iron (Bailin & Harris 2009, Strader & Smith 2008).

If (nearly) all GCs with stellar masses above few × 10⁶ M display [Fe/H] spreads, then it is likely these spreads accrue from self-enrichment without the help of an additional gravitational field. More extensive spectroscopic and photometric campaigns to quantify the [Fe/H] spreads of extragalactic GCs will be essential to develop a fuller picture of the connection between _{[Fe / H]} and the formation channel(s) of objects with M_V < -10.

3.2.4. A Relationship Between _{[Fe / H]} and M_V For Dwarfs?

Figure 1 displays another striking trend in addition to the dwarf/GC dichotomy: the apparent increase in _{[Fe / H]} with decreasing luminosity (see also Section 6.2 of Kirby et al. 2011). While the dispersion in [Fe/H] for most MW dwarf galaxies with M_V < -8 (the classical dwarfs) is 0.3-0.4 dex, the dispersion for most of the lower luminosity dwarfs (the ultra-faint dwarfs) is 0.5-0.6 dex. The most likely explanations for this apparent trend are: (i) a true physical difference in the _{[Fe / H]} of the least luminous systems, (ii) a systematic bias in the calculated _{[Fe / H]} as the model assumptions become increasingly poor with decreasing luminosity, or (iii) a result of a low level of foreground contamination that disproportionately affects spectroscopic samples of the lowest surface brightness systems. The faintest dwarfs have tails at the metal-richer ends of their metallicity distribution functions that are not present in the classical dwarfs. It is not yet clear whether those metal-richer tails are physical or a result of mild contamination in the samples. Exploring the relative likelihood of these three scenarios is beyond the scope of this paper, but will be imperative to pursue in the future.

3.3. Indirect Diagnostics: Population Arguments

Population arguments rely on the assumption of a single classification for all astrophysical objects known to populate a particular region of parameter space. Such arguments are handy because, for example, it would be both impractical and unnecessary to conduct a detailed analysis of each of the 200 million galaxies cataloged by the eighth Sloan Digital Sky Survey data release (Aihara 2011) before classifying them as such. The most common population-based classification is simply the size-based classification that is naturally made for galaxies with scale size 1 kpc. All objects satisfying this "I know it when I see it" criterion that have been studied in sufficient detail have been kinematically shown to satisfy our proposed definition of galaxy (not including tidal dwarfs, see Section 4.4.) Some kinematic studies of galaxies have postulated that no unseen matter or modification of Newtonian gravity may be needed to explain their dynamics (e.g., Romanowsky et al. 2003). However, such studies have always been shown to be flawed on theoretical grounds (e.g., Dekel et al. 2005) or were refuted by subsequent observational studies.

Attempts have been made to connect, or distinguish, galaxies and star clusters using scaling relations that combine their metallicities, effective sizes, internal velocities, luminosities or derivatives thereof. Such studies have recently focused on variants of the Fundamental Plane such as the Fundamental Manifold (Forbes et al. 2011, Zaritsky et al. 2011) and the Fundamental Curve (Tollerud et al. 2011). These scalings reveal similarities and differences in the ways baryons coalesce within different types of systems. However, the scalings do not seem to shed light on the classification of objects as a star cluster or a dwarf galaxy, in a way more meaningful than M / L within r_half (e.g., Forbes et al. 2008, Tollerud et al. 2011, Zaritsky et al. 2011). One simple difference between galaxies and globular clusters as a population is the metallicity-luminosity relation observed for galaxies (but not star clusters, UCDs, or nearby tidal dwarfs) over a wide range of stellar masses (e.g. Skillman et al. 1989, Tremonti et al. 2004, Woo et al. 2008, Kirby et al. 2011). Although the metallicity and luminosity of an individual object would not be sufficient to classify it as a galaxy or star cluster, consideration of the metallicities and luminosities of a population of objects may aid in its classification (see also Section 4.2.2). It is also worthwhile to consider the placement of individual ambiguous objects with respect to observed scaling relations. Inconsistency with well-established relationships on a case-by-case basis may be a sign that some of the cautions raised in Section 3.1.1 are affecting the kinematics, effective mass, or size measured for an object.

Another approach to population-based classification is to include a broad set of properties such as spatial distribution, metallicity, and orbits when looking for subtle trends within a diverse set of observables. The combination of such a set of clues may help reveal whether some object or type of object with an ambiguous classification has an origin (and thus, possibly, classification) more similar to that of star clusters or of dwarf galaxies. Brodie et al. 2011 recently conducted a thorough analysis of UCDs around M87 in the Virgo cluster. They combined size-luminosity, age-metallicity, spatial distribution, and orbital dynamics to infer the possible co-existence in size and luminosity of three sub-populations of UCDs: the stripped nuclei of dEs, remnants from more massive red galaxies (either their nuclei or merged clusters), and genuine star clusters.

Although we do not aim to be exhaustive, throughout Section 4 we will mention some specific indirect diagnostics that may contribute to a galaxy classification.

⁵ The relevant (simple) code is available on request. Back.