

Spirals galaxies represent some of the most beautiful, and fascinating objects in the Universe. According to the Galaxy Zoo project, spiral galaxies make up about two thirds of all massive galaxies, whilst around one third are ellipticals, and a few per cent merging galaxies (Lintott et al., 2011, Willett et al., 2013). Star formation overwhelmingly occurs in spiral galaxies, and in particular is associated with spiral arms. Thus understanding the nature of spiral arms is essential both for understanding star formation, and galaxy evolution.
Spiral galaxies are generally classified into different types according to the presence of a bar (S and SB for unbarred and barred galaxies, and sometimes SAB for weakly barred galaxies) and the degree of winding (or pitch angle) of the spiral arms (Hubble, 1926b, Reynolds, 1927, de Vaucouleurs, 1959). The latter is scaled from Sa-Sd or SBa to SBd with the 'd' classification representing the most open arms, and the 'a' classification the most tightly wound. The sequence also represents a decrease in the size and luminosity of the bulge from Sa (or SBa) galaxies to Sd (or SBd), and an increase in gas content from Sa to Sd galaxies.
A second classification scheme was proposed by Elmegreen & Elmegreen (1982) and Elmegreen & Elmegreen (1987) to classify spiral galaxies into 12 types according to the number and length of spiral arms. Thus galaxies with many fragmented short arms are different types to those with two long arms. Galaxies could also be denoted as having two inner arms, and multiple outer arms. A simpler, but similar division of spiral galaxies (see e.g. Elmegreen 1990) is into 3 types: flocculent spiral galaxies (with many short arms, such as NGC 2841), multi-armed spirals (e.g. M33) and grand design galaxies (with two main spiral arms, e.g. M51). All of these types may or may not exhibit bars. Around 60%, of galaxies exhibit some grand design structure, either in the inner or entire part of the disc (Elmegreen & Elmegreen, 1982, Grosbøl et al., 2004).
The Hubble classifications are usually associated with the long-term evolution of galaxies, whereas the classification by Elmegreen is instead associated with their current properties and environment. Historically, Sa galaxies, and ellipticals were termed early type galaxies, whilst Sc and Sd galaxies were termed late type galaxies, though this is opposite to the evolutionary sequence which has since been established. Instead trends in star formation rate, bulge-to-disc ratio, and age of disc stars now indicate an evolutionary sequence from Sc to Sa types (Sandage, 1986, Kennicutt, 1998). Sa type galaxies are thought to have already used up much of their gas and exhibit lower star formation rates compared to Sc and Sd types, although mergers and galaxy interactions will also influence the properties of the galaxies (e.g. Elmegreen 1990). We also note correlations with Hubble type are only a general trend - Kennicutt (1981) indicates that the pitch angle correlates only in an average sense with galaxy type, and there is quite substantial spread.
The flocculent, or grand design nature of spiral galaxies, is directly linked to the mechanism which generates the spiral arms. There are three main mechanisms hypothesised to produce spiral arms, i) (quasi-stationary) density wave theory, ii) local instabilities, perturbations, or noise which are swing amplified into spiral arms, and iii) tidal interactions. Bars may also play a role in inducing spiral arms. Note that these mechanisms are not necessarily mutually exclusive, for example a tidal interaction could theoretically induce a wave which obeys density wave theory. Typically though, local instabilities are associated with flocculent or multi-armed galaxies, whereas grand design galaxies are presumed to have undergone a tidal interaction, have a bar driving arms, and/or obey steady state density wave theory. In addition to the various classifications of spiral galaxies, and spiral arm formation mechanisms, there are also three kinematic types of spiral arm i) material arms, which obey the kinematics of the disc, ii) kinematic spiral arms, which rotate slower than the angular velocity of the disc, and iii) stationary spiral arms, which rotate rigidly and do not wind up. In the following sections we discuss these (and a few other) supposed mechanisms, and which type of spiral arms, and spiral galaxies are produced.
There are also several simple properties of spiral arms that we can observe that can give insight on the nature of spiral arms (we go into much more depth on observational tests for spiral arms in Section 4), i) the number of spiral arms, ii) the pitch angle, iii) amplitude, iv) arm shape and v) lifetime. How many spiral arms a galaxy exhibits is one of the most fundamental questions regarding the theory of spiral arms. In the absence of a bar, or perturber, this will most simply depend on the relative disc and halo masses, and their dimensions. A galaxy will only form spiral arms at all if the disc is sufficiently gravitationally dominated. To a rough approximation (the susceptibility of the disc to asymmetric perturbations) this is governed by the Toomre parameter Q for stars and/or gas (see Section 2.1.1). If the disc is unstable, an estimate of the expected number of spiral arms can be made by considering the stability of different wavenumbers in the appropriate dispersion relation (i.e. the value of k, the wavenumber, such that e-iω(k) t grows fastest). Alternatively, and more appropriately for perturbations growing from local instabilities or noise, the number of arms can be estimated by swing amplification theory, as described in Section 2.2.1, where again the number of spiral arms corresponds to the value which produces the greatest amplification. Tidally interacting galaxies naturally produce two-armed spiral galaxies.
Other observable properties of spiral arms were investigated by Kennicutt 1981, and many other works since (e.g. Considere & Athanassoula (1988), Block et al. (1994), Puerari & Dottori (1992), Seigar & James (1998), Ma (2002), Seigar et al. (2006), Elmegreen et al. (2011), Kendall et al. (2011)). Although the pitch angle is historically used to classify galaxies according to the Hubble sequence, the differences in spiral arm shape, i.e. the pitch angle of the spiral arms appears to be most dependent on the maximum rotation velocity, and thus the local shear in the disc, rather than the global mass distribution (Kennicutt, 1981, Kennicutt & Hodge, 1982, Garcia Gomez & Athanassoula, 1993, Seigar & James, 1998, Seigar et al., 2006). For example Figures 8 and 10 of Kennicutt (1981) show that the pitch angle correlates much better with the maximum rotational velocity than the properties of the bulge. However there is still considerable scatter (see Figure 7 of Kennicutt (1981)) in the correlation with rotation velocity that there is scope for tidal interactions, or density wave theory to introduce some spread (see also Grand et al. (2013)). There is also no correlation with pitch angle and arm class, i.e. the Elmegreen classification scheme of whether the galaxy is flocculent or grand design (Puerari & Dottori, 1992). Kennicutt (1981) also examined the shapes of spiral arms, finding that they did not fit exactly into the category of either density wave theory (logarithmic) or tidally induced (hyperbolic spirals). The lifetimes of spiral arms are obviously much more difficult to test observationally (see Sellwood (2011)). Here we have relied more on computer simulations, and theory to predict the lifetimes of spiral arms for different scenarios. Generally though, arms in flocculent galaxies are expected to be fairly short lived (few 100 Myrs) and arms in grand design spirals somewhat longer lived (∼ 1 Gyr).
Although so far we have discussed spiral galaxies as either flocculent or grand design, observations in the 1990s showed that galaxies could exhibit characteristics of both flocculent and grand design structure, typically with grand design arms seen in the infrared (old stars) and a more flocculent structure seen in the optical (gas and young stars) (Block & Wainscoat, 1991, Thornley, 1996, Thornley & Mundy, 1997). Some galaxies also appear to exhibit a 3 armed structure in the optical and 2 armed in the IR (Block et al., 1994). The existence of such galaxies poses a further challenge for theories of spiral structure.
The main previous review on spiral structure is Toomre (1977), though there have also been a couple of shorter reviews by Sellwood in recent years (Sellwood, 2010b, Sellwood, 2011). A historical review of spiral arm theory in the 1960s and 70s is also given by Pasha (2004a), Pasha (2004b). A review specific to the Milky Way is currently being written by Benjamin (Benjamin 2014, in preparation). In this review, we aim to bring together the different aspects of studies of spiral structure including simulations and observational tests, as well as the theory. The outline of this review is as follows. In Section 1.1, we discuss the historical context of spiral galaxies, and the origin of different theories for spiral structure. In Section 2 we go into much more detail on the possible mechanisms for generating spiral structure, including density wave theory, swing amplification, bars, tidal interactions, stochastic star formation and dark matter halos. We also include discussion of computer simulations to test these theories. In Section 3 we examine the gas response to spiral arms, including again density wave theory, local instabilities and tidal perturbations. In Section 4 we discuss possible observational tests to distinguish between the various scenarios of spiral structure. Finally in Section 5, we present our conclusions.
For a comprehensive review of the history of spiral structure, we recommend Pasha (2004a), Pasha (2004b), who gives a very detailed, and personal description of the developments in spiral structure, particularly in the 1960s. Here we given a brief overview up to about the time of the Toomre (1977) review, although much of the background theory is also considered in much more detail in Section 2.
Spiral galaxies have been observed for over 150 years, although until the 1920s, they were classed as 'spiral nebulae', and assumed to lie within our own Galaxy. The spiral structure of M51 was identified by Lord Rosse in 1850 (Rosse, 1850) as the first spiral nebulae (Figure 1). Rosse also identified point sources within these nebulae, hence establishing that they were not simply clouds of gas. The Curtis-Shapley 'Great Debate' then later ensued about whether these nebulae were extragalactic. This matter was clarified by Hubble, who confirmed that the spiral nebulae were indeed external to the Milky Way, and thus spiral galaxies, by determining the distance first to M33, and then M31, using Cepheid variables (Hubble, 1926a, Hubble, 1929). The distances to M31 and M33 demonstrated that these objects were far too distant to lie within the Milky Way.
 |
Figure 1. A sketch of M51 by Lord Rosse (Rosse, 1850). |
Following the establishment of the nature of spiral nebulae, astronomers considered the nature of the spiral arms themselves. The first main proponent of this work was Lindblad, who first considered spiral arms in terms of Maclaurin ellipsoids (flattened spheroids rotating in an equilibrium state) (Lindblad, 1927), following previous work by Jeans and Poincare. He considered an instability occurring at the edge of an ellipsoid, which induces high eccentricity in the orbits at the outer edges, pertaining to circular orbits nearer the centre. Lindblad (1935) later derived a condition for gravitational instability, and thereby spiral arms, in a series of rotating spheroids. Lindblad wrote that spiral arms are analogous to a harmonic wave in an unstable Maclaurin spheroid (Lindblad, 1927, Lindblad, 1940). He considered spiral arms in terms of individual stellar orbits (and indeed, Kalnajs (1973) later showed that a spiral perturbation can be represented by a series of unaligned elliptical orbits) rather than a collective process. The idea of spiral arms as a wave was not actively considered until the 1960s.
The 1960s in fact saw the next major development in spiral arm theory, when indeed spiral arms started to be considered as collective processes governed by the gravity of the galactic disc. The pioneering work of Toomre (1964) and Lin & Shu (1964) (following also the stability analysis of Safronov (1960) for discs) studied gravitational instabilities in the context of an infinitesimally thin, rotating, stellar disc. Both papers started with the linearised equations of motion, and Poisson's equation for a stellar disc, and established solutions which have the Fourier decomposition (Shu, 1992, Binney & Tremaine, 2008):
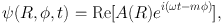 |
(1) |
where Ωp = ω / m and Ωp is the angular velocity of the perturbation, or pattern speed. Equation 1 assumes that the complex function A(R), which determines the amplitude and radial phase of the perturbations, varies slowly with R (the tight winding approximation, see Section 2.1.1). Thus these solutions represent waves with crests at periodic displacements. In addition to the form of the wave, these results also established the dispersion relations for fluid and stellar discs (with Lin & Shu (1966), and Kalnajs (1965)), and the stability criteria for discs subject to axisymmetric perturbations (see Section 2). At this point however, there is complete flexibility regarding the value of m (the number of arms), the superposition of waves of different m, what range of R or φ the solution covers, the sign of Ωp, and thus whether the arms are leading or trailing, or the length of time the perturbation exists.
Lin & Shu (1964) proposed that in fact there is a preference for lower values of m, and that such waves are relatively stable with time. Lin & Shu (1964), Lin & Shu (1966) also proposed a global solution for the disc, rather than the local perturbations assumed by Toomre (1964). Such global stable waves would be standing waves in the disc, and hence they were called 'quasi-stationary', a term first introduced by Lindblad (1963). The motivation for supposing the stability of these waves, in particular for m = 2 was largely observational. Most galaxies were observed to be spirals at that time (Hubble, 1943), so either the spiral arms are long lived, or they are continually replenished. Furthermore, fixed spiral arms would remove the so called 'winding problem'. In addition, disproportionately many galaxies have 2 spiral arms, so a tendency for systems to exhibit m = 2 would explain this predominance.
Goldreich & Lynden-Bell (1965a), consider the action of gravitational instabilities, first in a uniformly rotating gas disc, then under differential rotation (Goldreich & Lynden-Bell, 1965b). They supposed that spiral arms are a superposition of many unstable wavelengths in the gas. In their picture, it is the instabilities in the gas which form gaseous spiral arms, which in turn form stars and lead to stellar spiral arms. This is somewhat different from the picture of a stellar dominated disc, where instabilities are thought to arise in the stars, leading to a gravitational potential well for the gas to fall into, shock and form molecular clouds (see Section 3.7). Unlike the simpler analysis of discs subject to axisymmetric perturbations (see Section 2), these studies investigate asymmetric perturbations in a shearing disc. Goldreich & Lynden-Bell (1965b), and Julian & Toomre (1966), demonstrated the significance of a differentially rotating disc. Gravity is enhanced as a region undergoes shear. Hence it is easier for perturbations to grow via the disc self gravity. This effect was later coined swing amplification, discussed further in Sections 2.1.3 and 2.2.
Meanwhile there were some important observational developments following the theoretical work of Lindblad. One was the finding that spiral arms tended to be trailing in character (Hubble, 1943). A second was that, rather than uniform rotation, galaxies were indeed observed to rotate differentially (e.g. Burbidge & Burbidge (1964), Rubin & Ford (1970)).
In the late 60s, and 70s, authors started to consider the response of gas to the stellar disc. Assuming a static spiral potential of the form proposed by Lin & Shu (1964), the solution for the gas response can be obtained (Fujimoto, 1968, Roberts, 1969). In particular the gas is found to undergo a shock caused by the stellar spiral spiral arms. The detection of dark dust lanes alongside spiral arms (Sandage, 1961, Lynds, 1970) gave strong observational evidence that the gas undergoes a spiral shock, the dense shock being seen as dark clouds in the dust lanes that go on to form stars (Roberts 1969). In fact it is now evident that regardless of how spiral arms are generated, spiral structure is only very weak in the old stars, whereas the spiral structure we see by eye is dominated by the gas and young stars (e.g. Elmegreen et al. (2011)).
At the same time however, results were starting to query whether steady spiral modes could be sustained in galaxies. Lynden-Bell & Ostriker (1967) showed, in the 'anti-spiral theorem' that stable spiral modes do not exist in a steady state, although it is possible to obtain a solution with asymmetric spirals, i.e. one trailing and one Toomre (1969) also showed that the waves will not remain in a fixed position within the disc, rather the pattern will propagate inwards to outwards with the group velocity on a timescale of a few galactic rotations - suggesting that density waves need to be constantly replenished. Consequently, a mechanism to maintain density waves was required. Mark (1974), Mark (1976) suggested that it could be possible to maintain spiral density waves by means of reflection between two radii of the disc - setting up a standing wave. Toomre (1969) instead proposed tidally interacting galaxies were the primary means of generating m = 2 spiral structure.
Since the 1970s, the debate about stationary versus transient spirals has continued. In addition to theoretical arguments, numerical simulations have become much more widespread to test theories of spiral structure. Observations are also starting to provide some information on the dynamics of spiral galaxies.