1. INTRODUCTION

Galaxies show a wide variation in morphological appearance, due to the complex processes of galaxy formation and evolution. Both initial conditions and interactions between galaxies can play an important role. For instance, most elliptical galaxies are believed to be the result of major mergers of galaxies (Toomre & Toomre, 1972, Schweizer, 1986, Barnes & Hernquist, 1992). Consequently the morphology of galaxies is connected to the local environment, as is evidenced by the well-established morphology-density relation (e.g. Dressler, 1980). The connection between morphology and galaxy formation and evolution was made early-on, most notably by Hubble [1926] who believed that elliptical galaxies would eventually transform into grand-design spiral galaxies. Although this picture has been reversed in recent years, the importance of morphology has remained. Of the various observables that can be used to describe the appearance of a galaxy, its shape is one of the most important.

As it was realised that galaxies may influence each other, other questions become relevant for our understanding of galaxy formation and evolution, such as “Why are galaxies spinning?” and “Are the orientations of galaxies correlated?” These questions have been the main motivator for observational studies of galaxy alignments during the 20th century (described in detail in the historical overview of the subject by Joachimi et al. 2015). However, no consensus was reached on the existence of of alignments between galaxy shapes or spins. For instance, some studies have claimed that cluster galaxies are preferentially oriented towards the bright central galaxy, whereas others found no evidence for this. Much of this controversy can be attributed to the quality of the data, but differences in observational techniques can play a role as well. Weak gravitational lensing as a cosmological tool provided new impetus for the study of galaxy shapes and alignments in the 21st century. Weak lensing measures coherent distortions to the images of background sources that can be mimicked or hidden by galaxy shape alignments.

Galaxy shapes and orientations can be measured using different approaches. For instance, one can consider the region of a galaxy above a given surface brightness and determine its ellipticity and position angle. In particular, early studies, based on photographic plates, tend to fall into this category because the measurement involved determining the semi-major and semi-minor axis above some surface brightness limit. Even though the resulting ellipticity might be biased, due to the particular choice of surface brightness, the estimate of the position angle from these early studies is expected to be robust, provided the galaxy is much larger than the size of the point spread function (PSF). The adopted surface brightness limit, which may itself be determined by the depth of the observations, can affect the result because low surface brightness features, such as discs or even tidal tails, only show up if the data are sufficiently deep. Figure 1 highlights this problem: we show an example of a well resolved galaxy observed by the Hubble Space Telescope (HST) as part of the COSMic evOlution Survey (COSMOS, (Scoville et al., 2007)). The different isophotes that are indicated show how the morphology of real galaxies varies dramatically as a function of surface brightness level. For reference the green ellipse in Figure 1 corresponds to the best fit single Sérsic model (Sersic, 1968) to the galaxy image.

Figure 1. An example of a well-resolved galaxy observed as part of the COSMOS survey. The dark blue, light blue and red contours mark isophotes that match 5%, 20% and 50% of the peak flux level, respectively. The morphology clearly varies with surface brightness and the measured shape will be a strong function of the isophotal limit that is adopted. For comparison the green ellipse indicates the ellipticity of the best fit single Sérsic model.

Early observational studies focused on understanding the physical origin of the alignments of galaxy positions and shapes, but the first detections of the weak lensing signal by large-scale structure (Bacon et al., 2000, Kaiser et al., 2000, Van Waerbeke et al., 2000, Wittman et al., 2000) spurred new interest in the topic because of the potential of weak gravitational lensing as a tool to study the dark matter distribution in the Universe. Weak gravitational lensing seeks to exploit the alignment in observed galaxy shapes caused by the deflection of light by gravity en route from the source galaxy to the observer. What makes weak gravitational lensing particularly interesting is that the observed galaxy alignments can in principle be used to reconstruct the projected mass distribution or to study the statistics of the large-scale structure (Takada & Jain, 2004, Hoekstra & Jain, 2008, Munshi et al., 2008). We will refer to the alignments of galaxy shapes caused by galaxy formation and evolution as intrinsic alignments to differentiate them from alignments sourced by gravitational lensing which we will call cosmic shear.

For this application we need accurate estimates for both the ellipticity (also referred to as the third flattening) and orientation of the galaxies, which are typically expressed as

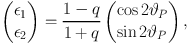(1)

where є_i, with i = 1,2, are the two ellipticity components, q = b / a is the ratio (0 ≤ q ≤ 1) of the estimated semi-minor and semi-major axes, or axial ratio in short, and ϑ_P is the position angle with respect to some reference axis. The factors of 2ϑ_P come from the spin-2 nature of ellipticity due to the symmetry of an ellipse under 180^∘ rotation. Alternatively one can use complex notation, such that є = є₁ + iє₂ or є = |є|e^2iϑ_P. If observed galaxy images are randomly oriented, the ensemble average over galaxies ⟨є_i⟩ = 0.

The differential deflection of light rays by the intervening large-scale structure distorts the images of distant galaxies, resulting in apparent alignments of the observed shapes. To leading order, i.e. in the weak lensing limit, the effect is to change є^s, the intrinsic (or unlensed) ellipticity of a galaxy, to an observed value (Schneider & Seitz, 1995):

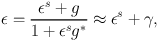(2)

where the asterisk denotes the complex conjugate and g is the reduced shear, which is related to the weak lensing shear γ and convergence κ through g = γ / (1 − κ). In the weak lensing regime, we assume that g ≈ γ. A brief introduction to the topic is given in Joachimi et al. (2015), which also lists references to more thorough discussions of gravitational lensing. The above approximation is only true when we take an ensemble average over many galaxies, for individual galaxies there is an additional term of the same order of magnitude. This term is not relevant for the topics covered in the rest of the paper, see Bartelmann & Schneider (2001) for more detail. Note that the above formalism highlights the usefulness of expressing the ellipticity and shear in complex notation.

The measurement of the weak lensing signal involves the correlation, or averaging, of the ellipticity measurements for many galaxies because the typical lensing-induced change in ellipticity is ∼ 1% or less, much smaller than the average intrinsic galaxy ellipticity. This demonstrates the relevance of intrinsic alignments for lensing studies: only if such alignments vanish, ⟨ є^s ⟩ = 0, is the observed ensemble-averaged ellipticity an unbiased estimator of the lensing shear. Similarly, the galaxy ellipticity correlation function (see Section 3) comprises types of contributions (where i and j here indicate a pair of galaxies and the average is over all pairs):

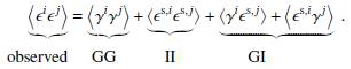(3)

We adopt the following common shorthand notation: GG for the cosmic shear correlation, which is the quantity of interest to constrain cosmological parameters, II indicates the correlations between intrinsic ellipticities, and GI denotes correlations between the shear for one galaxy and the intrinsic ellipticity of the other. In principle one of the GI terms should vanish if foreground and background galaxies can be cleanly separated because the lensing of light from galaxies should not correlate with the intrinsic ellipticity of more distant galaxies.

If the spurious contributions to cosmic shear caused by intrinsic galaxy alignments are significant compared to the statistical errors of the survey then a naive analysis, which ignores the impact of such alignments, will produce biased estimates of cosmological parameters. Although current work indicates that the intrinsic alignment signal is too low to have affected the conclusions of early cosmic shear studies, it is also clear that we can no longer ignore this astrophysical source of bias (Heymans et al., 2013) and that it will be a dominant limitation for future projects, unless we can account for intrinsic alignments in the analysis.

Although the existence of intrinsic alignments has now been firmly established for luminous red galaxies (LRGs; (Mandelbaum et al., 2006a, Hirata et al., 2007, Okumura et al., 2009, Joachimi et al., 2011, Singh et al., 2014)), current observational constraints are not sufficient to correct future cosmic shear surveys (Laszlo et al., 2012, Kirk et al., 2013, Kirk et al., 2012). Further progress relies on making observations with sufficient redshift precision and spatial coverage to inform models of intrinsic alignments, or calibration using the cosmic shear survey data themselves (Bernstein, 2009, oachimi & Bridle, 2010). Importantly, as we will discuss in more detail below, the intrinsic alignment estimates themselves have to be closely linked to the shear measurements in terms of shape measurement, galaxy populations and observational strategy. A further complication is that the source and strength of galaxy alignment depends on galaxy type for reasons described in detail below and treated extensively in Kiessling et al. (2015). Although one can attempt to restrict the analysis to a particular type of galaxy, the source sample typically comprises a mix of galaxies thus mixing possible alignment mechanisms, complicating the analysis (see Joachimi et al. 2015 for more detail). We have been fortunate so far that our knowledge of intrinsic alignments, combined with the size of the observed signal, has kept pace with requirements for cosmic shear surveys to remain unbiased (Heymans et al., 2013). As powerful next generation surveys become available, their reduced statistical error will require a new level of accuracy in quantifying systematic effects such as intrinsic alignments. The observation of galaxy alignments will remain an important topic as we demand more precise measurements over a wider range of scales and redshifts for all types of galaxies.

In this review we focus on observations of the intrinsic alignments of galaxies, their impact on cosmic shear measurements and possible mitigation strategies. For a general introduction and historical review of the subject we refer the reader to Joachimi et al. 2015, which summarises the basic concepts and highlights the most important developments in theory, modelling and observations. A detailed discussion of the physical theories used to model alignments on a range of scales is presented in our companion paper Kiessling et al. (2015), which also reviews intrinsic alignment studies conducted through simulations, thus representing the theoretical counterpart of this more observationally-oriented review.

This review is structured as follows: In Section 2 we discuss how galaxy alignments are measured. The main statistics that are used to quantify the galaxy shape alignment signal are reviewed in Section 3. The most important observations of shape alignment on linear and quasi-linear large scales are discussed in Section 4 and details of environmentally-dependent correlations are reviewed in Section 5. In Section 6 we demonstrate the impact that intrinsic alignments can have on attempts to infer cosmological parameters from cosmic shear surveys as well as outlining the most effective ways to mitigate this impact. We summarise in Section 7 and discuss the outlook for future observations of galaxy shape alignments.