


According to our current understanding, we can distinguish between two types of alignments. In the case of late-type (disc) galaxies the alignments of the angular momenta are believed to play the most important role, whereas the orientation of early-type (elliptical) galaxies is thought to be largely determined by the build-up of the large-scale dark matter distribution that surrounds them. See Joachimi et al. (2015) for a general overview of these mechanisms and Kiessling et al. (2015) for a detailed discussion.
Although the physical processes at play determine the strength of the alignment as a function of separation, the method used to quantify the alignment signal plays an important role as well. Whether or not this is an issue depends on the scientific question that one wishes to address.
In Section 2.1 we consider the measurement of galaxy orientations, concentrating on observing galaxy spin alignment in Section 2.2. We then cover the measurement of galaxy shapes in Section 2.3, including discussion of some common methods. Prominent systematic effects in shape measurement studies are described in Section 2.3.1 and some specific conclusions on the measurement of galaxy shapes with the aim of mitigating intrinsic alignments in cosmic shear surveys are made in Section 2.3.2.
Naturally, a critical ingredient in weak lensing studies is the measurement of the alignment of the shapes of galaxies. This measurement is quantified by a galaxy's ellipticity and position angle with respect to some local coordinate system. In this context it is interesting to note that an appropriate observation of an alignment of position angles (regardless of ellipticity) will be sufficient to imply that weak lensing measurements are contaminated by galaxy intrinsic alignments. However, an accurate estimate of the level of contamination still requires knowledge of the distribution of ellipticities, which itself may vary locally (as the mix of galaxy types depends on environment). Hence, while early studies that focused only on the orientations of galaxies have been useful, a successful correction of the intrinsic alignment signal in weak lensing studies requires more information.
Studies using orientations rather than shapes also suffer a particular ambiguity: what is the orientation of nearly round galaxies? For a fixed total signal-to-noise galaxy detection, the uncertainty on the galaxy orientation is smallest for highly flattened galaxies and largest for those that are nearly round. The way this problem is dealt with in practice varies, with some studies ignoring it entirely (e.g., Pereira & Kuhn, 2005, Agustsson & Brainerd, 2006, Faltenbacher et al., 2007, Faltenbacher et al., 2009, Okumura et al., 2009, Li et al., 2013a). Since ignoring this issue will tend to dilute any alignments by adding random noise, that simple strategy is in fact a valid approach when trying to simply detect alignments. However, ignoring the dilution of the orientation correlations due to nearly round galaxies in the sample complicates both the theoretical interpretation of the results and also the comparison with results from other samples (which may have different intrinsic shape distributions and/or levels of noise).
Another approach is to exclude galaxies with axial ratios b/a ∼ 1.0 on the grounds that their position angles are meaningless (Niederste-Ostholt et al., 2010). Again, such exclusion does not cause any problem for claiming a detection of intrinsic alignments but this comes at the cost of the interpretation of the measured alignments in terms of a theoretical model being complicated by selection biases. Smargon et al., (2012) give a simple example of a mathematical model for including uncertainties in position angles in real data in a theoretical model for alignments. This is done in the context of cluster alignments, but the same argument is valid for galaxy alignments. Unfortunately, in this model, all galaxies are assumed to have, on average, the same position angle uncertainty; if alignments vary with shape (just as the position angle uncertainties do), then this prescription would no longer be applicable. An alignment estimate based on shape measurements does not suffer from these problems as there is no ambiguity in assigning a small ellipticity to a nearly circular galaxy, though, of course, signal-to-noise may be lower for galaxies with small ellipticities in real, noisy data.
Looking beyond position angles, measurements of the alignments between the angular momenta of galaxies may provide unique insights into the formation of disc galaxies, especially on the origin of the observed galactic angular momentum. The ellipticities of disc galaxies are the result of the projection of their orientation with respect to the observer, combined with any intrinsic ellipticity due to not being a perfectly circular disc. If we assume that disc galaxies obtain their angular momentum from tidal torquing, they should spin around their minor axis. Inclination angle, ξ, refers to the angle between the observer's line of sight and the symmetry axis of a disc galaxy. Position angle, ϑP, refers to the angle between the major axis of the ellipse of a projected galaxy image and the north of some coordinate system. Assuming the circular, infinitely thin-disc approximation and measurements of both of these angles, the components of the unit spin vector are given by
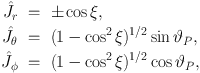 |
(4) (5) (6) |
where r, θ and φ are spherical polar coordinates with an origin at the galactic centre and r pointing along the line of sight. The spatial correlation of the spin axes can then be written as
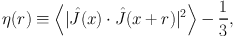 |
(7) |
where we are averaging over the position, x, of all galaxy pairs separated by a distance r (Lee, 2011). The value of 1/3 is subtracted since it is the value of the ensemble average when there is no correlation.
The direction of the galactic angular momentum (i.e. the spin axis of the galaxy) is expected to be connected to the properties of the underlying dark matter halo. If the correlation between angular momentum and the distribution of dark matter is retained after galaxy formation, then the correlation of the density field, which can be predicted using numerical simulations (Kiessling et al. 2015), should be replicated in correlations of galaxy orientation. Alternatively, a lack of correlation may provide insights into the processes that allow galaxies to form large rotating discs. For instance, van den Bosch et al. (2003) showed how pre-heating of the intergalactic medium unbinds baryons from their dark matter haloes, which may lead to misalignments between the angular momentum of the gas and the dark matter.
For studies that seek to correlate galaxy spins, a fundamental observational problem is the “deprojection” of the observed galaxy shape and the accurate determination of the direction and sign of the spin vector. Using a galaxy's observed axial ratio, q, and position angle, ϑP, it is possible to determine the unit spin vector, Ĵ, up to a two-fold ambiguity in the sign of the spin i.e. clockwise or anti-clockwise (Lee, 2011). Early works (Lee & Pen, 2000) assumed a thin disc geometry in this calculation. In reality discs have finite thickness which must be accounted for to make an accurate estimate. This involves the assumption of an intrinsic flatness parameter which depends on galaxy morphological type (Haynes & Giovanelli, 1984, Lee & Erdogdu, 2007). One simplistic way to avoid deprojection uncertainties would be to use only galaxies which are edge-on or face-on to the observer (Trujillo et al., 2006, Slosar & White, 2009), however this greatly reduces the available number density in a given sample.
If the right observations are available, it is possible to lift the degeneracy in the sign of the spin of a galaxy. The presence of dust lanes (Colina & Wada, 2000) or the use of kinematic data (Obreschkow et al., 2015) can both be used to determine clockwise or anti-clockwise spin. In the absence of such additional information, authors have adopted a number of strategies. Some assumed the sign of the spin of each galaxy was completely independent (Kashikawa & Okamura, 1992), some assumed all galaxies had the same spin direction (Lee & Erdogdu, 2007) and some attempted a statistical approach that combined distributions which assumed all spin signs were positive or negative into a single, corrected, distribution (Varela et al., 2012). Each approach resulted in a serious decrease in the available information. Future mapping of the neutral hydrogen density with 21cm measurements using the Square Kilometre Array (SKA) will be able to deliver unambiguous measurements of the spin sign as well as measurements of angular momentum accurate to 3−5% for millions of disc galaxies (Obreschkow & Glazebrook, 2014, Obreschkow et al., 2015).
Reproducing the observed finite thicknesses and sizes of disc galaxies has been a challenge for numerical hydrodynamic simulations, because the results are sensitive to the implementation of the various processes of baryonic physics. Consequently it is not clear whether the predicted shapes can be compared to observations. On the other hand, the prediction for the orientation of the spin axis should be more robust. Measurements of the alignments of the spin axes of disc galaxies may therefore be useful to provide insights to the process that aligns the angular momentum. The usefulness of such observations for weak lensing studies, in particular to correct cosmic shear measurements, is limited because this would require a prediction for the galaxy shapes as well. We therefore focus for the remainder of this section on the measurement of galaxy shapes.
The practical measurement of galaxy shapes is fundamental to both weak gravitational lensing studies and much of the intrinsic alignment literature. Galaxy shapes can be quantified using various approaches and a wide range of tools have been used for intrinsic alignment measurements in the past. In the case of cosmic shear, the galaxies for which shapes are measured are typically faint and have sizes that are comparable to that of the PSF. The effect of the PSF is twofold: (i) because it has a finite size, it leads to observed images that are rounder; (ii) the PSF is typically anisotropic, resulting in alignments in the observed images. Measuring accurate shapes for the source galaxies is challenging, and understanding the limitations and improving shape measurement algorithms has been an area of active research (see e.g. results of the Shear TEsting Programme (STEP) and GRavitational Lensing Accuracy Testing (GREAT) challenges, Heymans et al. 2006, Massey et al. 2007, Bridle et al. 2010, Kitching et al. 2012, Mandelbaum et al. 2014, and references therein). As cosmic shear studies are the main driver for current research on this topic, we focus the discussion on the algorithms used to measure the lensing signal.
One approach, which is gaining popularity thanks to increases in computing power, is to fit a parametric model to the observed surface brightness distribution. In the case of weak lensing studies the initial model is sheared and convolved with the PSF. The model parameters are varied until the resulting image best matches the observations, which yields an estimate for the ellipticity; examples are lensfit (Miller et al., 2013) and im3shape (Zuntz et al., 2013). However, the choice of suitable models is not straightforward because galaxies can have complex morphologies. If the model is too rigid, the resulting shapes will be biased (Voigt & Bridle, 2010, Melchior et al., 2010), but if the model is too flexible, the shape will be biased too, because of noise in the image (Refregier et al., 2012, Kacprzak et al., 2012, Melchior & Viola, 2012). Forward modelling requires many calculations and is therefore computationally expensive when many parameters are included. For this reason model-fitting algorithms have not yet been extensively used, although lensfit was employed to analyse the Canada France Hawaii Telescope Lensing Survey data (CFHTLenS; Heymans et al., 2012b). An additional advantage of these forward modelling approaches is that various instrumental effects can be incorporated into a Bayesian framework, with priors imposed on the various model parameters. However, accurate priors are needed, particularly for faint galaxies and such information is not always available.
Alternatively, galaxy shapes can be quantified using the moments of the surface brightness distribution of a galaxy. The quadrupole moments Qij are defined as
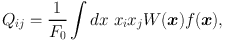 |
(8) |
where x denotes the two-dimensional position on the sky (with i,j∈ {1,2} denoting each dimension), where f(x) is the surface brightness of the galaxy image and W(x) is a weight function. Note that the centre is chosen such that the weighted dipole moments vanish and we normalise using the weighted monopole moment, F0 (which corresponds to the flux in the case of unweighted moments). When measuring moments from real data, a weight function is needed to suppress the contribution of noise to the moments. In terms of the signal-to-noise ratio, the optimal choice for the weight function is to match it to the galaxy image. However, other choices can be made to reduce the sensitivity to possible sources of bias, such as the uncertainty in the underlying ellipticity distribution. Similar to the model fitting approach, where models used are often brighter in the center and deviations from the model there affect the fit a lot because of the high signal-to-noise ratio, the effect of the weight function in Equation (8) is to give more weight to the central (brighter) regions of the galaxy.
As we discuss below, moments are not only a useful way to quantify shapes; they can also, as was shown in Massey et al., (2013), give insights into the relative importance of various observational biases, such as those caused by the PSF. The observed surface brightness distribution is the convolution of the true galaxy image and the PSF. For both cosmic shear and intrinsic alignment studies we wish to infer the moments (or shapes) of the former. In the case of unweighted moments the correction for the PSF is straightforward as
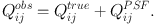 |
(9) |
The galaxy ellipticity, or third flattening, can be expressed in terms of the corrected unweighted quadrupole moments (i.e. adopting W = 1) through:
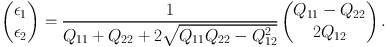 |
(10) |
Noise in real data prevents the use of unweighted moments. However, the need to use weighted moments leads to new complications: the correction for the PSF (and weight function itself) involves knowledge of higher order moments, which themselves are affected by noise. Limiting the expansion in moments is similar to the model bias mentioned above. Although Equation 10 can be used to compute the ellipticity from the best-fit parametric model, moment-based methods tend to make use of the polarisation, also called the third eccentricity or distortion (Bernstein & Jarvis, 2002), given by:
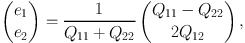 |
(11) |
which avoids the square root of a combination of moments in the denominator. The two definitions are related through e = 2є / (1 + |є|2). A discussion of these quantities, and their probability distributions is presented in Viola et al. (2014).
Kaiser et al., (1995) considered the first-order change in the polarisation, δ ei, induced by a small constant gravitational shear, for an arbitrary weighting function W(x), and found that this can be expressed as δ ei = Pijγ γj, where the indices denote the two components of the ellipticity and shear, respectively, and the Einstein summation convention is assumed. The polarisability tensor Pijγ depends in a rather complicated manner on the morphology and surface brightness distribution of the galaxy. However, it can be directly measured for each individual galaxy, and thereby can be used to calibrate the polarisation measurements: the average of ei / Pijγ in a particular patch of sky will be directly proportional to the gravitational shear γj in that region. This can therefore be used to construct an unbiased estimate of the gravitational shear. This is why image simulations are used to not only compare the performance of algorithms (e.g. Heymans et al., 2006, Bridle et al., 2010, Kitching et al., 2012, Mandelbaum et al., 2014), but also to calibrate algorithms (e.g. Miller et al., 2013, Hoekstra et al., 2015). The various definitions for the shapes of galaxies are often used loosely in the literature, which is important to keep in mind when comparing published results.
2.3.1. Shape measurement systematics
A bright, isolated galaxy which subtends a large angle on the sky would be an ideal candidate for shape estimation. However, galaxies are clustered and much of the cosmological signal comes from galaxies near dense regions. Hence, most galaxies are not isolated but “blended” with other sources and the shape measurements are compromised (see Hoekstra et al. 2015, Dawson et al. 2014). This is particularly important if we wish to study intrinsic alignments as a function of environment.
For example, Hao et al., (2011) showed that significant detections of satellite galaxy alignments using some shape measurement methods can be attributed to contamination by neighbouring galaxies. Satellite galaxies are particularly prone to suffer this effect, being usually relatively dim with many bright neighbours. In addition there is an intra-cluster light contribution from stars bound to the cluster after being stripped from member galaxies (Zwicky, 1951, Gonzalez et al., 2007, Burke et al., 2012, Guennou et al., 2012, Adami et al., 2013, Presotto et al., 2014). The amount of bias will depend on the shape measurement method (Hao et al., 2011), with isophotal measurements being particularly sensitive, see discussion of Figure 1 above. Indeed, the papers that report detections of satellite alignments have been made using isophotal measurements (Pereira & Kuhn, 2005, Agustsson & Brainerd, 2006, Yang et al., 2006, Faltenbacher et al., 2007) which weight the outskirts of galaxies more strongly than weak lensing-optimised measurements. The later results, which report no significant alignment (Hao et al., 2011, Hung & Ebeling, 2012, Schneider et al., 2013, Chisari et al., 2014, Sifón et al., 2015), are therefore less prone to these effects. A conclusion to the same effect was reached by Schneider et al., (2013).
The correction for smearing by the PSF is critical in any lensing analysis: the finite size of the PSF leads to rounder images and observed ellipticities lower than the true values. This bias is commonly referred to as multiplicative bias as it merely scales the amplitude of the signal. However, due to (inevitable) misalignments of optical elements and atmospheric turbulence, the PSF is never perfectly round but tends to have a preferred direction, which may vary spatially and with time. This leads to an additional signal (therefore referred to as additive bias), which can mimic the cosmological or intrinsic alignment signal. For this reason cosmic shear studies take great care in characterising the PSF and quantifying any residual systematics (see e.g. Heymans et al., 2012b). Similar rigour is required for accurate measurements of intrinsic alignments. Most recent results (see Section 4) are based on weak lensing pipelines, but we note that this is not the case for older studies of intrinsic alignments.
The change in observed shape depends on the size of the galaxy relative to the PSF. How various biases propagate was studied in detail in Massey et al., (2013). If the PSF is sufficiently well understood then it can be used to correct the observed shapes either using the observed moments of the surface brightness distribution or by convolving galaxy models with the PSF model. A complication is that the PSF varies in time, due to turbulence in the atmosphere (e.g. Heymans et al., 2012a) or variations in the thermal and gravitational load on the optical elements. However, if a sufficiently large number of stars are visible in the field-of-view, these can be used to quantify the spatial variation of the PSF (Hoekstra, 2004, Jain et al., 2006). The PSF is not the only instrumental source of bias, imperfections in the detector can also affect the observed shapes. In the case of space-based observations, radiation damage causes charge traps leading to charge-transfer inefficiency during read-out (e.g. Rhodes et al., 2010, Massey et al., 2014). This produces charge trails, which result in alignments of the observed images. This is less relevant for ground-based observations where the brighter sky fills the charge traps but other effects persist, including charge-induced pixel shifts (Gruen et al., 2015), the brighter/fatter effect for individual charge wells (Antilogus et al., 2014) and others.
2.3.2. Intrinsic alignment measurements and cosmic shear
We discuss the issue of mitigating the impact of intrinsic alignments on cosmic shear measurements in more detail in Section 6. Note for now that in the typical situation all terms in Equation (3) are relevant, hence the observed signal is a combination of the lensing signal itself and the II and GI contributions. We have discussed how shape measurement can depend on details of the algorithm deployed; accurately accounting or correcting for the contribution of the intrinsic alignment signal in a cosmic shear measurement therefore requires that the same shape measurement algorithm is used for both the weak lensing measurement and the estimate of the alignment signal. This condition may be trivially satisfied if the intrinsic alignment signal is determined from the cosmic shear survey itself, but one can also imagine scenarios where the intrinsic alignment signal is modelled using external data. Attempts to employ intrinsic alignment measurements acquired using different data or a different shape measurement algorithm should only be undertaken with great care.
For instance, for low redshift galaxies the shear is low and the correlations between galaxy shapes are dominated by the II term. As such galaxies are bright and large compared to the PSF, their shapes can be measured reliably using deep modern observations. A limitation is that the number of sufficiently large and bright galaxies is small, giving rise to a large shot noise. However, a more serious concern is that it is not clear how to relate such measurements to predictions for the intrinsic alignment signal for galaxies at higher redshifts. As shown in Section 1, the estimated galaxy shape depends on the weight function applied to the galaxy light profile, which might differ for a well-resolved low-redshift observation and a poorly-resolved high-redshift observation of two very similar galaxies. A further complication is that, even if a robust shape measurement method can be found, which can measure shapes well regardless of redshift, the mix of galaxy types and properties may evolve and the intrinsic alignments themselves may vary with time.
Therefore direct measurements of the alignments of distant galaxies are needed. In fact, such studies will have to use the actual cosmic shear survey data. This naturally implies that the requirements on the accuracy of the shape measurements are similar, including a careful correction for the PSF. Moreover, to be able to extract the intrinsic alignment contributions with sufficient precision, good photometric redshift information is required. As the lensing kernel is broad in redshift, the required precision of photometric redshifts for the next generation of cosmic shear surveys is actually driven by our desire to model intrinsic alignments (Amara & Réfrégier 2008, Joachimi & Bridle 2010, Laszlo et al. 2012 see Section 3.3 for more details on the importance of redshift precision).