


We can assume that the stellar mass surface density Σ⋆(r) is proportional to the luminosity surface density, which in galaxies is well measured by CCD infrared photometry. Radial variations of the M⋆ / L ratio exist and often are astrophysically relevant, but rarely they play a role in the determination of the mass profile of galaxies.
The total galaxy luminosity is related to its stellar content, hence, the direct approach to derive the galactic mass in stars by modelling their spectral energy distribution in terms of age, metallicity, initial mass function of the stellar component. This modelling, pioneered by Tinsley (1981), is performed by the well-known stellar population synthesis technique. The SED of a galaxy, selected colour indices and absorption lines are all reproduced by a theoretical models calculated under different assumptions regarding the above physical quantities. In practice, the exercise is not straightforward because degeneracies among age, metallicities, IMF and dust content, to name some, do arise and different combinations of the former quantities yield to very similar SEDs.
Bell and de Jong (2001) found rather simple relationships between mass-to-light ratios and certain colour indices. In detail, they investigated a suite of spectrophotometric spiral galaxy evolution models that assumed a Salpeter Initial Mass Function, an exponentially declining star formation rate and a current age of 12 Gyr and found that the stellar mass to light ratios correlate tightly with galaxy colours (see also Bell et al. 2003).
The important stellar mass-to-light ratios in the Spitzer 3.6 µm band (Υ⋆3.6 µm) and in the K-band (Υ⋆K) have also been derived by constructing stellar population synthesis models, with various sets of metallicity and star-formation histories (see Oh et al. 2008, de Blok et al. 2008).
We have
 |
(27) |
The values of the galaxy stellar masses as derived from their SEDs have been compared with those obtained by other methods. Grillo et al. (2009) investigated a sample of ellipticals with Einstein rings from which they derived the total projected mass (dominated by the stellar component) and, from the latter, the total mass of the spheroid. Then, by using the SDSS multicolour photometry they fitted the galaxy spectral energy distributions (SEDs) by means of composite stellar-population synthesis models of Bruzual and Charlot (2003) and Maraston (2013) and obtained the photometric mass of the stellar spheroid. The two different mass estimates agreed within 0.2 dex (see also Tiret et al. 2011).
Salucci et al. (2008) have estimated kinematically the disk mass from the rotation curve of 18 spirals of different luminosity and Hubble types and have compared them with the values obtained by fitting their SED with spectro-photometric models. They found Mpho ∝ Mkin1.0 ± 0.1 with a r.m.s. of 40% suggesting that photometric and kinematical estimate of the masses of the stellar galaxy disks are statistically consistent.
We have to caution about one consequence of the found disagreement of about 0.15 dex among the dynamical and the spectro-photometric estimates. This value is small to affect existing color stellar mass relationships, but it is large if we want to use it for mass modelling purposes. In fact, in spirals, for R < RD, the dark and the luminous components of the circular velocity are of the same order of magnitude Vh ≃ Vd (MD,true / MD,phot)−0.5 and therefore an uncertainty of (100.15 − 1) 100% ∼ 40% on the value of MD,phot jeopardizes the derivation of the DM velocity contribution and even more that of the subsequent DM halo density.
For spiral galaxies there is a reliable method to estimate the disk mass which is immune from the latter uncertainty. We start from the gravitating mass inside Ropt : Mg(Ropt) ≡ G−1 Vopt2 Ropt and ∇, the rotation curve logarithmic slope measured at Ropt: ∇≃ 3.2 (1 − V(2.2 RD) / V(Ropt)). From Persic and Salucci (1990) we have:
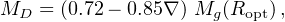 |
(28) |
where the disk mass has uncertainty of 20%.